Weibull分布是最常用于對可靠性數據建模的分布。此分布易于解釋且用途廣泛。在可靠性分析中，可以使用此分布回答以下問題：

· 預計將在老化期間失效的項目所占的百分比是多少？例如，預計將在8小時老化期間失效的保險絲占多大百分比？

· 預計在有效壽命階段有多少次保修索賠？例如，在該輪胎的50,000英里有效壽命期間預計有多少次保修索賠？

· 預計何時會出現快速磨損？例如，應將維護定期安排在何時以防止發動機進入磨損階段？

Weibull分布可以對右偏斜數據、左偏斜數據或對稱數據建模。因此，分布可用來評估不同應用（包括真空管、電容器、滾珠軸承、繼電器和材料強度）的可靠性。Weibull分布還可以對遞增、遞減或固定故障函數建模，并允許使用該模型描述項目壽命的任何階段。

Weibull分布參數和故障函數之間的關系

通過調整Weibull分布的形狀參數β，可以對許多不同壽命分布的特征建模。

1. 0<β<1

早期失效發生在產品壽命的初始階段。這些失效可能會迫使產品進入“老化”階段以降低初期失效的風險。

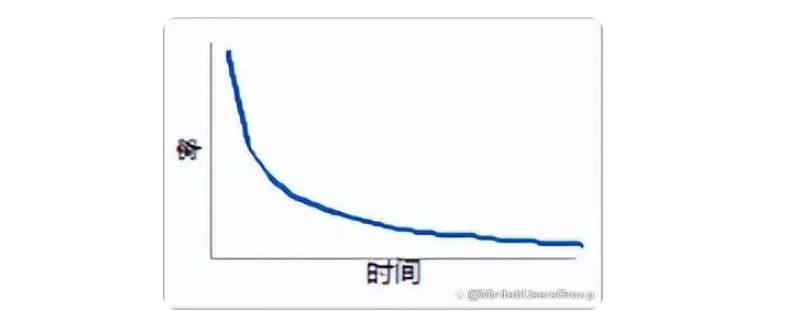
故障函數：初始失效率很高，隨著時間的推移會逐漸降低（“浴盆”形狀故障函數的第一部分）。

2. β=1

失效率保持恒定。隨機失效，失效的原因有多種。對產品的“使用壽命”建模。

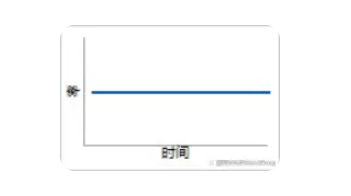
故障函數：失效率在產品壽命期間保持恒定（“浴盆”形狀故障函數的第二部分）

3. β=1.5

早期磨損失效

故障函數：失效率不斷增加，最初增加速度最快

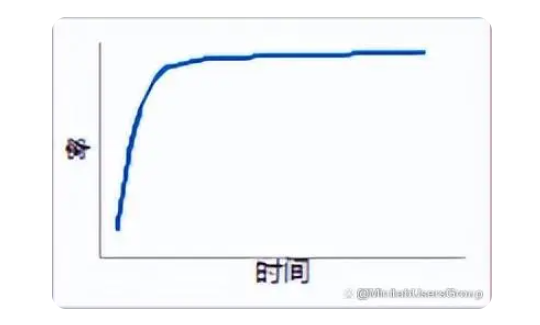
4. β=2

在產品的壽命期間，磨損失效風險不斷增加（當Weibull分布的形狀參數為2時，它被稱為Rayleigh分布。此分布通常用來描述通信工程領域中的測量數據，如輸入回波損耗、調制邊帶注入、載波抑制和RF衰減的測量數據。此分布還廣泛用于電真空設備的壽命檢驗中。）

故障函數：失效率呈線性增加

5. 3≤β≤4

快速磨損失效。當大多數的失效都出現后，對產品壽命的最后時間段建模。

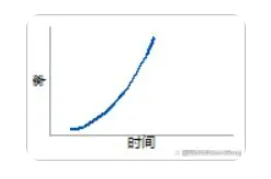
故障函數：失效率快速增加

6. β＞10

非常快的磨損失效。當大多數的磨損失效都出現后，對產品壽命的最后時間段建模。

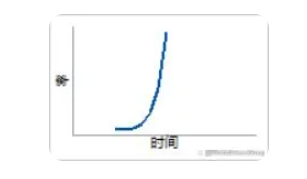
故障函數：失效率增加速度非常快

失效率關于時間的圖形稱為故障圖。產品的失效率隨時間的變化大致可以分為三個階段：

早期故障階段、偶然故障階段和耗損故障階段。基于上面介紹，我們發現根據Weibull分布形狀參數β的不同，這三個階段都可以進行描述，于是就形成了如下的“浴盆曲線”。

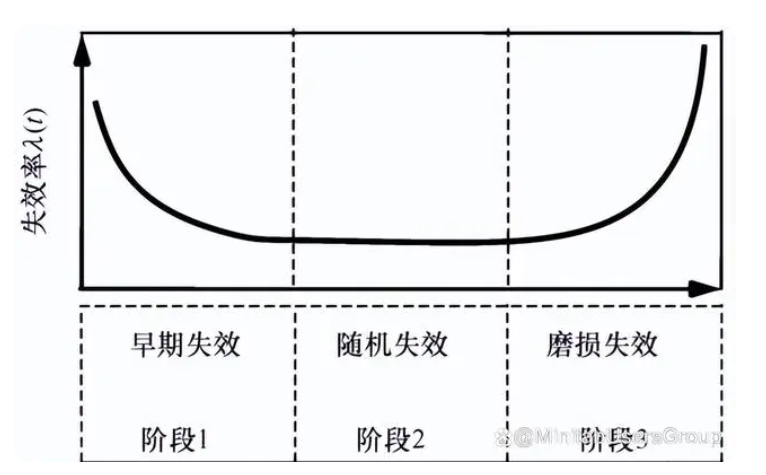
β<1時，失效率遞減，可以描述浴盆曲線的早期故障階段

β=1時，失效率恒定，可以描述浴盆曲線的偶然故障階段

β＞1時，失效率遞增，可以描述浴盆曲線的耗損故障階段

吐槽一下

也可能正是因為Weibull分布看起來很牛，以至于很多朋友把“Weibull”和“可靠性”等價，這其實是有問題的。Minitab中可靠性分析分布其實有11種，而Weibull分布只是其中一種而已，并不是所有壽命數據用Weibull都能擬合的很好。

審核編輯黃宇