三、算法刷題指南
首先要明確的是, 數據結構是工具,算法是通過合適的工具解決特定問題的方法 。也就是說,學習算法之前,最起碼得了解那些常用的數據結構,了解它們的特性和缺陷。
那么該如何在 LeetCode 刷題呢?之前的文章算法學習之路寫過一些,什么按標簽刷,堅持下去云云。現在距那篇文章已經過去將近一年了,我不想說那些不痛不癢的話了,直接說具體的建議:
先刷二叉樹,先刷二叉樹,先刷二叉樹 !
這是我這刷題的親身體會,下圖是我從 2018/10 到 2019/10 這一年的心路歷程:
公眾號文章的閱讀數據顯示,大部分人對數據結構相關的算法文章不感興趣,而是更關心動規回溯分治等等技巧。為什么要先刷二叉樹呢, 因為二叉樹是最容易培養框架思維的,而且大部分算法技巧,本質上都是樹的遍歷問題 。
刷二叉樹看到題目沒思路?根據很多讀者的問題,其實大家不是沒思路,只是沒有理解我們說的「框架」是什么。 不要小看這幾行破代碼,幾乎所有二叉樹的題目都是一套這個框架就出來了 。
void traverse(TreeNode root) {
// 前序遍歷
traverse(root.left)
// 中序遍歷
traverse(root.right)
// 后序遍歷
}
比如說我隨便拿幾道題的解法出來,不用管具體的代碼邏輯,只要看看框架在其中是如何發揮作用的就行。
LeetCode 124 題,難度 Hard,讓你求二叉樹中最大路徑和,主要代碼如下:
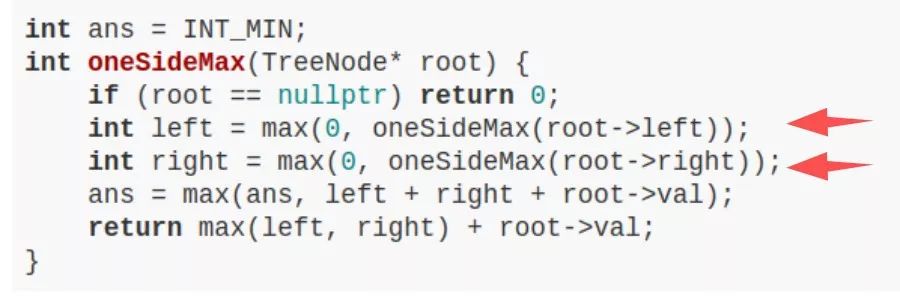
看出來了嗎,這就是個后序遍歷嘛。
LeetCode 105 題,難度 Medium,讓你根據前序遍歷和中序遍歷的結果還原一棵二叉樹,很經典的問題吧,主要代碼如下:
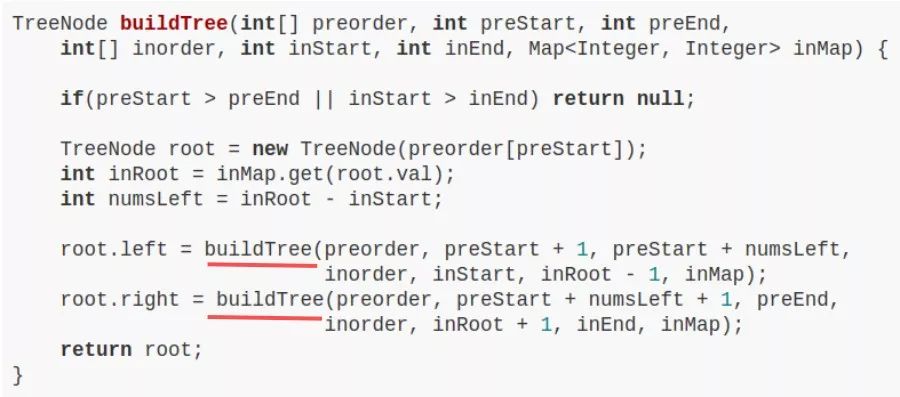
不要看這個函數的參數很多,只是為了控制數組索引而已,本質上該算法也就是一個前序遍歷。
LeetCode 99 題,難度 Hard,恢復一棵 BST,主要代碼如下:

這不就是個中序遍歷嘛,對于一棵 BST 中序遍歷意味著什么,應該不需要解釋了吧。
你看,Hard 難度的題目不過如此,而且還這么有規律可循,只要把框架寫出來,然后往相應的位置加東西就行了,這不就是思路嗎。
剛開始刷二叉樹的題目,前 10 道也許有點難受;結合框架再做 20 道,也許你就有點自己的理解了;刷完整個專題,再去做什么回溯動規分治專題,你就會發現只要涉及遞 歸的問題,都是樹的問題 。
def coinChange(coins: List[int], amount: int):
def dp(n):
if n == 0: return 0
if n < 0: return -1
res = float('INF')
for coin in coins:
subproblem = dp(n - coin)
# 子問題無解,跳過
if subproblem == -1: continue
res = min(res, 1 + subproblem)
return res if res != float('INF') else -1
return dp(amount)
這么多代碼看不懂咋辦?直接提取出框架,就能看出核心思路了:
# 不過是一個 N 叉樹的遍歷問題而已
def dp(n):
for coin in coins:
dp(n - coin)
其實很多動態規劃問題就是在遍歷一棵樹,你如果對樹的遍歷操作爛熟于心,起碼知道怎么把思路轉化成代碼,也知道如何提取別人解法的核心思路。
再看看回溯算法,前文回溯算法詳解干脆直接說了,回溯算法就是個 N 叉樹的前后序遍歷問題,沒有例外。
比如 N 皇后問題吧,主要代碼如下:
void backtrack(int[] nums, LinkedList) {
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
if (track.contains(nums[i]))
continue;
track.add(nums[i]);
// 進入下一層決策樹
backtrack(nums, track);
track.removeLast();
}
/* 提取出 N 叉樹遍歷框架 */
void backtrack(int[] nums, LinkedList) {
for (int i = 0; i < nums.length; i++) {
backtrack(nums, track);
}
N 叉樹的遍歷框架,找出來了吧。你說,樹這種結構重不重要?
綜上,對于算法無從下手的朋友來說,可以先刷樹的相關題目,試著從框架上看問題,而不要糾結于細節問題 。
糾結細節問題,就比如糾結 i 到底應該加到 n 還是加到 n - 1,這個數組的大小到底應該開 n 還是 n + 1 ?
從框架上看問題,就是像我們這樣基于框架進行抽取和擴展,既可以在看別人解法時快速理解核心邏輯,也有助于找到我們自己寫解法時的思路方向。
當然,如果細節出錯,你得不到正確的答案,但是只要有框架,你再錯也錯不到哪去,因為你的方向是對的。
但是,你要是心中沒有框架,那么你根本無法解題,給了你答案,你也不會發現這就是個樹的遍歷問題。
這種思維是很重要的,動態規劃詳解中總結的找狀態轉移方程的幾步流程,有時候按照流程寫出解法,說實話我自己都不知道為啥是對的,反正它就是對了。。。
這就是框架的力量,能夠保證你在快睡著的時候,依然能寫出正確的程序; 就算你啥都不會,都能比別人高一個級別。
四、最后總結
數據結構的基本存儲方式就是鏈式和順序兩種,基本操作就是增刪查改,遍歷方式無非迭代和遞歸。
刷算法題建議從「樹」分類開始刷,結合框架思維,把這幾十道題刷完,對于樹結構的理解應該就到位了。這時候去看回溯、動規、分治等算法專題,對思路的理解可能會更加深刻一些。
-
算法
+關注
關注
23文章
4625瀏覽量
93129 -
數據結構
+關注
關注
3文章
573瀏覽量
40176 -
數組
+關注
關注
1文章
417瀏覽量
25993
發布評論請先 登錄
相關推薦
數據結構與算法分析(Java版)(pdf)
為什么要學習數據結構?數據結構的應用詳細資料概述免費下載
什么是數據結構?為什么要學習數據結構?數據結構的應用實例分析




 數據結構和算法學習筆記(2)
數據結構和算法學習筆記(2)











評論