學習信號時域和頻域、快速傅立葉變換(FFT)、加窗,以及如何通過這些操作來加深對信號的認識。
理解時域、頻域、FFT
傅立葉變換有助于理解常見的信號,以及如何辨別信號中的錯誤。 盡管傅立葉變換是一個復雜的數學函數,但是通過一個測量信號來理解傅立葉變換的概念并不復雜。 從根本上說,傅立葉變換將一個信號分解為不同幅值和頻率的正弦波。 我們繼續來分析這句話的意義所在。
所有信號都是若干正弦波的和
我們通常把一個實際信號看作是根據時間變化的電壓值。 這是從時域的角度來觀察信號。
傅立葉定律指出,任意波形在時域中都可以由若干個正弦波和余弦波的加權和來表示。 例如,有兩個正弦波,其中一個的頻率是另一個的3倍。 將兩個正弦波相加,就得到了一個不同的信號。
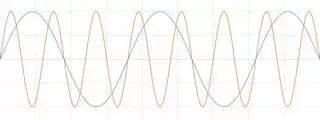
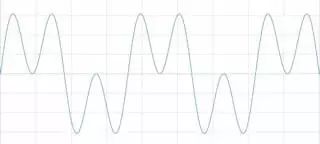
圖1 兩個信號相加,得到一個新的信號
假設第二號波形幅值也是第一個波形的1/3。 此時,只有波峰受影響。
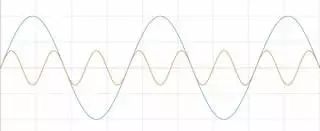
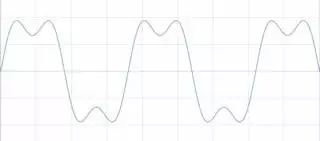
圖2 信號相加時調整幅值影響波峰
假加上一個幅值和頻率只有原信號1/5的信號。 按這種方式一直加,直到觸碰到噪聲邊界,您可能會認出結果波形。
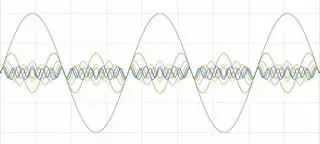
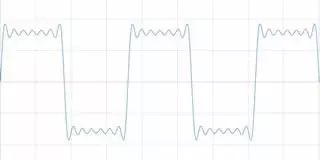
圖3 方波是若干正弦波的和
您創建了一個方波。 通過這種方法,所有時域中的信號都可表示為一組正弦波。
即使可以通過這種方法構造信號,那意味著什么呢? 因為可以通過正弦波構造信號,同理也可以將信號分解為正弦波。
一旦信號被分解,可查看和分析原信號中不同頻率的信號。 請參考信號分解的下列使用實例:
分解廣播信號,可選擇要收聽的特定頻率(電臺)。
將聲頻信號分解為不同頻率的信號(例如,低音、高音),可增強特定頻段,移除噪聲。
根據速度和強度分解地震波形,可優化樓宇設計,避免強烈震動。
分解計算機數據時,可忽略頻率重要性最低的數據,這樣就能更緊湊地利用內存。 這就是文件壓縮的原理。
使用FFT分解信號
傅立葉變換將一個時域信號轉換為頻域信號。 頻域信號顯示了不同頻率對應的電壓。 頻域是另一種觀察信號的角度。
數字化儀對波形進行采樣,然后將采樣轉換為離散的值。 因為發生了轉換,傅立葉轉換在這些數據上無法進行。 可使用離散傅立葉變換(DFT),其結果是離散形式的頻域信號。 FFT是DFT的一種優化實現,計算量較少,但是本質上是對信號的分解。
請查看上圖1中的信號。 有兩個頻率不同的信號。 在該情況下,頻域中就會顯示兩條表示不同頻率的豎線。
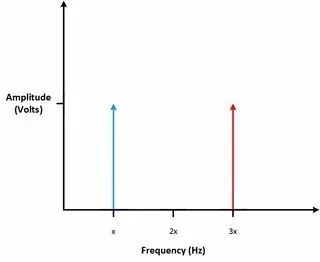
圖4 當相同幅值的兩個正弦波相加,在頻域中就顯示為兩條頻率豎線
原信號的幅值在豎軸上表示。 圖2中有個不同幅值的信號。 頻域中最高的豎線對應于最高電壓的正弦信號。 在頻域里觀察信號,可直觀地看出最高電壓發生在哪個頻率上。
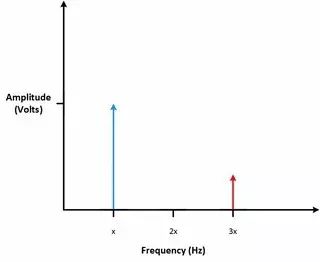
圖5 最高的豎線是幅值最大的頻率
在頻域里也可觀察到信號的形狀。 例如,頻域中方波信號的形狀。 使用不同頻率的正弦波創建一個方波。 即可預見,在頻域中,這些信號都會被表示為一根豎線,每一根豎線都表示組成方波的正弦波。 如頻域中,豎線顯示為一個梯度,就可知道原信號是一個方波信號。
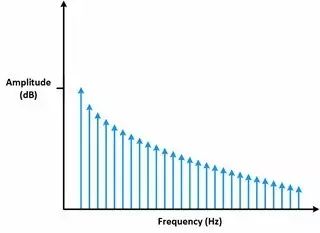
圖6 頻域中表示正弦波的豎線呈現為一個梯度
現實生活中,情況是怎樣的呢? 許多混合信號示波器(MSO)都有FFT功能。 下圖中,你可以觀察到混合信號圖中,方波FFT是如何顯示的。 放大后可觀察到頻域中的尖峰。
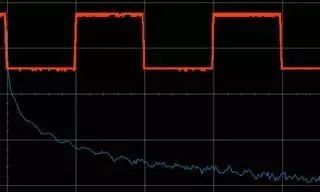
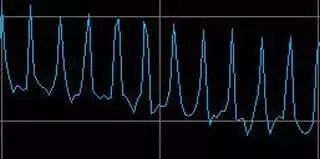
圖7 上圖為原正弦波和FFT,下圖是放大的FFT,可觀察到表示頻率的尖峰
在頻域中觀察信號有助于驗證和發現信號中的問題。 例如,假設有一個輸出正弦波的電路。 可在示波器上查看時域輸出信號,如圖8所示。 看上去沒有任何問題!
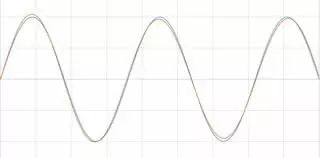
圖8 如果將兩個很相似的波形相加,仍然會得到一個完美的正弦波
在頻域中查看信號時,如果輸出的正弦波頻率穩定,應該只在頻率中顯示為一條豎線。 但是,可以看到在更高的頻率上仍然有一條豎線,表示正弦波并不如觀察到的那么完美。 可嘗試優化電路,去除特定頻率的噪聲。 在頻域中顯示信號有助于發現信號中的干擾、噪聲和抖動。
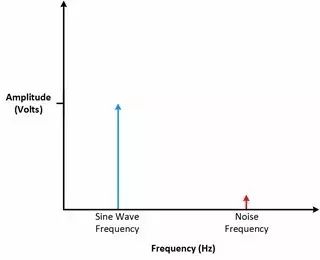
圖9 查看圖8中看似完美的正弦波,可以看出波形中有一個抖動
信號加窗
FFT提供了觀察信號的新視角,但是FFT也有各種限制,可通過加窗增加信號的清晰度。
什么是加窗?
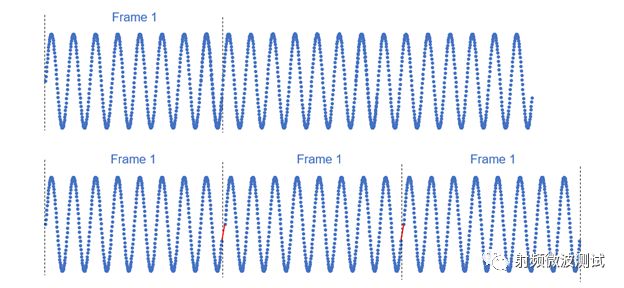
使用FFT分析信號的頻率成分時,分析的是有限的數據集合。 FFT認為波形是一組有限數據的集合,一個連續的波形是由若干段小波形組成的。 對于FFT而言,時域和頻域都是環形的拓撲結構。 時間上,波形的前后兩個端點是相連的。 如測量的信號是周期信號,采集時間內剛好有整數個周期,那么FFT的上述假設合理。
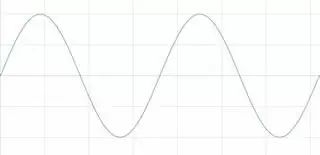
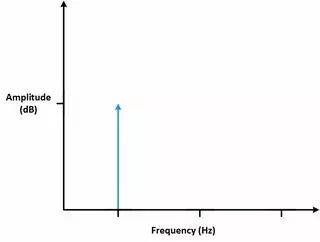
圖10 測量整數個周期(上圖)可以得到理想的FFT(下圖)
在很多情況下,并不能測量到整數個周期。 因此,測量到的信號就會被從周期中間切斷,與時間連續的原信號顯示出不同的特征。 有限數據采樣會使測量信號產生劇烈的變化。 這種劇烈的變化稱為不連續性。
采集到的周期為非整數時,端點是不連續的。 這些不連續片段在FFT中顯示為高頻成分。 這些高頻成分不存在于原信號中。 這些頻率可能遠高于奈奎斯特頻率,在0~采樣率的一半的頻率區間內產生混疊。 使用FFT獲得的頻率,不是原信號的實際頻率,而是一個改變過的頻率。 類似于某個頻率的能量泄漏至其他頻率。 這種現象叫做頻譜泄漏。 頻率泄漏使好的頻譜線擴散到更寬的信號范圍中。
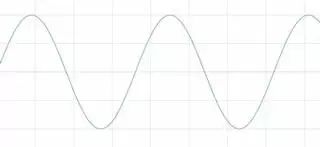
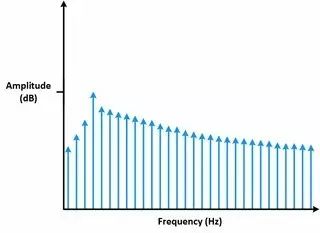
圖11 測量非整數個周期(上圖)將頻譜泄漏添加至FFT(下圖)
可通過加窗來盡可能減少在非整數個周期上進行FFT產生的誤差。 數字化儀采集到的有限序列的邊界會呈現不連續性。 加窗可減少這些不連續部分的幅值。 加窗包括將時間記錄乘以有限長度的窗,窗的幅值逐漸變小,在邊沿處為0。 加窗的結果是盡可能呈現出一個連續的波形,減少劇烈的變化。 這種方法也叫應用一個加窗。
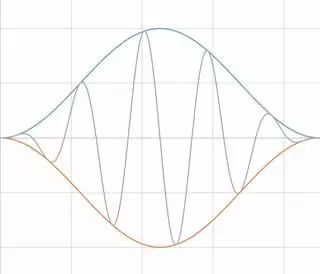
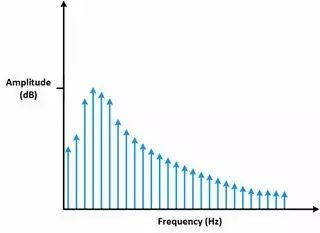
圖12 加窗可盡可能減少頻譜泄漏
加窗函數
根據信號的不同,可選擇不同類型的加窗函數。 要理解窗對信號頻率產生怎樣的影響,就要先理解窗的頻率特性。
窗的波形圖顯示了窗本身為一個連續的頻譜,有一個主瓣,若干旁瓣。 主瓣是時域信號頻率成分的中央,旁瓣接近于0。 旁瓣的高度顯示了加窗函數對于主瓣周圍頻率的影響。 對強正弦信號的旁瓣響應可能會超過對較近的弱正弦信號主瓣響應。
一般而言,低旁瓣會減少FFT的泄漏,但是增加主瓣的帶寬。 旁瓣的跌落速率是旁瓣峰值的漸進衰減速率。 增加旁瓣的跌落速率,可減少頻譜泄漏。
選擇加窗函數并非易事。 每一種加窗函數都有其特征和適用范圍。 要選擇加窗函數,必須先估計信號的頻率成分。
如果您的信號具有強干擾頻率分量,與感興趣分量相距較遠,那么就應選擇具有高旁瓣下降率的平滑窗。
如果您的信號具有強干擾頻率分量,與感興趣分量相距較近,那么就應選擇具有低最大旁瓣的窗。
如果感興趣頻率包含兩種或多種很距離很近的信號,這時頻譜分辨率就非常重要。 在這種情況下,最好選用具有窄主瓣的平滑窗。
如果一個頻率成分的幅值精度比信號成分在某個頻率區間內精確位置更重要,選擇寬主瓣的窗。
如信號頻譜較平或頻率成分較寬,使用統一窗,或不使用窗。
總之,Hanning窗適用于95%的情況。 它不僅具有較好的頻率分辨率,還可減少頻譜泄露。 如果您不知道信號特征但是又想使用平滑窗,那么就選擇Hanning窗。
即使不使用任何窗,信號也會與高度一致的長方形窗進行卷積運算。 本質上相當于對時域輸入信號進行截屏,對離散信號也有效。 該卷積有一個正弦波函數特性的頻譜。 基于該原因,沒有窗叫做統一窗或長方形窗。
Hamming窗和Hanning窗都有正弦波的外形。 兩個窗都會產生寬波峰低旁瓣的結果。 Hanning窗在窗口的兩端都為0,杜絕了所有不連續性。 Hamming窗的窗口兩端不為0,信號中仍然會呈現不連續性。 Hamming窗擅長減少最近的旁瓣,但是不擅長減少其他旁瓣。 Hamming窗和Hanning適用于對頻率精度要求較高對旁瓣要求較低的噪聲測量。
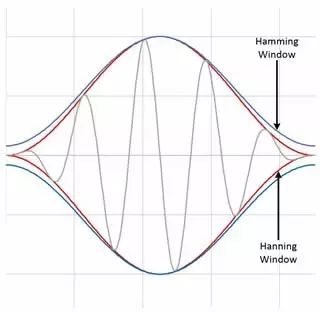
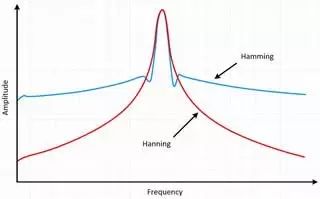
圖13 Hamming和Hanning都會產生寬波峰低旁瓣的結果
Blackman-Harris窗類似于Hamming和Hanning窗。 得到的頻譜有較寬的波峰,旁瓣有壓縮。 該窗主要有兩種類型。 4階Blackman-Harris是一種通用窗,在高90s dB處具有旁瓣抑制功能,有較寬的主瓣。 7階Blackman-Harris窗函數有寬廣的動態范圍,有較寬的主瓣。
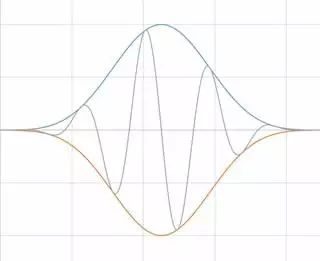
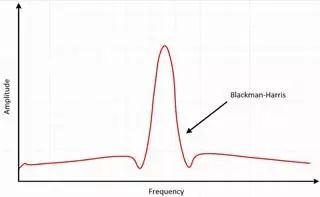
圖14 Blackman-Harris窗的結果是較寬的波峰,旁瓣有壓縮
Kaiser-Bessel窗在幅值精度、旁瓣距離和旁瓣高度之間取得了較好的平衡。 Kaiser-Bessel窗與Blackman-Harris窗類似,對于相同的主瓣寬度而言,較近的旁瓣更高,較遠的旁瓣更低。 選擇該窗通常會將信號泄漏至離噪聲較近的位置。
Flat top窗也是一個正弦波,穿過0線。 Flat top窗的結果是在頻域中產生一個顯著寬廣的波峰,與其他窗相比離信號的實際幅值更近。
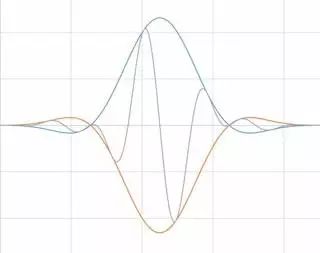
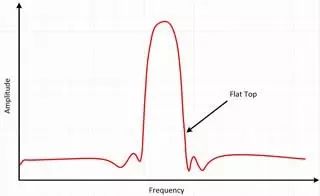
圖15 Flat top窗具有更精確的幅值信息
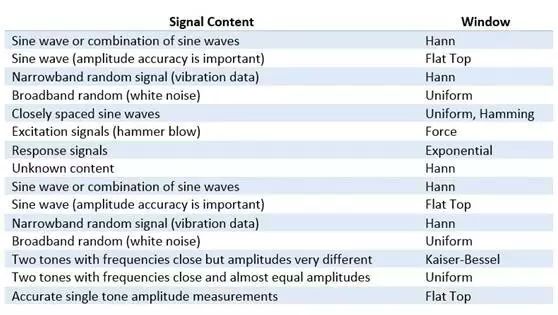
上面列舉了幾種常見的窗函數。 選擇窗函數并沒有一個通行的方法。 下表可幫助您做出初步選擇。 請始終比較窗函數的性能,從而找到最適合的一種窗函數。
總結
所有時域中的信號都可表示為一組正弦波。
FFT變換將一個時域信號分解為在頻域中表示,并分析信號中的不同頻率成分。
在頻域中顯示信號有助于發現信號中的干擾、噪聲和抖動。
信號中如果包含非整數個周期,會發生頻率泄漏。 可通過加窗來改善該情況。
數字化儀采集到的有限序列的邊界會呈現不連續性。 加窗可減少這些不連續部分的幅值。
沒有窗叫做統一窗或長方形窗,因為加窗效果仍然存在。
一般情況下,Hanning窗適用于95%的情況。 它不僅具有較好的頻率分辨率,還可減少頻譜泄露。
請始終比較窗函數的性能,從而找到最適合的一種窗函數。
審核編輯:湯梓紅
-
正弦波
+關注
關注
11文章
643瀏覽量
55400 -
FFT
+關注
關注
15文章
434瀏覽量
59385 -
信號
+關注
關注
11文章
2791瀏覽量
76771 -
時域
+關注
關注
1文章
71瀏覽量
28524 -
頻域
+關注
關注
1文章
87瀏覽量
26288
原文標題:信號基礎:頻域、時域、FFT和加窗
文章出處:【微信號:mcu168,微信公眾號:硬件攻城獅】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
請教各位朋友:時域信號轉FFT后為何要除以樣本數后輸出頻域圖啊?
頻域時域轉換問題
分別用矩形窗、漢寧窗、哈明窗、布萊克曼窗+FFT對信號進行頻譜分析,分析各窗函數對信號FFT變換的影響
基于MATLAB的時域和頻域抽樣計算





 信號基礎:頻域、時域、FFT和加窗
信號基礎:頻域、時域、FFT和加窗
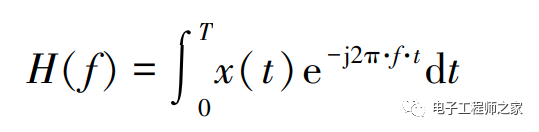













評論