有了全局路徑參考信息,有了局部環(huán)境信息了,有了行為決策模塊輸入的決策信息,下一步自然而然的就要進行運動規(guī)劃,從而生成一條局部的更加具體的行駛軌跡,并且這條軌跡要滿足安全性和舒適性要求。
考慮到車輛是一個具有巨大慣性的鐵疙瘩且沒有瞬間移動的功能,如果僅考慮瞬時狀態(tài)的行駛軌跡,不規(guī)劃出未來一段時間有前瞻性的行駛軌跡,那么很容易造成一段時間后無解。因此,運動規(guī)劃生成的軌跡是一種由二維空間和一維時間組成的三維空間中的曲線,是一種偏實時的路徑規(guī)劃。
運動規(guī)劃的第一步往往采用隨機采樣算法,即走一步看一步,不斷更新行駛軌跡。代表算法是基于采樣的方法:PRM、RRT、Lattice。這類算法通過隨機采樣的方式在地圖上生成子節(jié)點,并與父節(jié)點相連,若連線與障礙物無碰撞風險,則擴展該子節(jié)點。重復上述步驟,不斷擴展樣本點,直到生成一條連接起點到終點的路徑。
PRM
概率路標法 (Probabilistic Road Maps, PRM),是一種經(jīng)典的采樣方法,由Lydia E.等人在1996年提出。PRM主要包含三個階段,一是采樣階段,二是碰撞檢測階段,三是搜索階段。
圖25為已知起點A和終點B的地圖空間,黑色空間代表障礙物,白色空間代表可通行區(qū)域。在采樣階段中,PRM首先在地圖空間進行均勻的隨即采樣,也就是對地圖進行稀疏采樣,目的是將大地圖簡化為較少的采樣點。
在碰撞檢測階段,剔除落在障礙物上的采樣點,并將剩下的點與其一定距離范圍內(nèi)的點相連,同時刪除穿越障礙物的連線,從而構成一張無向圖。
在搜索階段,利用全局路徑規(guī)劃算法章節(jié)介紹的搜索算法(Dijkstra、A*等)在無向圖中進行搜索,從而找出一條起點A到終點B之間的可行路徑。
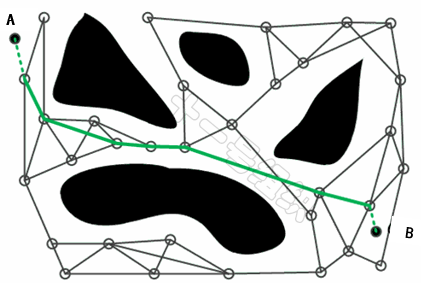
圖27 PRM工作原理示意圖(來源:https://mp.weixin.qq.com/s/WGOUf7g0C4Od4X9rnCfqxA)
算法步驟可以總結(jié)為:
(1)構造無向圖G =(V,E),其中V代表隨機采樣的點集,E代表兩采樣點之間所有可能的無碰撞路徑,G初始狀態(tài)為空。
(2)隨機撒點,并選取一個無碰撞的點c(i)加入到V中。
(3)定義距離r,如果c(i)與V中某些點的距離小于r,則將V中這些點定義為c(i)的鄰域點。
(4)將c(i)與其鄰域點相連,生成連線t,并檢測連線t是否與障礙物發(fā)生碰撞,如果無碰撞,則將t加入E中。
(5)重復步驟2-4,直到所有采樣點(滿足采樣數(shù)量要求)均已完成上述步驟。
(5)采用圖搜索算法對無向圖G進行搜索,如果能找到起始點A到終點B的路線,說明存在可行的行駛軌跡。
PRM算法相比基于搜索的算法,簡化了環(huán)境、提高了效率。但是在有狹窄通道場景中,很難采樣出可行路徑,效率會大幅降低。
RRT
快速探索隨機樹(Rapidly Exploring Random Trees,RRT),是Steven M. LaValle和James J. Kuffner Jr.在1998年提出的一種基于隨機生長樹思想實現(xiàn)對非凸高維空間快速搜索的算法。與PRM相同的是兩者都是基于隨機采樣的算法,不同的是PRM最終生成的是一個無向圖,而RRT生成的是一個隨機樹。RRT的最顯著特征就是具備空間探索的能力,即從一點向外探索拓展的特征。
RRT分單樹和雙樹兩種類型,單樹RRT將規(guī)起點作為隨機樹的根節(jié)點,通過隨機采樣、碰撞檢測的方式為隨機樹增加葉子節(jié)點,最終生成一顆隨機樹。而雙樹RRT則擁有兩顆隨機樹,分別以起點和終點為根節(jié)點,以同樣的方式進行向外的探索,直到兩顆隨機樹相遇,從而達到提高規(guī)劃效率的目的。
下面以圖28所示的地圖空間為例介紹單樹RRT算法的實現(xiàn)過程。在此地圖空間中,我們只知道起點A和終點B以及障礙物的位置(黑色的框)。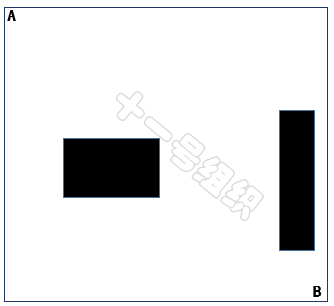
圖28 RRT算法舉例的地圖空間
對于單樹RRT算法,我們將起點A設置為隨機樹的根,并生成一個隨機采樣點,如圖27所示,隨機采樣點有下面這幾種情況。
(1)隨機采樣點1落在自由區(qū)域中,但是根節(jié)點A和隨機采樣點1之間的連線存在障礙物,無法通過碰撞檢測,采樣點1會被舍棄,重新再生成隨機采樣點。
(2)隨機采樣點2落在障礙物的位置,采樣點2也會被舍棄,重新再生成隨機采樣點。
(3)隨機采樣點3落在自由區(qū)域,且與根節(jié)點A之間的連線不存在障礙物,但是超過根節(jié)點的步長限制。但此時這個節(jié)點不會被簡單的舍棄點,而是會沿著根節(jié)點和隨機采樣點3的連線,找出符合步長限制的中間點,將這個中間點作為新的采樣點,也就是圖29中的4。
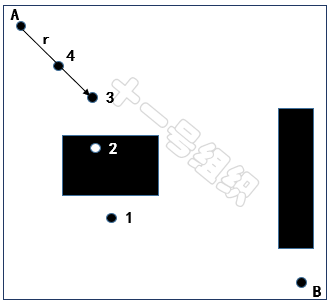
圖29 不同隨機采樣點舉例
接著我們繼續(xù)生成新的隨機采樣點,如果新的隨機采樣點位于自由區(qū)域,那么我們就可以遍歷隨機樹中已有的全部節(jié)點,找出距離新的隨機采樣點最近的節(jié)點,同時求出兩者之間的距離,如果滿足步長限制的話,我們將接著對這兩個節(jié)點進行碰撞檢測,如果不滿足步長限制的話,我們需要沿著新的隨機采樣點和最近的節(jié)點的連線方向,找出一個符合步長限制的中間點,用來替代新的隨機采樣點。最后如果新的隨機采樣點和最近的節(jié)點通過了碰撞檢測,就意味著二者之間存在邊,我們便可以將新的隨機采樣點添加進隨機樹中,并將最近的點設置為新的隨機采樣點的父節(jié)點。
重復上述過程,直到新的隨機采樣點在終點的步長限制范圍內(nèi),且滿足碰撞檢測。則將新的隨機采樣點設為終點B的父節(jié)點,并將終點加入隨機樹,從而完成迭代,生成如圖30所示的完整隨機樹。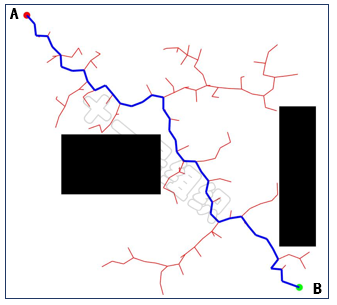
圖30隨機樹結(jié)算結(jié)果示例
相比PRM,RRT無需搜索步驟、效率更高。通過增量式擴展的方式,找到路徑后就立即結(jié)束,搜索終點的目的性更強。但是RRT作為一種純粹的隨機搜索算法,對環(huán)境類型不敏感,當?shù)貓D空間中存在狹窄通道時,因被采樣的概率低,導致算法的收斂速度慢,效率會大幅下降,有時候甚至難以在有狹窄通道的環(huán)境找到路徑。
圖31展示了 RRT應對存在狹窄通道地圖空間時的兩種表現(xiàn),一種是RRT很快就找到了出路,一種是一直被困在障礙物里面。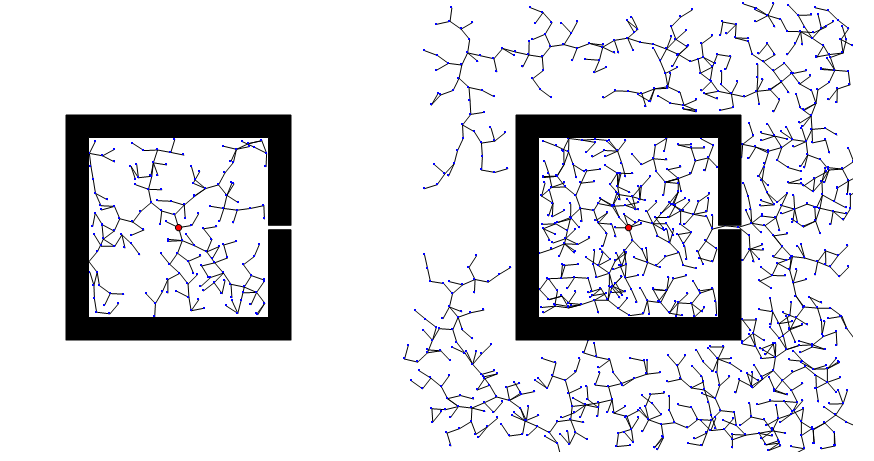
圖31 RRT面對狹窄通道時的表現(xiàn)
圍繞如何更好的“進行隨機采樣”、“定義最近的點”以及“進行樹的擴展”等方面,誕生了多種改進型的算法,包括雙樹RRT-Connect(雙樹)、lazy-RRT, RRT-Extend等。
PRM和RRT都是一個概率完備但非最優(yōu)的路徑規(guī)劃算法,也就是只要起點和終點之間存在有效的路徑,那么只要規(guī)劃的時間足夠長,采樣點足夠多,必然可以找到有效的路徑。但是這個解無法保證是最優(yōu)的。
采用PRM和RRT等隨機采樣算法生成的行駛軌跡,大多是一條條線段,線段之間的曲率也不不連續(xù),這樣的行駛軌跡是不能保證舒適性的,所以還需要進一步進行曲線平滑、角度平滑處理。代表算法是基于曲線插值的方法:RS曲線、Dubins曲線、多項式曲線、貝塞爾曲線和樣條曲線等。
所有基于曲線插值方法要解決的問題就是:在圖32上的若干點中,求出一條光滑曲線盡可能逼近所有點。下文以多項式曲線和貝塞爾曲線為例,介紹曲線插值算法的示例。
圖32 曲線插值方法要解決的問題描述
多項式曲線
找到一條曲線擬合所有的點,最容易想到的方法就是多項式曲線。常用的有三階多項式曲線、五階多項式曲線和七階多項式曲線。理論上只要多項式的階數(shù)足夠高,就可以擬合各種曲線。但從滿足需求和工程實現(xiàn)的角度,階數(shù)越低越好。
車輛在運動規(guī)劃中,舒適度是一個非常重要的指標,在物理中衡量舒適性的物理量為躍度(Jerk),它是加速度的導數(shù)。Jerk的絕對值越小意味著加速度的變化越平緩,加速度的變化越平緩意味著越舒適。而五次多項式曲線則被證明是在運動規(guī)劃中可以使Jerk比較小的多項式曲線。
以圖30所示換道場景為例,已知Frenet坐標系下?lián)Q道起點和終點的六個參數(shù)s0、v0、a0、st、vt、at,采用橫縱向解耦分別進行運動規(guī)劃的方法,可得橫向位置x(t)和縱向位置y(t)關于時間t的五次多項式表達式。
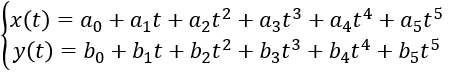
五次多項式中存在六個未知量,將起點和終點已知的六個參數(shù)代入便可這個六個未知量。然后根據(jù)時間t進行合并即可得到橫縱向聯(lián)合控制的曲線,即最終運動規(guī)劃的曲線。
貝塞爾曲線
對于比較少的點來說,采用多項式曲線非常合理。但是當點比較多時,為了逼近所有點,就不得不增加多項式的次數(shù),而由此帶來的負面影響就是曲線震蕩。退一步講,即使震蕩能夠被消除,獲得的曲線由于存在非常多的起伏,也不夠光順。而貝塞爾曲線的出現(xiàn),正好解決了上述問題。
1959年,法國數(shù)學家保爾·德·卡斯特里使用獨家配方求出貝塞爾曲線。1962年,法國雷諾汽車公司工程師皮埃爾·貝塞爾將自己在汽車造型設計的一些心得歸納總結(jié),并廣泛發(fā)表。貝塞爾在造型設計的心得可簡單總結(jié)為:先用折線段勾畫出汽車的外形大致輪廓,再用光滑的參數(shù)曲線去逼近這個折線多邊形。
繪制貝塞爾曲線之前,我們需要知道起點和終點的參數(shù),然后再提供任意數(shù)量的控制點的參數(shù)。如果控制點的數(shù)量為0,則為一階貝塞爾曲線,如果控制點的數(shù)量為1,則為二階貝塞爾曲線,如果控制點的數(shù)量為2,則為三階貝塞爾曲線,依次類推。不論是起點、終點還是控制點,它們均代表坐標系下的一個向量。
下面我們以經(jīng)典的二階貝塞爾曲線為例,介紹其繪制方法。如圖33所示,P0和P2為已知的參數(shù)的起點和終點,P1為已知參數(shù)的控制點。首先我們按照起點、控制點、終點的順序依次連接,生成兩條直線。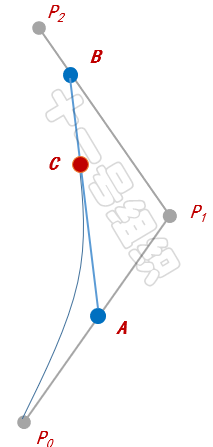
圖33 二階貝塞爾曲線示例
接著我們以每條直線的起點開始,向各自的終點按比例t取點,如圖中的A和B。隨后我們將A和B相連得到一條直線,也按相同的比例t取點,便可得到C點,這也是二階貝塞爾曲線在比例為t時會經(jīng)過的點。比列t滿足如下的公式。
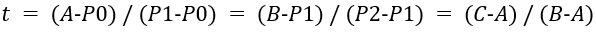
當我們比例t一點點變大(從0到1),就得到起點到終點的所有貝塞爾點,所有點相連便繪制出完整的二階貝塞爾曲線C(t),用公式表達為。
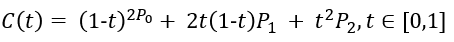
由二階貝塞爾曲線拓展到N階貝塞爾曲線,可得數(shù)學表達式如下。
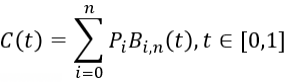
審核編輯:劉清
-
PRM
+關注
關注
0文章
14瀏覽量
4250 -
RRT
+關注
關注
0文章
12瀏覽量
1120 -
Dubins
+關注
關注
0文章
2瀏覽量
1937
原文標題:決策規(guī)劃系列:運動規(guī)劃常用算法
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
ZMC600E運動控制器T型、S型速度規(guī)劃詳解

外資制造業(yè)可利用AI提升決策能力
黑芝麻智能端到端算法參考模型公布
如何獲取到ZHCA660應用文檔內(nèi)RF DAC的頻率規(guī)劃計算工具?
多臺倉儲AGV協(xié)作全局路徑規(guī)劃算法的研究

激光雷達在城市規(guī)劃中的應用
淺談基于儲能電站提高風電消納能力的電源規(guī)劃研究
智慧產(chǎn)業(yè)園區(qū)規(guī)劃的注意事項
【Vision Board創(chuàng)客營連載體驗】基于RA8D1-Vision Board的自動路徑規(guī)劃小車
英偉達GPU新品規(guī)劃與HBM市場展望
運動控制算法有哪些
谷歌Gemini新增旅行規(guī)劃功能,助用戶高效規(guī)劃度假行程
VADv2:基于概率性規(guī)劃的端到端自動駕駛
沖壓自動線規(guī)劃的幾點考慮





 決策規(guī)劃系列:運動規(guī)劃常用算法
決策規(guī)劃系列:運動規(guī)劃常用算法










評論