來源:DeepHub IMBA
如果你剛剛開始學習神經網絡,激活函數的原理一開始可能很難理解。但是如果你想開發強大的神經網絡,理解它們是很重要的。
神經網絡架構
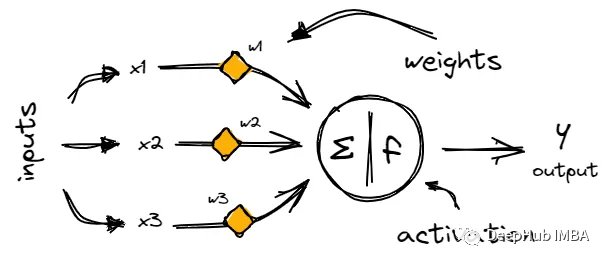
神經網絡由稱為神經元的鏈接節點層組成,神經元通過稱為突觸的加權連接來處理和傳輸信息。
每個神經元從上一層的神經元獲取輸入,對其輸入的和應用激活函數,然后將輸出傳遞給下一層。
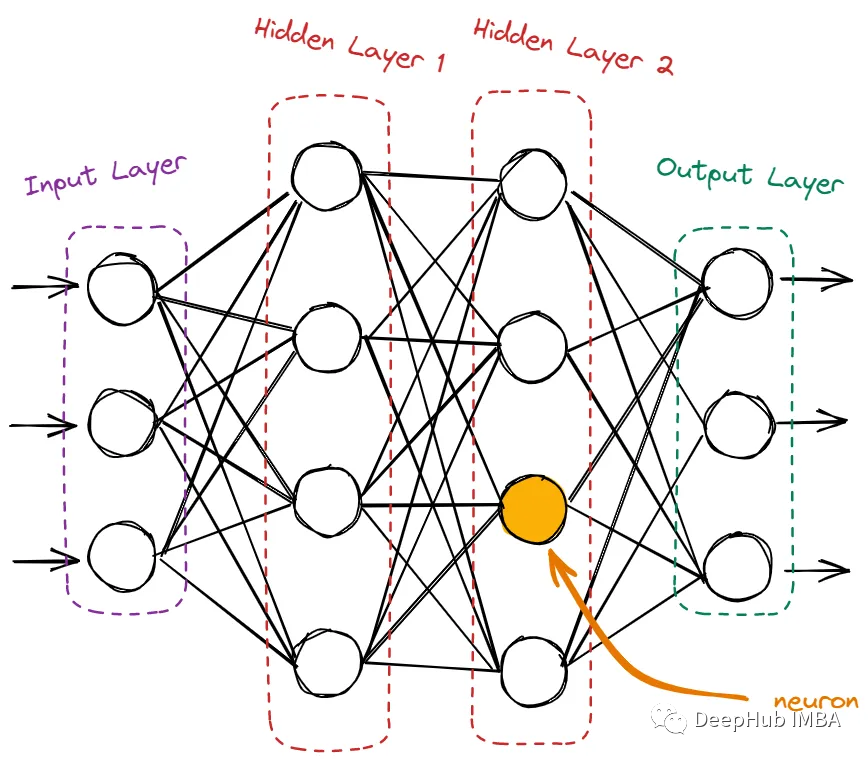
神經網絡的神經元包含輸入層、隱藏層和輸出層。
輸入層只接收來自域的原始數據。這里沒有計算,節點只是簡單地將信息(也稱為特征)傳遞給下一層,即隱藏層。隱藏層是所有計算發生的地方。它從輸入層獲取特征,并在將結果傳遞給輸出層之前對它們進行各種計算。輸出層是網絡的最后一層。它使用從隱藏層獲得的所有信息并產生最終值。
為什么需要激活函數。為什么神經元不能直接計算并將結果轉移到下一個神經元?激活函數的意義是什么?激活函數在神經網絡中的作用
網絡中的每個神經元接收來自其他神經元的輸入,然后它對輸入進行一些數學運算以生成輸出。一個神經元的輸出可以被用作網絡中其他神經元的輸入。
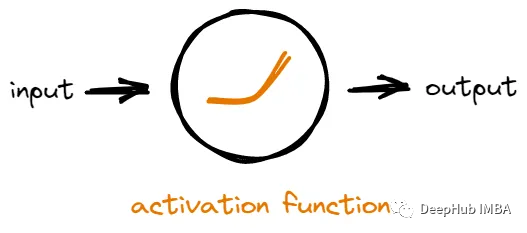
如果沒有激活函數,神經元將只是對輸入進行線性數學運算。這意味著無論我們在網絡中添加多少層神經元,它所能學習的東西仍然是有限的,因為輸出總是輸入的簡單線性組合。
激活函數通過在網絡中引入非線性來解決問題。通過添加非線性,網絡可以模擬輸入和輸出之間更復雜的關系,從而發現更多有價值的模式。
簡而言之,激活函數通過引入非線性并允許神經網絡學習復雜的模式,使神經網絡更加強大。理解不同類型的激活函數
我們可以將這些函數分為三部分:二元、線性和非線性。
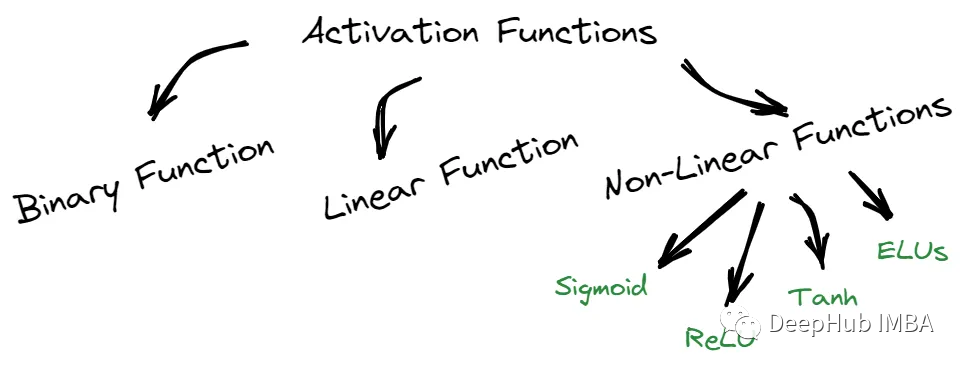
二元函數只能輸出兩個可能值中的一個,而線性函數則返回基于線性方程的值。
非線性函數,如sigmoid函數,Tanh, ReLU和elu,提供的結果與輸入不成比例。每種類型的激活函數都有其獨特的特征,可以在不同的場景中使用。1、Sigmoid / Logistic激活函數
Sigmoid激活函數接受任何數字作為輸入,并給出0到1之間的輸出。輸入越正,輸出越接近1。另一方面,輸入越負,輸出就越接近0,如下圖所示。
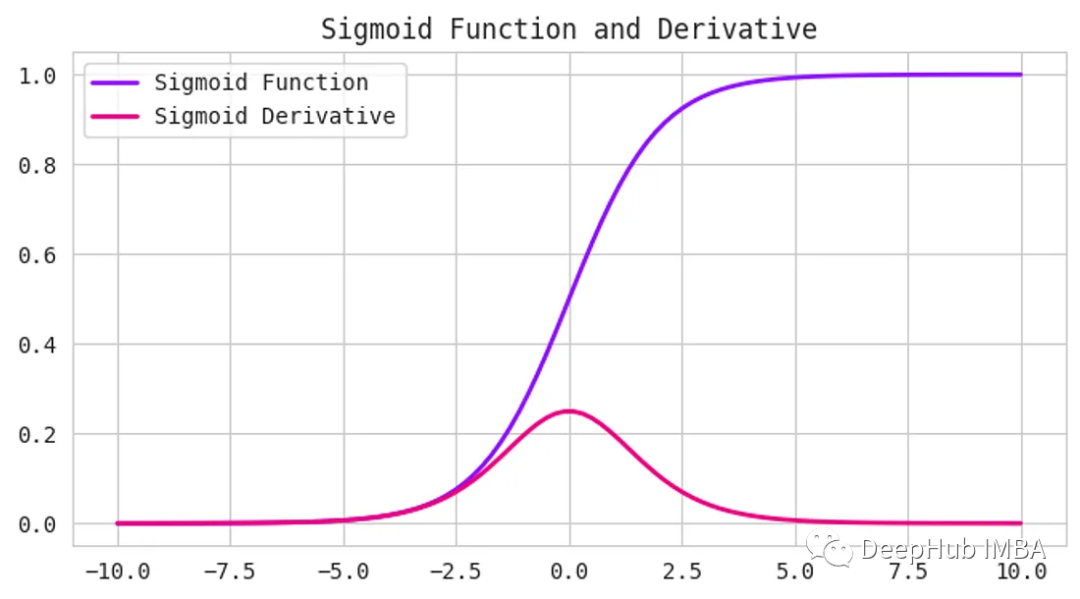
它具有s形曲線,使其成為二元分類問題的理想選擇。如果要創建一個模型來預測一封電子郵件是否為垃圾郵件,我們可以使用Sigmoid函數來提供一個0到1之間的概率分數。如果得分超過0.5分,則認為該郵件是垃圾郵件。如果它小于0.5,那么我們可以說它不是垃圾郵件。
函數定義如下:

但是Sigmoid函數有一個缺點——它受到梯度消失問題的困擾。當輸入變得越來越大或越來越小時,函數的梯度變得非常小,減慢了深度神經網絡的學習過程,可以看上面圖中的導數(Derivative)曲線。
但是Sigmoid函數仍然在某些類型的神經網絡中使用,例如用于二進制分類問題的神經網絡,或者用于多類分類問題的輸出層,因為預測每個類的概率Sigmoid還是最好的解決辦法。2、Tanh函數(雙曲正切)
Tanh函數,也被稱為雙曲正切函數,是神經網絡中使用的另一種激活函數。它接受任何實數作為輸入,并輸出一個介于-1到1之間的值。
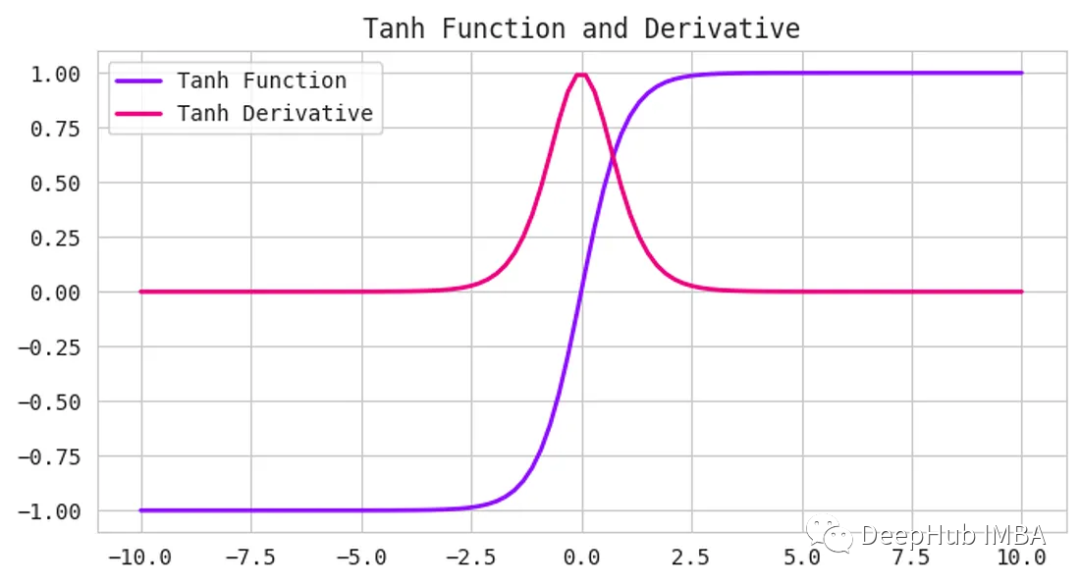
Tanh函數和Sigmoid函數很相似,但它更以0為中心。當輸入接近于零時,輸出也將接近于零。這在處理同時具有負值和正值的數據時非常有用,因為它可以幫助網絡更好地學習。
函數定義如下:
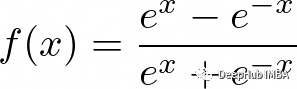
3、線性整流單元/ ReLU函數
ReLU是一種常見的激活函數,它既簡單又強大。它接受任何輸入值,如果為正則返回,如果為負則返回0。換句話說,ReLU將所有負值設置為0,并保留所有正值。
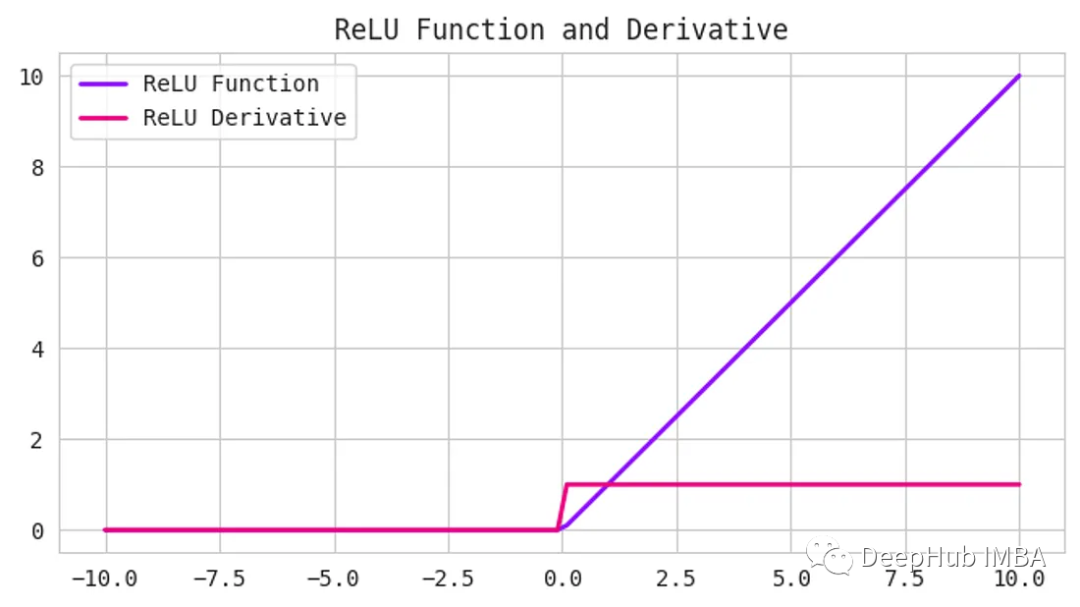
函數定義如下:
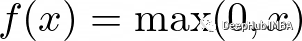
使用ReLU的好處之一是計算效率高,并且實現簡單。它可以幫助緩解深度神經網絡中可能出現的梯度消失問題。
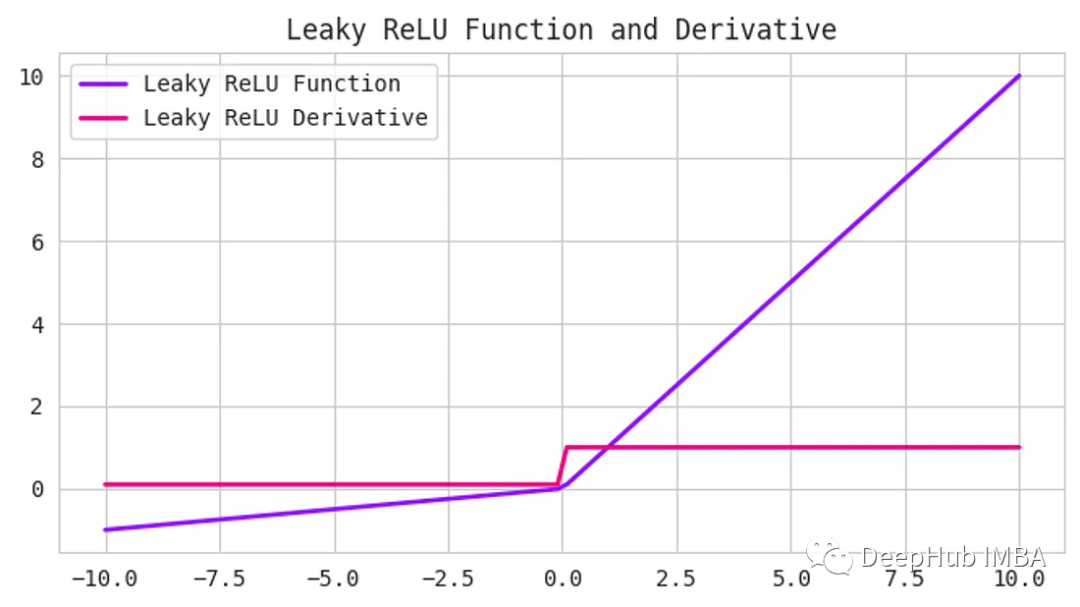
但是,ReLU可能會遇到一個被稱為“dying ReLU”問題。當神經元的輸入為負,導致神經元的輸出為0時,就會發生這種情況。如果這種情況發生得太頻繁,神經元就會“死亡”并停止學習。4、Leaky ReLU
Leaky ReLU函數是ReLU函數的一個擴展,它試圖解決“dying ReLU”問題。Leaky ReLU不是將所有的負值都設置為0,而是將它們設置為一個小的正值,比如輸入值的0.1倍。他保證即使神經元接收到負信息,它仍然可以從中學習。
函數定義如下:
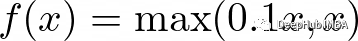
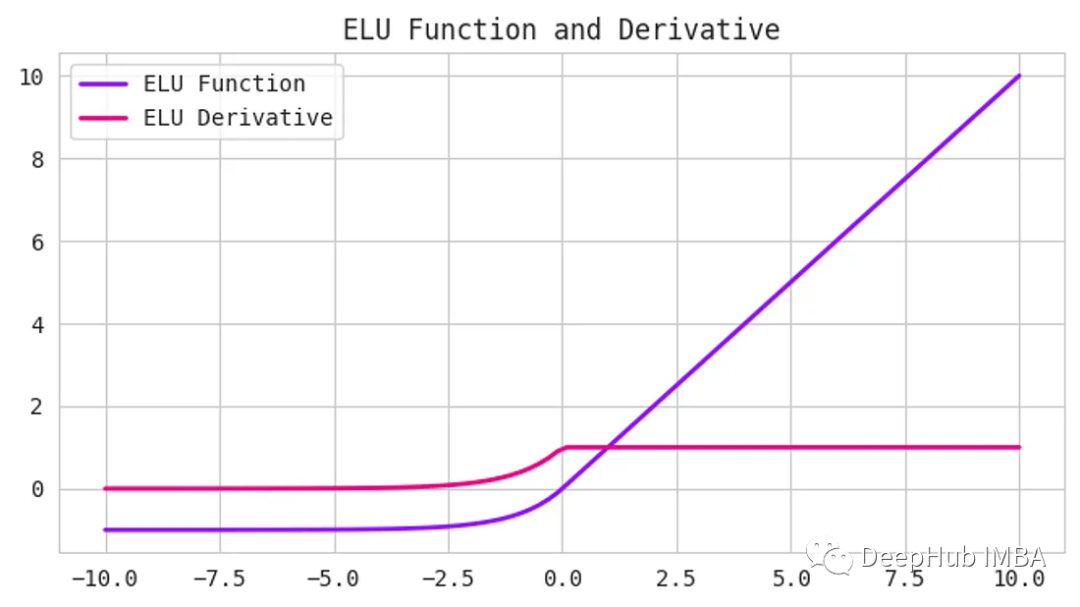
5、指數線性單位(elu)函數
ReLU一樣,他們的目標是解決梯度消失的問題。elu引入了負輸入的非零斜率,這有助于防止“dying ReLU”問題
公式為:
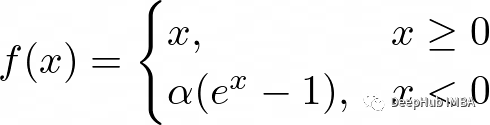
這里的alpha是控制負飽和度的超參數。
與ReLU和tanh等其他激活函數相比,elu已被證明可以提高訓練和測試的準確性。它在需要高準確度的深度神經網絡中特別有用。6、Softmax函數
在需要對輸入進行多類別分類的神經網絡中,softmax函數通常用作輸出層的激活函數。它以一個實數向量作為輸入,并返回一個表示每個類別可能性的概率分布。
softmax的公式是:
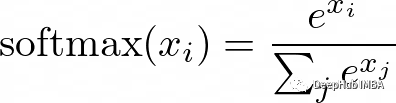
這里的x是輸入向量,i和j是從1到類別數的索引。
Softmax對于多類分類問題非常有用,因為它確保輸出概率之和為1,從而便于解釋結果。它也是可微的,這使得它可以在訓練過程中用于反向傳播。7、Swish
Swish函數是一個相對較新的激活函數,由于其優于ReLU等其他激活函數的性能,在深度學習社區中受到了關注。
Swish的公式是:
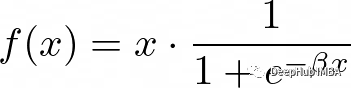
這里的beta是控制飽和度的超參數。
Swish類似于ReLU,因為它是一個可以有效計算的簡單函數。并且有一個平滑的曲線,有助于預防“dying ReLU”問題。Swish已被證明在各種深度學習任務上優于ReLU。
選擇哪一種?
首先,需要將激活函數與你要解決的預測問題類型相匹配。可以從ReLU激活函數開始,如果沒有達到預期的結果,則可以轉向其他激活函數。
以下是一些需要原則:- ReLU激活函數只能在隱藏層中使用。
- Sigmoid/Logistic和Tanh函數不應該用于隱藏層,因為它們會在訓練過程中引起問題。
-
Swish函數用于深度大于40層的神經網絡會好很多。
-
回歸-線性激活函數
-
二元分類- Sigmoid
-
多類分類- Softmax
- 多標簽分類- Sigmoid
END
推薦閱讀 對話Imagination中國區董事長:以GPU為支點加強軟硬件協同,助力數字化轉型合作案例 | Imagination車規級硬件虛擬化幫助Telechips提升顯示器的多樣性
Imagination Technologies是一家總部位于英國的公司,致力于研發芯片和軟件知識產權(IP),基于Imagination IP的產品已在全球數十億人的電話、汽車、家庭和工作 場所中使用。獲取更多物聯網、智能穿戴、通信、汽車電子、圖形圖像開發等前沿技術信息,歡迎關注 Imagination Tech!
原文標題:神經網絡初學者的激活函數指南
文章出處:【微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
-
imagination
+關注
關注
1文章
573瀏覽量
61349
原文標題:神經網絡初學者的激活函數指南
文章出處:【微信號:Imgtec,微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 神經網絡初學者的激活函數指南
神經網絡初學者的激活函數指南










評論