解決一個回溯問題,實際上就是一個決策樹的遍歷過程 。你只需要思考 3 個問題:
1、 路徑 :也就是已經(jīng)做出的選擇。
2、選擇列表 :也就是你當前可以做的選擇。
3、結束條件 :也就是到達決策樹底層,無法再做選擇的條件。
如果你不理解這三個詞語的解釋,沒關系,我們后面會用「全排列」和「N 皇后問題」這兩個經(jīng)典的回溯算法問題來幫你理解這些詞語是什么意思,現(xiàn)在你先留著印象。
代碼方面,回溯算法的框架:
result = []
def backtrack(路徑, 選擇列表):
if 滿足結束條件:
result.add(路徑)
return
for 選擇 in 選擇列表:
做選擇
backtrack(路徑, 選擇列表)
撤銷選擇
其核心就是 for 循環(huán)里面的遞歸,在遞歸調用之前「做選擇」,在遞歸調用之后「撤銷選擇」 ,特別簡單。
什么叫做選擇和撤銷選擇呢,這個框架的底層原理是什么呢?下面我們就通過「全排列」這個問題來解開之前的疑惑,詳細探究一下其中的奧妙!
一、全排列問題
我們在高中的時候就做過排列組合的數(shù)學題,我們也知道n個不重復的數(shù),全排列共有 n! 個。
PS: 為了簡單清晰起見,我們這次討論的全排列問題不包含重復的數(shù)字 。
那么我們當時是怎么窮舉全排列的呢?比方說給三個數(shù)[1,2,3],你肯定不會無規(guī)律地亂窮舉,一般是這樣:
先固定第一位為 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位變成 3,第三位就只能是 2 了;然后就只能變化第一位,變成 2,然后再窮舉后兩位……
其實這就是回溯算法,我們高中無師自通就會用,或者有的同學直接畫出如下這棵回溯樹:
只要從根遍歷這棵樹,記錄路徑上的數(shù)字,其實就是所有的全排列。 我們不妨把這棵樹稱為回溯算法的「決策樹」 。
為啥說這是決策樹呢,因為你在每個節(jié)點上其實都在做決策 。比如說你站在下圖的紅色節(jié)點上:
你現(xiàn)在就在做決策,可以選擇 1 那條樹枝,也可以選擇 3 那條樹枝。為啥只能在 1 和 3 之中選擇呢?因為 2 這個樹枝在你身后,這個選擇你之前做過了,而全排列是不允許重復使用數(shù)字的。
現(xiàn)在可以解答開頭的幾個名詞:[2]就是「路徑」,記錄你已經(jīng)做過的選擇;[1,3]就是「選擇列表」,表示你當前可以做出的選擇;「結束條件」就是遍歷到樹的底層,在這里就是選擇列表為空的時候 。
如果明白了這幾個名詞,可以把「路徑」和「選擇 列表 」作為決策樹上每個節(jié)點的屬性 ,比如下圖列出了幾個節(jié)點的屬性:
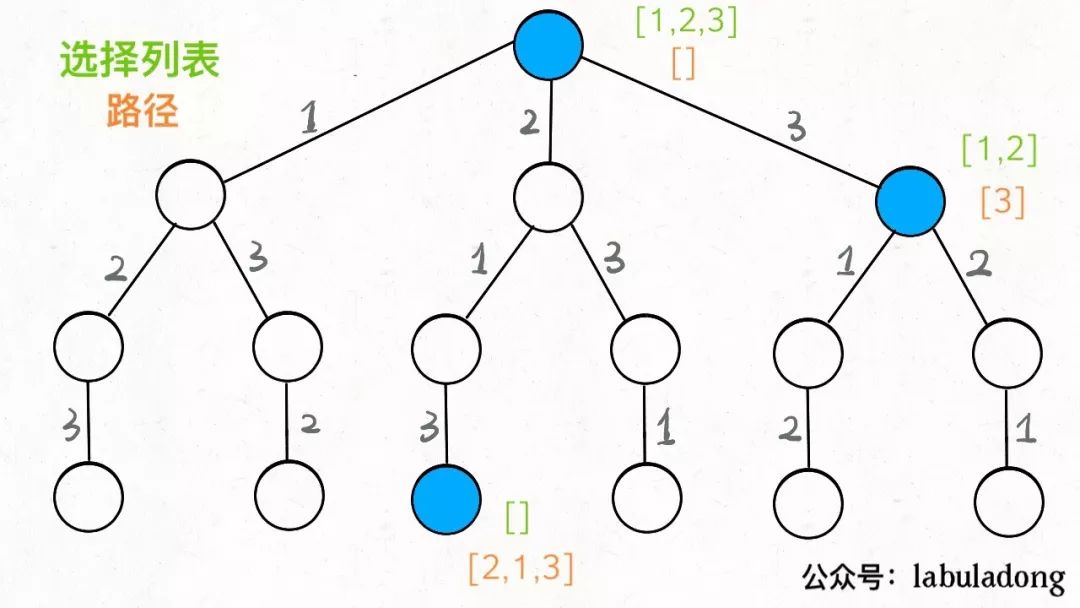
我們定義的backtrack函數(shù)其實就像一個指針,在這棵樹上游走,同時要正確維護每個節(jié)點的屬性,每當走到樹的底層,其「路徑」就是一個全排列 。
再進一步,如何遍歷一棵樹?這個應該不難吧。回憶一下之前 [學習數(shù)據(jù)結構的框架思維]寫過,各種搜索問題其實都是樹的遍歷問題,而多叉樹的遍歷框架就是這樣:
void traverse(TreeNode root) {
for (TreeNode child : root.childern)
// 前序遍歷需要的操作
traverse(child);
// 后序遍歷需要的操作
}
而所謂的前序遍歷和后序遍歷,他們只是兩個很有用的時間點,我給你畫張圖你就明白了:

前序遍歷的代碼在進入某一個節(jié)點之前的那個時間點執(zhí)行,后序遍歷代碼在離開某個節(jié)點之后的那個時間點執(zhí)行 。
回想我們剛才說的,「路徑」和「選擇」是每個節(jié)點的屬性,函數(shù)在樹上游走要正確維護節(jié)點的屬性,那么就要在這兩個特殊時間點搞點動作:

現(xiàn)在,你是否理解了回溯算法的這段核心框架?
for 選擇 in 選擇列表:
# 做選擇
將該選擇從選擇列表移除
路徑.add(選擇)
backtrack(路徑, 選擇列表)
# 撤銷選擇
路徑.remove(選擇)
將該選擇再加入選擇列表
我們只要在遞歸之前做出選擇,在遞歸之后撤銷剛才的選擇 ,就能正確得到每個節(jié)點的選擇列表和路徑。
下面,直接看全排列代碼:
List<List<Integer>> res = new LinkedList<>();
/* 主函數(shù),輸入一組不重復的數(shù)字,返回它們的全排列 */
List<List<Integer>> permute(int[] nums) {
// 記錄「路徑」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
// 路徑:記錄在 track 中
// 選擇列表:nums 中不存在于 track 的那些元素
// 結束條件:nums 中的元素全都在 track 中出現(xiàn)
void backtrack(int[] nums, LinkedList<Integer> track) {
// 觸發(fā)結束條件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的選擇
if (track.contains(nums[i]))
continue;
// 做選擇
track.add(nums[i]);
// 進入下一層決策樹
backtrack(nums, track);
// 取消選擇
track.removeLast();
}
}
我們這里稍微做了些變通,沒有顯式記錄「選擇列表」,而是通過nums和track推導出當前的選擇列表
至此,我們就通過全排列問題詳解了回溯算法的底層原理。當然,這個算法解決全排列不是很高效,因為對鏈表使用contains方法需要 O(N) 的時間復雜度。有更好的方法通過交換元素達到目的,但是難理解一些,這里就不寫了,有興趣可以自行搜索一下。
但是必須說明的是,不管怎么優(yōu)化,都符合回溯框架,而且時間復雜度都不可能低于 O(N!),因為窮舉整棵決策樹是無法避免的。 這也是回溯算法的一個特點,不像動態(tài)規(guī)劃存在重疊子問題可以優(yōu)化,回溯算法就是純暴力窮舉,復雜度一般都很高 。
明白了全排列問題,就可以直接套回溯算法框架了,下面簡單看看 N 皇后問題。
二、N 皇后問題
這個問題很經(jīng)典了,簡單解釋一下:給你一個 N×N 的棋盤,讓你放置 N 個皇后,使得它們不能互相攻擊。
PS:皇后可以攻擊同一行、同一列、左上左下右上右下四個方向的任意單位。
這是 N = 8 的一種放置方法:

圖片來自 LeetCode
這個問題本質上跟全排列問題差不多,決策樹的每一層表示棋盤上的每一行;每個節(jié)點可以做出的選擇是,在該行的任意一列放置一個皇后。
直接套用框架:
vector
這部分主要代碼,跟全排列問題差不多。isValid函數(shù)的實現(xiàn)也很簡單:
/* 是否可以在 board[row][col] 放置皇后? */
bool isValid(vector {
int n = board.size();
// 檢查列是否有皇后互相沖突
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q')
return false;
}
// 檢查右上方是否有皇后互相沖突
for (int i = row - 1, j = col + 1;
i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q')
return false;
}
// 檢查左上方是否有皇后互相沖突
for (int i = row - 1, j = col - 1;
i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q')
return false;
}
return true;
}
函數(shù)backtrack依然像個在決策樹上游走的指針,每個節(jié)點就表示在board[row][col]上放置皇后,通過isValid函數(shù)可以將不符合條件的情況剪枝
如果直接給你這么一大段解法代碼,可能是懵逼的。但是現(xiàn)在明白了回溯算法的框架套路,還有啥難理解的呢?無非是改改做選擇的方式,排除不合法選擇的方式而已,只要框架存于心,你面對的只剩下小問題了。
當N = 8時,就是八皇后問題,數(shù)學大佬高斯窮盡一生都沒有數(shù)清楚八皇后問題到底有幾種可能的放置方法,但是我們的算法只需要一秒就可以算出來所有可能的結果。
不過真的不怪高斯。這個問題的復雜度確實非常高,看看我們的決策樹,雖然有isValid函數(shù)剪枝,但是最壞時間復雜度仍然是 O(N^(N+1)),而且無法優(yōu)化。如果N = 10的時候,計算就已經(jīng)很耗時了。
有的時候,我們并不想得到所有合法的答案,只想要一個答案,怎么辦呢 ?比如解數(shù)獨的算法,找所有解法復雜度太高,只要找到一種解法就可以。
其實特別簡單,只要稍微修改一下回溯算法的代碼即可:
// 函數(shù)找到一個答案后就返回 true
bool backtrack(vector {
// 觸發(fā)結束條件
if (row == board.size()) {
res.push_back(board);
return true;
}
...
for (int col = 0; col < n; col++) {
...
board[row][col] = 'Q';
if (backtrack(board, row + 1))
return true;
board[row][col] = '.';
}
return false;
}
這樣修改后,只要找到一個答案,for 循環(huán)的后續(xù)遞歸窮舉都會被阻斷。也許你可以在 N 皇后問題的代碼框架上,稍加修改,寫一個解數(shù)獨的算法?
三、最后總結
回溯算法就是個多叉樹的遍歷問題,關鍵就是在前序遍歷和后序遍歷的位置做一些操作,算法框架如下:
def backtrack(...):
for 選擇 in 選擇列表:
做選擇
backtrack(...)
撤銷選擇
寫backtrack函數(shù)時,需要維護走過的「路徑」和當前可以做的「選擇列表」,當觸發(fā)「結束條件」時,將「路徑」記入結果集 。
其實想想看,回溯算法和動態(tài)規(guī)劃是不是有點像呢?我們在動態(tài)規(guī)劃系列文章中多次強調,動態(tài)規(guī)劃的三個需要明確的點就是「狀態(tài)」「選擇」和「base case」,是不是就對應著走過的「路徑」,當前的「選擇列表」和「結束條件」?
某種程度上說,動態(tài)規(guī)劃的暴力求解階段就是回溯算法。只是有的問題具有重疊子問題性質,可以用 dp table 或者備忘錄優(yōu)化,將遞歸樹大幅剪枝,這就變成了動態(tài)規(guī)劃。而今天的兩個問題,都沒有重疊子問題,也就是回溯算法問題了,復雜度非常高是不可避免的。
-
回溯算法
+關注
關注
0文章
10瀏覽量
6623 -
for循環(huán)
+關注
關注
0文章
61瀏覽量
2530
發(fā)布評論請先 登錄
相關推薦
回溯經(jīng)典 (五皇后問題) (算法)
算法設計與分析王曉東

一種無回溯的最長前綴匹配搜索算法
基于回溯的RFID防沖撞算法
模板方法模式在回溯算法中的應用
模板方法模式在回溯算法中的應用
求組合問題的不同算法比較分析
Viterbi譯碼器回溯算法實現(xiàn)

基于回溯搜索優(yōu)化算法改進矩陣填充的指紋庫構建
回溯的共軛梯度迭代硬閾值算法如何解決迭代次數(shù)多重構時間長的問題
C語言重解經(jīng)典回溯算法案例

關于回溯算法的介紹與運用
算法時空復雜度分析實用指南(上)
算法時空復雜度分析實用指南(下)





 回溯算法技巧分析
回溯算法技巧分析











評論