我們重點就講一個事情:
怎么讓三相繞組變成我們心里想要的那個電磁鐵!
也就是能給出360°任意指向的一個磁場矢量,同時這個磁場矢量的大小我們也能任意控制!
我們先看簡單的定子,假設就是三個齒一對極的,因為任何多個齒的都是可以看成是n個3齒的組合,圖中有ABC三個繞組,上一節我們說過,兩個正交的繞組分別給電可以形成xy坐標下的任意一個方向的矢量,現在這里有三個繞組了怎么實現?
三個繞組分別給電當然是可以的,這是最簡單的,因為兩個繞組都可以做到,更何況三個繞組呢,但是現實是三個繞組分別給電,我們需要接6個線頭,A+和A-,B+和B-,C+和C-,每個繞組的磁力和大小(正反)要控制,都要一個h橋,這樣我們就要3個h橋了,這顯然是很大的浪費!
H橋控制線圈如下:
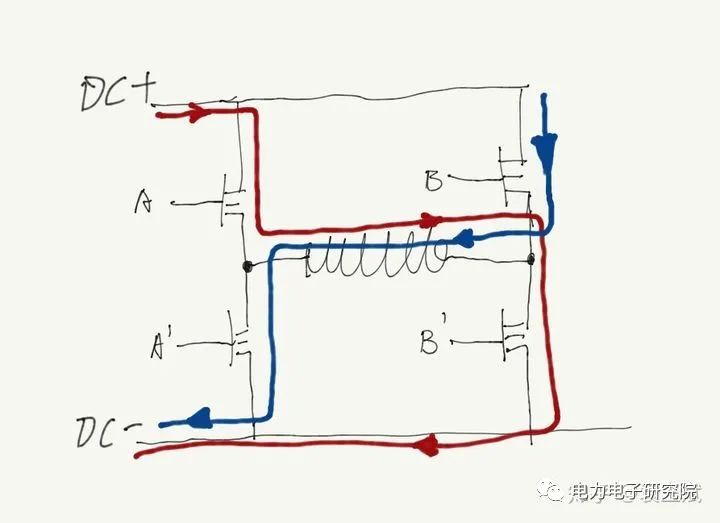
圖2
圖中,是一個線圈在中間,有4個mos,A和B’打開的時候,線圈電流則是紅色箭頭方向,B和A‘打開的時候,線圈電流則是藍色方向,通電羅線圈電流方向和磁力方向就很明顯了;紅色方向電流產生電時候,改變A和B'同時導通電時間,其它時間mos是全部關閉的,這樣能調整DC電壓加載在線圈上電有效時間,這就等效成一個小電壓加在線圈上了,比如一半電時間A和B'打開,一半電時間所有電mos都關閉,則相當于0.5VDC加在線圈上了,如果全部時間A和B’都是打開的,則相當于VDC加在線圈上了,之所以電壓能這樣等效的原因是因為線圈是電感,實際線圈上感受到的電壓是在VDC和0之間變化的,但是電流是連續的,電流連續,線圈產生的磁場也就是連續的(實際電流也是上升下降的,但是電壓變動很快的話,電感夠大,理論可以做到電流連續,如下圖)
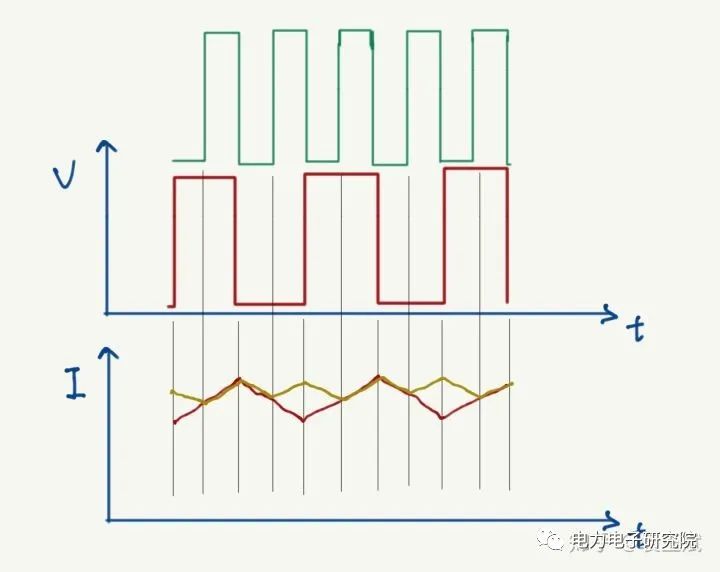
圖3
如圖電壓都是50占空比,綠線和紅線,對應的電流就如下圖中的黃色和紅色,占空比一樣的情況下,頻率越高,電流波動的峰峰值就越小了(具體電流的高度不深糾,主要示意一下)!
回到上面的ABC三相電圖,如果我們分別控制三個線圈,我們要3個H橋,但是前人要聰明的多,假如我們把圖1的A-,B-,C-全部連接在一起,然后只控制A+,B+,C+怎么樣,這樣我們做一下假設,A給高電平,A'給低電平,讓這個控制的上邊mos打開,下邊mos關閉,則有了A+連接DC+;B給低電平,B’給高電平,讓這邊控制的上臂mos關閉,下臂mos打開,則B+連接了DC-,同理和B一樣的操作,讓C+連接DC-;------------------方法一

圖4
保持上面的這樣的接法,這樣我們能發現,電流從A進入,B,C流出,如圖5的1所示的,
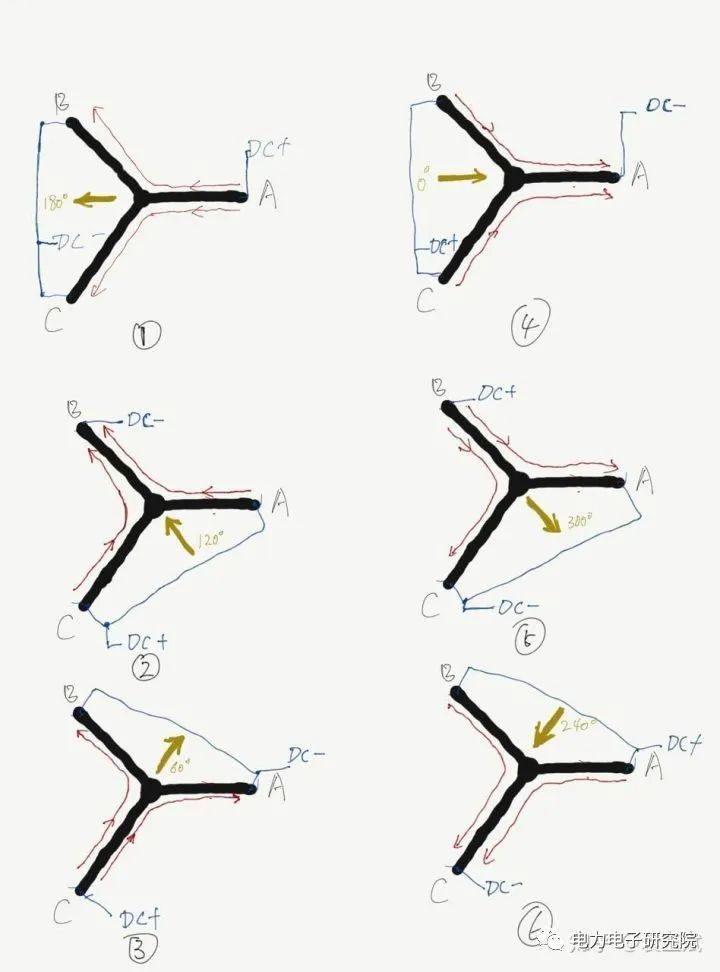
圖5
這樣橘黃色的箭頭方向和電磁鐵形成的磁場方向一致,
但是這里我們把橘黃色箭頭稱呼為電壓矢量的方向,因為這里我們加載的是電壓方向,A指向B和C,由于是穩態的,所以電流方向也是這個方向,所以磁場方向和橘色箭頭一致了,
要是這個橘色電壓方向旋轉起來后,一般來看,磁場的方向是滯后與這個箭頭方向的(不是90°),
因為定子里面是電感-電阻模型,我們知道純電感中,電流滯后電壓90°相位,這里因為有電阻,實際上還有轉子永磁反電動勢,所以滯后的角度和你的電流大小,頻率都有關系,但是我們知道是滯后的就好了;
知道上面的關系,我們這里嚴謹一點,這一章節我們說這個控制不是控制電磁鐵產生360°任意指向的磁場,而是把電磁鐵上加載的電壓矢量控制到360°的任意指向,同時控制這個電壓矢量的幅值,
電壓矢量的方向任意控制了,大小任意可以控制了,相信電流矢量的方向和大小當然也是可以任意控制了,我們先研究電壓矢量方向大小任意控制;
這樣我們回到圖5,重復圖5中1的操作,我們可以復制出來2,3,4,5,6的操作,這些操作就是重復圖4中的 方法一, 但是改變了mos管子接通的上下關系,這樣我們就得到了6個狀態了,圖5中我標注出來了,大家仔細看會發現這6個狀態的方向依次是差60°的方向,如果我們把通電的順序按照,4,3,2,1,6,5,4這樣動起來,你看看是不是出現了旋轉的電壓矢量了!

圖6
沒錯啊,這就是我們的6個旋轉電壓矢量,這也是有感的方波里面,人家常用的伎倆,
簡單的描述,就是連續的給這樣的6個方向的接通時序,假如他檢測到電機的轉子d軸(電控入門一中解釋了d軸)在0度的位置,它就給120°這個電壓矢量,轉子d軸到了60°,它就給180°的這個電壓矢量,如此一步一步的來控制電機旋轉,也就是我們大家常常說的6步換向,
六步換向也是可以控制這個電壓矢量的幅值的,它控制幅值的方式是圖4的方法一中,控制B,C連接的下臂mos一直導通,但是A連接的上臂mos不斷的 開關 ,當A連接的上臂mos關閉的時候,A和DC+斷開了,DC+-電壓加不到ABC上,是高阻態,只有A連接的上臂mos導通的時候,DC+-,才能加載在ABC上,這樣控制開關的占空比,則能夠控制的了電壓矢量的作用時間,微觀來看,就是有-無-有-無-有這樣夾在一起,控制這個有無的時間比重就控制了電壓矢量的等效幅值了, 簡單的說就是在插入了斷路時許到通路時序中 ;(實際斷路時序中,看圖4,A相的上臂mos管,下臂mos管都關了,但是A相里面還有電流,電流從哪進入A相的呢,電流是從A相連接的半橋的下臂mos管的體二極管里由下向上流動的,也就是俗稱的續流)-----------------------方法二
多說一句,這里說等效的電壓矢量幅值,為什么是等效,因為電感模型中,電壓是可以突變的,但是電流是不能突變的,如果你拿示波器去夾在A和星接點上,看A相的分壓,你會發現,這個分壓就是有無有無的節奏,但是如果你拿電流鉗鉗在A相上看電流,你會發現這個電流是一直在的,只是有點波動,三角鋸齒波的形狀的波動,開關的頻率越高,電流波形頻率也越高,波動幅度越低,也越接近直流,電流是連續的,所以電壓我們這里說等效,這也是伏秒原則的緣由;
而這里我們要用的是svpwm,會更加有趣,有趣在哪里?
1.svpwm就是我們要脫開這有限的6個方向,我們要制造無限個連續的方向填充滿360°,
2.svpwm的調整電壓矢量的等效幅值,是通過插入主動短路的零矢量作用時間來完成,而不是 斷路 ;
主動短路的零矢量就是方法二中的A相的上臂mos關閉,下臂mos也關閉,變成A相的下臂mos打開;B,C相的下臂mos也打開,想想會有什么問題嗎?肯定沒有問題啊,原來方法二中,你想把A相的上臂mos關閉,A相的下臂mos本來就是關閉的,但是奈何這個下臂mos不爭氣,身體里面有個反骨(圖4),這個二極管,它就給你把電導通了,那如其這樣,還不如我主動給你下臂的mos給打開呢,對不對!這個一打開就是A,B,C的下臂mos都是開了上臂mos全關閉,這就是我們說的零矢量,
那愛思考的同學想說,為啥不有A,B,C的上臂mos都打開,下臂mos都關閉行不行?
聰明,當然可以的,你已經抓到了另外一個零矢量了,
這樣2個零矢量,結合6個不同方向的電壓矢量,一共你找到了8個可控的通電時序了,這8個通電時序,有機的組合在一起,將能構成奇妙的svpwm;
我們提到了8種通電時序,我們做個規定,每一相的半橋,什么是半橋?圖4的A和A'這兩個所在的mos構成的叫做A相半橋,上臂的mos打開下臂的mos關閉,我們記作1,上臂的mos關閉,下臂的mos打開我們記作0;
有沒有上下臂的mos同時打開的情況?沒有,這樣會短路;
有沒有上下臂mos同時關閉的情況?svpwm中除了上臂mos管關閉,下臂mos管還沒打開,或者下臂mos管關閉,上臂mos管還沒打開的死區內,其他情況下沒有,而六步方波中是存在的!
我們把上臂mos管簡單的稱呼一下叫做上管,下臂的mos管叫做下管,有A,B,C三相,每一相有兩種可能,一起排列組合有2^3種可能,這樣上下管的8種搭配就是:
方便閱讀,我把圖6再搬到這里

圖6
(0,0,0) A下管打開,B下管打開,C下管打開,對應圖6中的中心點
(0,0,1) A下管打開,B下管打開,C上管打開,對應圖6中的60°
(0,1,0) A下管打開,B上管打開,C下管打開,對應圖6中的300°
(0,1,1) A下管打開,B上管打開,C上管打開,對應圖6中的0°
(1,0,0) A上管打開,B下管打開,C下管打開,對應圖6中的180°
(1,0,1) A上管打開,B下管打開,C上管打開,對應圖6中的120°
(1,1,0) A上管打開,B上管打開,C下管打開,對應圖6中的240°
(1,1,1) A上管打開,B上管打開,C上管打開,對應圖6中的中心點
以上說到的上管打開,默認的下管就是關閉,下管打開,默認的上管就是關閉;
以上的每個組合看作一個矢量,于是有了這8個基礎矢量,8個基礎矢量怎么構成平面內任意方向的矢量?比如我們想讓電壓矢量指向24°,怎么辦?--------------------問題1



SVPWM的基本思想也是這樣,
1.用6個非零的矢量的相鄰的兩個矢量來控制合成矢量的方向,
2.用零矢量來調整合成矢量的幅值
回到問題1,產生24°方向的矢量,我們要使用圖6中的0°和60°兩個非零基礎矢量來合成,然后24°方向的矢量的幅值我們用零矢量的摻入來調整;
非零基礎矢量的模長是多長?
我這里用矢量變換的原則,比如說基礎的非零矢量(0,1,1)的模長表示多大?
矢量合成,看圖5的第4個,方便閱讀,我這里再插入一次

圖5





圖8(網扒,侵刪)
上面我們提到的ARR和CCR是stm32中的概念,這個圖里面的PTPER就是我們說的ARR, PDC1,2就是我們說的CCR1,2,幾個通道就有幾個CCR,看圖計數值從0開始爬到PTPER,然后在爬升的過程中,PDC1遇到后,PMW1H就發生了一次翻轉,然后在計時器從PTPER下降的過程中,遇到了PDC1,PMW1H也發生了一次翻轉,這樣這個PMW1H通道就在一個周期T內發生了兩次狀態改變,1-變到0-變到1,這里的T就是計數器從0爬到PTPER再降低到0的這個過程的時間;那么再看,你改變了CCR值也就是圖8的PDC1, 2值,是不是就能實現控制了PWM1H, PWM2H的波形了,這個波形最終是產生出來我們上文提到的24°或者其他方向的一個確定模長電壓矢量;
FOC周期和這個PWM周期T怎么理解呢 , 一般來看 :
FOC的運算要在這個PWM內做出改變CCR值,也就是圖8的這個PDC1,2值,
有的人呢會在一個PWM周期內,做兩次FOC,也就是每一半的PWM周期內,它都會計算出一個新的CCR值,然后在下半個PWM周期開始的時候就應用了這個新CCR值,這種就是FOC頻率是PWM頻率的兩倍,
有的人是一個PWM周期內,做一次FOC,這樣FOC頻率就和PWM頻率一樣了,
有的人呢是多次PWM周期內,才做一次FOC,這樣呢就是FOC頻率比PWM頻率低了,
但是FOC頻率最快,也不會比PWM頻率高出一倍,那是極限了,否則FOC計算出來的CCR值沒辦法在PWM內得到有效的應用
圖8的這種中心對稱是可以的,對稱中心PWM1H,2H都是00的狀態,我們也有別的方案的中心對稱,我這里就使用對稱中心是1,1的狀態;
我們繼續回到兩個Udc的非零矢量合成24°方向的矢量的問題:
解釋了T的含義了,然后我們看t1,t2多大,我們根據這個矢量的合成,列出一個公式,看圖7,為了方便閱讀,我這里再插入圖7:

圖7

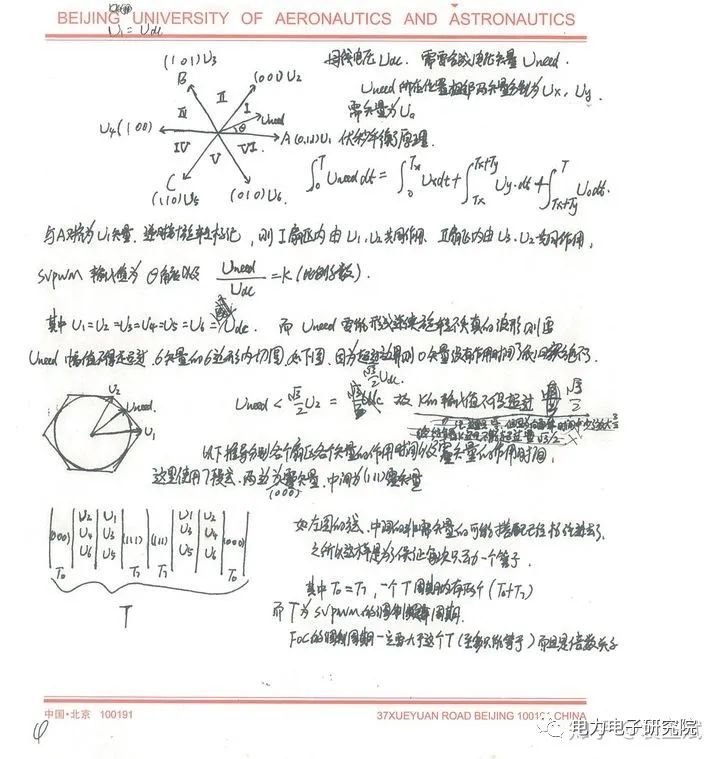



最后的結論就是:給定一個角度,和幅度的電壓矢量,可以獲得對應的單片機的三個定時器通道的CCR值,
這里補充一點,草稿中的P1和P2是指對應兩個非零矢量在一個7段式的周期里面,分別工作的總時間,為什么說總,因為中心對稱,前后各一半;PHA,PHB,PHC就是對應的定時器的ABC通道從哪個計數值開始翻轉的意思;
其實到了這里,有心的朋友完全可以自己推導出來一個極坐標下的svpwm生成的函數了,
alpha和beta的坐標下的,實際是這個極坐標下的計算中的一個中間過程,可以從極坐標的程序中化簡推導出來的,
這里用極坐標,是為了方便后續直觀的看到一個旋轉電壓矢量的作用效果的!
真的做FOC,你還是需要alpha和beta輸入的svpwm函數;
PS.( 上面的手稿中推導的式7段式的svpwm,為什么說式7段式,因為你看手稿第四頁啊,我的每個扇區的情況中都做了8段分割,而最中間的是1,1,1(從上往下看),我給分了兩次,這是為了好計算理解用的,實際是因為是一樣的狀態,所以其實有7個段,所以這叫做7段式,同理,如果你把中間的1,1,1全部摘掉,這樣原來1,1,1,兩端的矢量是不是可以直接推一起了,拿手稿第四頁的第一扇區舉例子,中間是不是就變成了U1在一起,這樣一下子少了兩段,所以就變5段式了,對應的時間公式,你看利用P1,P2是不是還是很容易就能計算出來了;這里我們一般5段式會摘掉1,1,1留下0,0,0是為了方便下橋臂電流采樣,和降低上橋臂的柵極驅動器的自舉負擔,這樣顯然也會導致下橋臂的負擔多些,你當然可以摘掉0,0,0只留1,1,1,你還可以周期性的0,0,0和1,1,1一個來一次。 )
-
磁場
+關注
關注
3文章
882瀏覽量
24266 -
矢量
+關注
關注
0文章
95瀏覽量
23760 -
繞組
+關注
關注
2文章
524瀏覽量
19919 -
FOC
+關注
關注
20文章
324瀏覽量
42894
發布評論請先 登錄
相關推薦
DSP電控成長之路
電機:交流感應電機FOC、無傳感器FOC和觀測器的介紹
【硬聲推薦】電機FOC控制視頻合集
電機控制--FOC的優勢





 電控入門之電機FOC
電控入門之電機FOC











評論