同圖像灰度不同，邊界處一般會(huì)有明顯的邊緣，利用此特征可以分割圖像。需要說(shuō)明的是：邊緣和物體間的邊界并不等同，邊緣指的是圖像中像素的值有突變的地方，而物體間的邊界指的是現(xiàn)實(shí)場(chǎng)景中的存在于物體之間的邊界。有可能有邊緣的地方并非邊界，也有可能邊界的地方并無(wú)邊緣，因?yàn)楝F(xiàn)實(shí)世界中的物體是三維的，而圖像只具有二維信息，從三維到二維的投影成像不可避免的會(huì)丟失一部分信息；另外，成像過(guò)程中的光照和噪聲也是不可避免的重要因素。正是因?yàn)檫@些原因，基于邊緣的圖像分割仍然是當(dāng)前圖像研究中的世界級(jí)難題，目前研究者正在試圖在邊緣提取中加入高層的語(yǔ)義信息。

在實(shí)際的圖像分割中，往往只用到一階和二階導(dǎo)數(shù)，雖然，原理上，可以用更高階的導(dǎo)數(shù)，但是，因?yàn)樵肼暤挠绊懀诩兇舛A的導(dǎo)數(shù)操作中就會(huì)出現(xiàn)對(duì)噪聲的敏感現(xiàn)象，三階以上的導(dǎo)數(shù)信息往往失去了應(yīng)用價(jià)值。二階導(dǎo)數(shù)還可以說(shuō)明灰度突變的類型。在有些情況下，如灰度變化均勻的圖像，只利用一階導(dǎo)數(shù)可能找不到邊界，此時(shí)二階導(dǎo)數(shù)就能提供很有用的信息。二階導(dǎo)數(shù)對(duì)噪聲也比較敏感，解決的方法是先對(duì)圖像進(jìn)行平滑濾波，消除部分噪聲，再進(jìn)行邊緣檢測(cè)。不過(guò)，利用二階導(dǎo)數(shù)信息的算法是基于過(guò)零檢測(cè)的，因此得到的邊緣點(diǎn)數(shù)比較少，有利于后繼的處理和識(shí)別工作。

各種算子的存在就是對(duì)這種導(dǎo)數(shù)分割原理進(jìn)行的實(shí)例化計(jì)算，是為了在計(jì)算過(guò)程中直接使用的一種計(jì)算單位。

1.Sobel算子

其主要用于邊緣檢測(cè)，在技術(shù)上它是以離散型的差分算子，用來(lái)運(yùn)算圖像亮度函數(shù)的梯度的近似值， Sobel算子是典型的基于一階導(dǎo)數(shù)的邊緣檢測(cè)算子，由于該算子中引入了類似局部平均的運(yùn)算，因此對(duì)噪聲具有平滑作用，能很好的消除噪聲的影響。Sobel算子對(duì)于象素的位置的影響做了加權(quán)，與Prewitt算子、Roberts算子相比因此效果更好。

Sobel算子包含兩組3x3的矩陣，分別為橫向及縱向模板，將之與圖像作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。實(shí)際使用中，常用如下兩個(gè)模板來(lái)檢測(cè)圖像邊緣。

檢測(cè)水平邊沿 橫向模板 ：

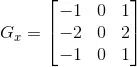
檢測(cè)垂直平邊沿 縱向模板：

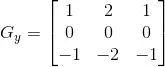
圖像的每一個(gè)像素的橫向及縱向梯度近似值可用以下的公式結(jié)合，來(lái)計(jì)算梯度的大小。

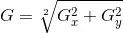
然后可用以下公式計(jì)算梯度方向。

在以上例子中，如果以上的角度Θ等于零，即代表圖像該處擁有縱向邊緣，左方較右方暗。

缺點(diǎn)是Sobel算子并沒(méi)有將圖像的主題與背景嚴(yán)格地區(qū)分開(kāi)來(lái)，換言之就是Sobel算子并沒(méi)有基于圖像灰度進(jìn)行處理，由于Sobel算子并沒(méi)有嚴(yán)格地模擬人的視覺(jué)生理特征，所以提取的圖像輪廓有時(shí)并不能令人滿意。

2. Isotropic Sobel算子

Sobel算子另一種形式是(Isotropic Sobel)算子，加權(quán)平均算子，權(quán)值反比于鄰點(diǎn)與中心點(diǎn)的距離，當(dāng)沿不同方向檢測(cè)邊緣時(shí)梯度幅度一致，就是通常所說(shuō)的各向同性Sobel(Isotropic Sobel)算子。模板也有兩個(gè)，一個(gè)是檢測(cè)水平邊沿的 ，另一個(gè)是檢測(cè)垂直平邊沿的 。各向同性Sobel算子和普通Sobel算子相比，它的位置加權(quán)系數(shù)更為準(zhǔn)確，在檢測(cè)不同方向的邊沿時(shí)梯度的幅度一致。

3.Roberts算子

羅伯茨算子、Roberts算子是一種最簡(jiǎn)單的算子，是一種利用局部差分算子尋找邊緣的算子，他采用對(duì)角線方向相鄰兩象素之差近似梯度幅值檢測(cè)邊緣。檢測(cè)垂直邊緣的效果好于斜向邊緣，定位精度高，對(duì)噪聲敏感,無(wú)法抑制噪聲的影響。1963年，Roberts提出了這種尋找邊緣的算子。

Roberts邊緣算子是一個(gè)2x2的模板，采用的是對(duì)角方向相鄰的兩個(gè)像素之差。從圖像處理的實(shí)際效果來(lái)看，邊緣定位較準(zhǔn)，對(duì)噪聲敏感。適用于邊緣明顯且噪聲較少的圖像分割。Roberts邊緣檢測(cè)算子是一種利用局部差分算子尋找邊緣的算子,Robert算子圖像處理后結(jié)果邊緣不是很平滑。經(jīng)分析，由于Robert算子通常會(huì)在圖像邊緣附近的區(qū)域內(nèi)產(chǎn)生較寬的響應(yīng)，故采用上述算子檢測(cè)的邊緣圖像常需做細(xì)化處理，邊緣定位的精度不是很高。

4. Prewitt算子

Prewitt算子是一種一階微分算子的邊緣檢測(cè)，利用像素點(diǎn)上下、左右鄰點(diǎn)的灰度差，在邊緣處達(dá)到極值檢測(cè)邊緣，去掉部分偽邊緣，對(duì)噪聲具有平滑作用 。其原理是在圖像空間利用兩個(gè)方向模板與圖像進(jìn)行鄰域卷積來(lái)完成的，這兩個(gè)方向模板一個(gè)檢測(cè)水平邊緣，一個(gè)檢測(cè)垂直邊緣。

對(duì)數(shù)字圖像f(x，y)，Prewitt算子的定義如下：

G(i)=|[f(i-1,j-1)+f(i-1,j)+f(i-1，j+1)]-[f(i+1,j-1)+f(i+1，j)+f(i+1，j+1)]|

G(j)=|[f(i-1,j+1)+f(i,j+1)+f(i+1，j+1)]-[f(i-1,j-1)+f(i,j-1)+f(i+1，j-1)]|

則 P(i,j)=max[G(i),G(j)]或 P(i,j)=G(i)+G(j)

經(jīng)典Prewitt算子認(rèn)為：凡灰度新值大于或等于閾值的像素點(diǎn)都是邊緣點(diǎn)。即選擇適當(dāng)?shù)拈撝礣，若P(i,j)≥T，則(i,j)為邊緣點(diǎn)，P(i,j)為邊緣圖像。這種判定是欠合理的，會(huì)造成邊緣點(diǎn)的誤判，因?yàn)樵S多噪聲點(diǎn)的灰度值也很大，而且對(duì)于幅值較小的邊緣點(diǎn)，其邊緣反而丟失了。

Prewitt算子對(duì)噪聲有抑制作用，抑制噪聲的原理是通過(guò)像素平均，但是像素平均相當(dāng)于對(duì)圖像的低通濾波，所以Prewitt算子對(duì)邊緣的定位不如Roberts算子。

因?yàn)槠骄軠p少或消除噪聲，Prewitt梯度算子法就是先求平均，再求差分來(lái)求梯度。水平和垂直梯度模板分別為：

檢測(cè)水平邊沿 橫向模板 ：

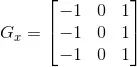
檢測(cè)垂直平邊沿 縱向模板：

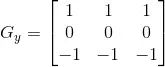
該算子與Sobel算子類似，只是權(quán)值有所變化，但兩者實(shí)現(xiàn)起來(lái)功能還是有差距的，據(jù)經(jīng)驗(yàn)得知Sobel要比Prewitt更能準(zhǔn)確檢測(cè)圖像邊緣。

5.Laplacian算子

Laplace算子是一種各向同性算子，二階微分算子，在只關(guān)心邊緣的位置而不考慮其周圍的象素灰度差值時(shí)比較合適。Laplace算子對(duì)孤立象素的響應(yīng)要比對(duì)邊緣或線的響應(yīng)要更強(qiáng)烈，因此只適用于無(wú)噪聲圖象。存在噪聲情況下，使用Laplacian算子檢測(cè)邊緣之前需要先進(jìn)行低通濾波。所以，通常的分割算法都是把Laplacian算子和平滑算子結(jié)合起來(lái)生成一個(gè)新的模板。

拉普拉斯算子也是最簡(jiǎn)單的各向同性微分算子，具有旋轉(zhuǎn)不變性。一個(gè)二維圖像函數(shù)的拉普拉斯變換是各向同性的二階導(dǎo)數(shù)，定義了更適合于數(shù)字圖像處理，將拉式算子表示為離散形式：

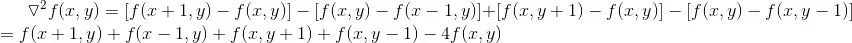
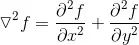
另外，拉普拉斯算子還可以表示成模板的形式，如下圖所示，

離散拉普拉斯算子的模板：

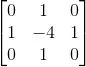
其擴(kuò)展模板：

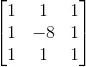
拉式算子用來(lái)改善因擴(kuò)散效應(yīng)的模糊特別有效，因?yàn)樗辖抵颇Ｐ汀U(kuò)散效應(yīng)是成像過(guò)程中經(jīng)常發(fā)生的現(xiàn)象。

Laplacian算子一般不以其原始形式用于邊緣檢測(cè)，因?yàn)槠渥鳛橐粋€(gè)二階導(dǎo)數(shù)，Laplacian算子對(duì)噪聲具有無(wú)法接受的敏感性；同時(shí)其幅值產(chǎn)生算邊緣，這是復(fù)雜的分割不希望有的結(jié)果；最后Laplacian算子不能檢測(cè)邊緣的方向；所以Laplacian在分割中所起的作用包括：（1）利用它的零交叉性質(zhì)進(jìn)行邊緣定位；（2）確定一個(gè)像素是在一條邊緣暗的一面還是亮的一面；一般使用的是高斯型拉普拉斯算子（Laplacian of a Gaussian,LoG)，由于二階導(dǎo)數(shù)是線性運(yùn)算，利用LoG卷積一幅圖像與首先使用高斯型平滑函數(shù)卷積改圖像，然后計(jì)算所得結(jié)果的拉普拉斯是一樣的。所以在LoG公式中使用高斯函數(shù)的目的就是對(duì)圖像進(jìn)行平滑處理，使用Laplacian算子的目的是提供一幅用零交叉確定邊緣位置的圖像；圖像的平滑處理減少了噪聲的影響并且它的主要作用還是抵消由Laplacian算子的二階導(dǎo)數(shù)引起的逐漸增加的噪聲影響。

6.Canny算子

該算子功能比前面幾種都要好，但是它實(shí)現(xiàn)起來(lái)較為麻煩，Canny算子是一個(gè)具有濾波，增強(qiáng)，檢測(cè)的多階段的優(yōu)化算子，在進(jìn)行處理前，Canny算子先利用高斯平滑濾波器來(lái)平滑圖像以除去噪聲，Canny分割算法采用一階偏導(dǎo)的有限差分來(lái)計(jì)算梯度幅值和方向，在處理過(guò)程中，Canny算子還將經(jīng)過(guò)一個(gè)非極大值抑制的過(guò)程，最后Canny算子還采用兩個(gè)閾值來(lái)連接邊緣。

Canny邊緣檢測(cè)算法

step1:用高斯濾波器平滑圖象；

step2:用一階偏導(dǎo)的有限差分來(lái)計(jì)算梯度的幅值和方向；

step3:對(duì)梯度幅值進(jìn)行非極大值抑制

step4:用雙閾值算法檢測(cè)和連接邊緣

(1)圖象邊緣檢測(cè)必須滿足兩個(gè)條件：一能有效地抑制噪聲；二必須盡量精確確定邊緣的位置。

(2)根據(jù)對(duì)信噪比與定位乘積進(jìn)行測(cè)度，得到最優(yōu)化逼近算子。這就是Canny邊緣檢測(cè)算子。

(3)類似與Marr（LoG）邊緣檢測(cè)方法，也屬于先平滑后求導(dǎo)數(shù)的方法。

審核編輯：湯梓紅