浮點數
考慮如下一段代碼:
// Java
public class Example {
public static void main(String[] args) {
int i = 12345;
float f = 12345.0F;
System.out.printf("binary str of i: %s\\n", int2BinaryStr(i));
System.out.printf("binary str of f: %s\\n", float2BinaryStr(f));
}
// 將int轉為32位的二進制表示
private static String int2BinaryStr(int i) {
String str = Integer.toBinaryString(i);
for (int len = str.length(); len < 32; len++) {
str = "0" + str;
}
return str;
}
// 將float轉為32位的二進制表示
private static String float2BinaryStr(float f) {
return int2BinaryStr(Float.floatToRawIntBits(f));
}
}
我們將整數 i = 12345 和 浮點數 f = 12345.0 轉成二進制表示,結果如下:
binary str of i: 00000000000000000011000000111001
binary str of f: 01000110010000001110010000000000
雖然從十進制上看,值都是 12345,但是兩種類型的二進制表示卻差別很大,說明, 計算機系統對整數和浮點數的處理是兩套不同的機制 。
大部分編程語言支持的整數最大是 64 位,但很多場景下,我們需要更大的取值范圍,或者是小數運算,這些都是 64 位整數無法滿足的場景。為了解決這些,計算機系統引入了 浮點數 ( Floating Point )類型。
浮點數類型可以分為 32 位單精度 float/float32 類型和 64 位雙精度 double/float64 類型,取值范圍如下:
| 類型 | 最小值 | 最大值 |
|---|---|---|
| float | -3.40282347E+38 | 3.40282347E+38 |
| double | -1.79769313486231570E+308 | 1.79769313486231570E+308 |
雖然浮點數的取值范圍很廣,但它只能精確表示其中一小部分,其他都是近似表示 。
下面,我們將深入介紹浮點數的二進制表示和近似規則。
簡單浮點數編碼
對于十進制數 ,可以表示成 ,其中,以小數點 為界,左邊為整數部分,右邊為小數部分,那么:
比如, 。
同理,對于二進制數 ,也可以表示成 ,同樣以小數點 分割整數和小數部分,那么:
比如,。
計算機系統的這種編碼方式,注定只能表示 形式的數,其他的,只能近似表示。
比如,無法精確表示 0.2:
| 二進制表示 | 分數 | 十進制表示 |
|---|---|---|
| 0.0 | 0/2 | 0.0 |
| 0.01 | 1/4 | 0.25 |
| 0.010 | 2/8 | 0.25 |
| 0.0011 | 3/16 | 0.1875 |
| 0.00110 | 6/32 | 0.1875 |
| 0.001101 | 13/64 | 0.203125 |
| 0.0011010 | 26/128 | 0.203125 |
| 0.00110011 | 51/256 | 0.19921875 |
浮點數除了表示小數之外,還須表示大數,按照這種二進制編碼思路,如果要表示 ,需要 102 位,受限于計算機系統的編碼長度,這顯然不能接受。
其實,對 形式的數,我們只須存儲 M 和 E 即可,再來一個符號位 s,即可表示這種形式的數: 。
對 w 位浮點數,可以用 1 位表示 s,用 k 位表示 E,用 n 位表示 M,那么就有 w = 1 + k + n:
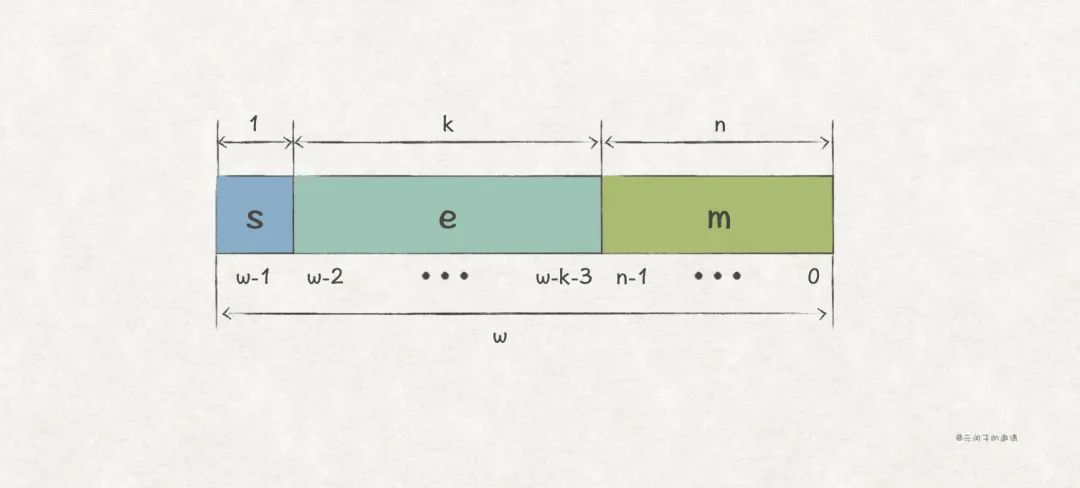
(1)s 的編碼
用 0 表示正數,1 表示負數。
(2)E 的編碼
二進制表示為 ,因為 E 可以是正,也可以是負,因此,可以直接用 補碼 進行編碼。
比如,k = 4 時,E 的取值是這樣的:
| e | E |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| ... | |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| ... | |
| 1111 | -1 |
但是,這樣從 到 并不是遞增的趨勢。另一種方法是,對 e 用無符號編碼,令 ,其中,。比如,k = 4 時,,那么 E 的取值是這樣的:
| e | Bias | E |
|---|---|---|
| 0000 | 7 | -7 |
| 0001 | 7 | -6 |
| ... | ||
| 0111 | 7 | 0 |
| 1000 | 7 | 1 |
| 1001 | 7 | 2 |
| ... | ||
| 1111 | 7 | 8 |
(3)M 的編碼
二進制表示為 ,M 不涉及負數,因此可以只用最高位表示整數,其他表示小數,即 。比如,當 n = 3 時,M 的取值如下:
| m | M | 十進制 |
|---|---|---|
| 000 | 0.00 | 0.00 (0/4) |
| 001 | 0.01 | 0.25 (1/4) |
| 010 | 0.10 | 0.5 (2/4) |
| 011 | 0.11 | 0.75 (3/4) |
| 100 | 1.00 | 1.00 (4/4) |
| 101 | 1.01 | 1.25 (5/4) |
| 110 | 1.10 | 1.5 (6/4) |
| 111 | 1.11 | 1.75 (7/4) |
但是, 這種編碼方式會導致 0 有很多種表示 。比如 w = 8,k = 4,n = 3 時,因為 ,所以 、、 等的浮點數值都是 0。
可以這么改動,令 ,當 時,;當 時,:
| e | m | M | 十進制 |
|---|---|---|---|
| 0000 | 000 | 0.000 | 0.000 (0/8) |
| 0000 | 001 | 0.001 | 0.125 (1/8) |
| ... | |||
| 0000 | 111 | 0.111 | 0.875 (7/8) |
| 0001 | 000 | 1.000 | 1.000 (8/8) |
| 0001 | 1.001 | 1.125 (9/8) | |
| ... |
這樣,既解決了 0 的表示問題,又讓 M 的精度更大了 。
IEEE 浮點數編碼
上述這些編碼方法,就是 IEEE 754 Floating-Point Representation 標準中定義的浮點數編碼方式的基本思路,標準會在此基礎上做了一些調整,比如新增了 Infinity 和 NaN 的表示。
IEEE 標準將浮點數分成 單精度 和 雙精度 兩種,分別用 32 位和 64 位表示,它們的 k 值和 n 值都不同:

在此基礎上,根據 e 的取值不同,又分為 3 種場景, Denormalized Values 、 Normalized Values 、 Special Values :
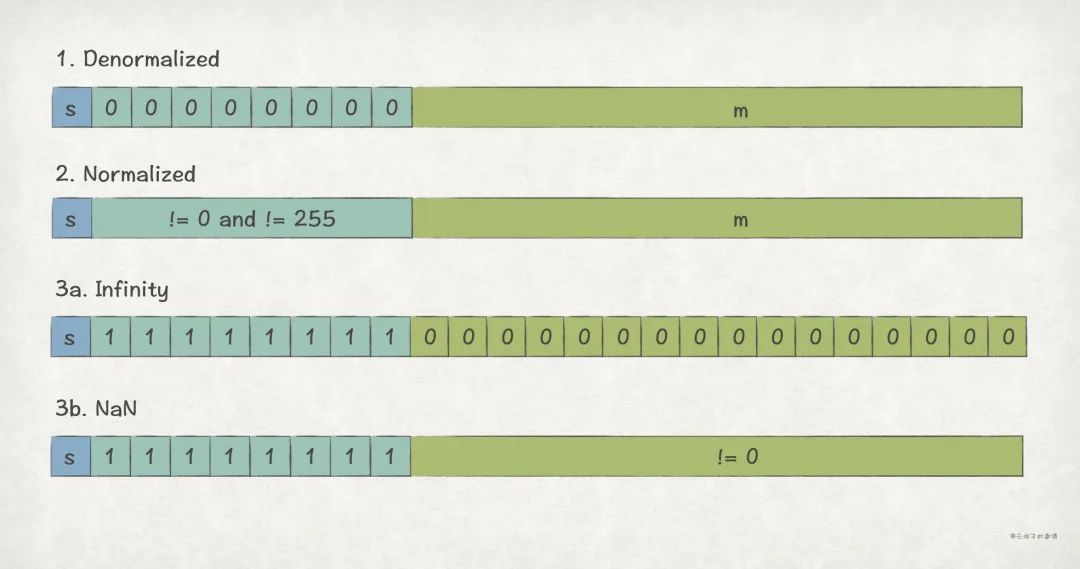
(1)Denormalized Values
此場景下,e 取值為全 0, 用來表示 0 值,以及接近 0 的小數 。
在 的表示下,,。
為什么 ,而不是 E = -Bias ?
根據前文分析,應該有 E = e - Bias,但 Denormalized Values 中,確是 E = 1 - Bias,而不是 E = 0 - Bias。
這主要考慮到,從 Denormalized Values 到 Normalized Values 的平滑過度,讓 Largest Denormalized Value 和 Smallest Normalized Value 更接近。后面的舉例可以看到。
這里,0 分為了 -0.0 和 +0.0,在一些科學計算場景下,它們會表示不同的含義。比如 ,。
(2) Normalized Values
此場景下,e 取值不是全 0,也不是全 1,是最常見的場景。
在 的表示下,,。
(3)Special Values
此場景下,e 取值為全 1,用來表示 Infinity 和 NaN。
- m 取值全 0,表示 Infinity:1)s = 0 時,為 ;2)s = 1 時,為 。
- m 取值不是全 0,表示 NaN(Not a Number),比如 或者 。
比如,w = 8,k = 4(此時,),n = 3 時,IEEE 標準浮點數的編碼例子如下:
| 場景 | 二進制 | e | E | m | M | 十進制 | ||
|---|---|---|---|---|---|---|---|---|
| Denormalized | 0 0000 000 | 0 | -6 | 1/64 | 0/8 | 0/8 | 0/512 | 0.0 |
| 0 0000 001 | 0 | -6 | 1/64 | 1/8 | 1/8 | 1/512 | 0.001953 | |
| ... | ||||||||
| 0 0000 111 | 0 | -6 | 1/64 | 7/8 | 7/8 | 7/512 | 0.013672 | |
| Normalized | 0 0001 000 | 1 | -6 | 1/64 | 0/8 | 8/8 | 8/512 | 0.015625 |
| 0 0001 001 | 1 | -6 | 1/64 | 1/8 | 9/8 | 9/512 | 0.017578 | |
| ... | ||||||||
| 0 1110 111 | 14 | 7 | 128 | 7/8 | 15/8 | 1920/8 | 240.0 | |
| Infinity | 0 1111 000 | - | - | - | - | - | - | |
| NaN | 0 1111 001 | - | - | - | - | - | - | NaN |
| ... | NaN |
從上表可以看出,因為 Denormalized 場景下令 E = 1 - Bias,從 Denormalized 到 Normalized 的過度,也即 7/512 到 8/512,更平滑了。如果令 E = - Bias,則是從 7/1024 到 8/512,跨度太大。
到這里,我們已經深入介紹了 IEEE 浮點數編碼格式,回到本節最開始的例子,如何從 int i = 12345 的二進制表示,推斷出 float f = 12345.0 的二進制表示?
- 首先,12345 整數的二進制表示為 ,也可以表示成 ,對應到 的形式,可以確認 s = 0,E = 13,M = 1.1000000111001。
- 另外,12345 屬于 Normalized 場景,而 float 類型中 k = 8,有,,得出 e = 140,按 k 位無符號編碼表示為 。
- 同理,由 ,float 類型中,n = 23,所以,得出 m 的二進制表示為 ,注意, 低位補零 。
- 最后將 s、e、m 按照 float 單精度的編碼格式組合起來,就是 ,也即 12345.0 的二進制編碼。
近似規則(Rounding)
前面說過,浮點數只能表示 形式的數,其他的,只能近似表示。
近似規則,我們最熟悉的是 “ 四舍五入 ”,比如,要保留 2 位小數,那么 1.234、1.235、1.236 近似之后分別是 1.23、1.24、1.24。
IEEE 浮點數標準中,并沒采用 “四舍五入” 法,定義了如下 4 種近似規則:
- Round-to-even ,往更近的方向靠,如果向上和向下的距離一樣,則往偶數的方向靠。
- Round-toward-zero ,往 0 的方向靠。
- Round-down ,往更小的方向靠。
- Round-up ,往更大的方向靠。
比如,下面的例子,需要近似為整數:
| 規則 | 1.40 | 1.60 | 1.50 | 2.50 | -1.50 |
|---|---|---|---|---|---|
| Round-to-even | 1 | 2 | 2 | 2 | -2 |
| Round-toward-zero | 1 | 1 | 1 | 2 | -1 |
| Round-down | 1 | 1 | -2 | ||
| Round-up | 2 | 2 | 3 | -1 |
這些規則對二進制也生效,比如,Round-to-even 規則,在二進制中,0 代表偶數,1 表示奇數。下面例子中,需要按照 Round-to-even 近似保留 2 位小數:
| 二進制(十進制) | 向下 | 中點 | 向上 | Round-to-even |
|---|---|---|---|---|
| 10.00011 (67/32) | 10.00 (64/32) | 68/32 | 10.01 (72/32) | 10.00 (64/32) |
| 10.00110 (70/32) | 10.00 (64/32) | 68/32 | 10.01 (72/32) | 10.01 (72/32) |
| 10.11100 (23/8) | 10.11 (22/8) | 23/8 | 11.00 (24/8) | 11.00 (24/8) |
| 10.10100 (21/8) | 10.10 (20/8) | 21/8 | 10.11 (22/8) | 10.10 (20/8) |
上述例子中,前 2 個按照就近原則近似;后 2 個處于中點位置,往偶數方向靠。
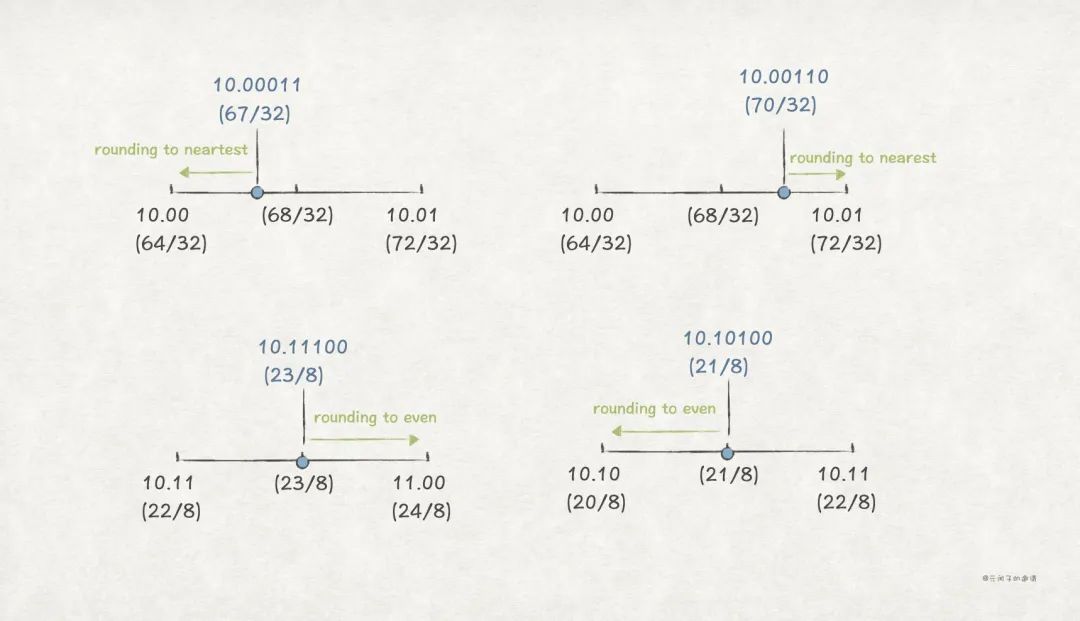
注意, IEEE 標準規定 Round-to-even 為默認的近似規則 。
浮點數運算
浮點數的運算規則比較簡單,令 指代后一類的運算符,x 和 y 為浮點數類型,那么 的運算結果為 ,也即對真實計算結果進行近似。
注意,算術運算的 結合律 、分配率在浮點數運算下是不生效的,比如:
// Java
public static void main(String[] args) {
// 結合律不滿足示例
float f1 = 3.14F;
float f2 = 1e10F;
float f3 = (f1 + f2) - f2;
float f4 = f1 + (f2 - f2);
System.out.printf("(3.14 + 1e10) - 1e10 = %f\\n", f3);
System.out.printf("3.14 + (1e10 - 1e10) = %f\\n", f4);
// 分配律不滿足示例
float f5 = 1e20F;
float f6 = f5 * (f5 - f5);
float f7 = f5 * f5 - f5 * f5;
System.out.printf("1e20 * (1e20 - 1e20) = %f\\n", f6);
System.out.printf("1e20 * 1e20 - 1e20 * 1e20 = %f\\n", f7);
}
// 輸出結果
(3.14 + 1e10) - 1e10 = 0.000000
3.14 + (1e10 - 1e10) = 3.140000
1e20 * (1e20 - 1e20) = 0.000000
1e20 * 1e20 - 1e20 * 1e20 = NaN
結合律例子中,(3.14+1e10)-1e10 結果是 0,因為 3.14 在近似時,精度丟失了,也即 3.14+1e10=1e10;類似,分配律例子中,1e20*1e20 的結果超出了 float 類型的表示范圍,得到 Infinity,而 Infinity - Infinity 的結果是 NaN。
注意, 浮點數運算結果,如果超出了浮點數表示范圍,會得到 Infinity/-Infinity 。這與整數運算的溢出機制有所區別。
-
二進制
+關注
關注
2文章
796瀏覽量
41741 -
計算機
+關注
關注
19文章
7534瀏覽量
88502 -
編程
+關注
關注
88文章
3637瀏覽量
93924
發布評論請先 登錄
相關推薦
簡單介紹微型計算機的組成
深入理解計算機系統的數值類型
計算機系統對數值類型的編碼、運算、轉換原理介紹1
計算機系統對數值類型的編碼、運算、轉換原理介紹2

計算機系統對數值類型的編碼、運算、轉換原理介紹4





 計算機系統對數值類型的編碼、運算、轉換原理介紹3
計算機系統對數值類型的編碼、運算、轉換原理介紹3










評論