這是一篇關于模擬高斯濾波器設計的經典文章，發表于1959年1月的《電氣通信》雜志上。此篇文章引用度比較高，而且內容非常詳實，包含了高斯濾波器綜合和實現的整個過程，文章中也討論了有限Q值的濾波器設計非常有參考價值。

在過去的三十多年里，濾波器的設計一直遵循鏡像參數法(the image-parameter theory)。這種理論在商業中得到了廣泛應用，很大程度上是因為大多數濾波器只需要滿足近似的性能要求。在需要更精確特性的場合，通常只需在實際濾波器中調整元件值，就能得到可接受的設計。然而，要實現通帶內精確的幅度和相位響應，基于鏡像參數法的簡單近似就不再適用，需要使用基于現代網絡理論(modern network theory, 即插入損耗法)的方法來解決。

現代網絡理論是基爾霍夫定律(Kirchhoff's laws)在濾波器參數計算中的優雅擴展。從所需濾波器的幅度、相位或時間響應的預定指標出發，方程會計算出必須包含在濾波器中的每個元件的精確值，而不受鏡像參數法的固有限制，即在物理上不實際的終端阻抗和無耗電抗。

十多年前，關于現代網絡理論的濾波器設計的一系列實用論文中的第一篇發表在《電氣通信》(Electrical Communication)上。本期還有一篇關于這個系列的文章。

譯注：這里說的十多年前的文章主要由Vitold Belevitch所貢獻，可以參考：https://en.wikipedia.org/wiki/Vitold_Belevitch

Gaussian-Response Filter Design

高斯響應濾波器設計

By MILTON DISHAL

ITT Laboratories, a division of International Telephone and Telegraph Corporation; Nutley, New Jersey

具有高斯響應特性的濾波器在脈沖系統中非常有用，因為它們在快速信號變化后產生的波形過沖和振鈴很小。本文首先概述了理想高斯濾波器的幅度、相位、脈沖響應、階躍響應和有效熱噪聲帶寬。接下來給出了一種物理可實現的幅度特性逼近。并提供了這種逼近的復頻率根(最高到9階)。然后，按綜合復雜度的順序，考慮了使用這些根來設計分段調諧系統、僅一端有阻性負載的無耗和均勻有耗濾波器，以及兩端均有阻性負載的同樣的濾波器；所有設計都提供了階高斯幅度逼近。數值設計數據提供在7個表格中；并給出了一個低通和一個帶通設計實例。

在許多通信系統中，特別是涉及脈沖的系統，希望系統響應幅度隨帶寬(response-magnitude-versus-bandwidth)變化特性呈高斯形狀(譯注：推導過程可以參考和ChatGPT聊聊高斯濾波器設計)。

本文沒有考慮這個問題的系統方面，但可以提到的是，使用高斯響應形狀的一些有益的定性結果是在快速信號變化后產生的過沖和振鈴非常小，以及在施加脈沖時可以獲得的對稱脈沖輸出。

本文旨在提供精確數據，使得能夠成功設計和構建具有幅度與頻率特性為階理想高斯幅度響應逼近的低通和帶通濾波器，其中是整個濾波器中的元件數量(在低通濾波器中，元件表示電抗(reactances)；在帶通濾波器中，表示諧振器(resonators))。正如后面一節所示，產生理想高斯響應需要無限數量的元件，因此在使用有限數量的元件時，只能逼近這種響應。

1. 理想高斯響應特性

為了便于參考，本節簡要介紹了理想高斯響應的五個經常用到的特性。

1.1 相對衰減幅度與帶寬的關系

方程(1)給出了理想高斯相對衰減幅度的表達式：

譯注：這里的系數0.3466是這樣算出來的，令，即讓其傳遞函數的3dB截止頻率處功率衰減一半。解得，這里和下述公式中的相同，下式是系統傳遞函數：

其中 是濾波器在零帶寬時的峰值輸出電壓， 是任意帶寬 下的輸出電壓， 是帶寬值(低通情況下為實際弧度頻率，對稱載波中心帶通情況下為總帶寬)。 是歸一化帶寬，通常可以從它所在的方程中推導出其意義。例如，繪制(1)的圖像可以發現，當 時，相對衰減為1奈培(neper)或8.68dB。從同一相對衰減圖中可以看出，，經過重新歸一化至3dB帶寬后，得到(1)的第二個右側表達式。對(1)的兩側取，以獲得dB表示的簡單的相對衰減式(1A)：

譯注：這里式(1A)求解高斯濾波器衰減特性，對式(1)兩邊取得到:

在兩倍的3dB帶寬處，理想高斯相對衰減的幅度為12dB；在三倍的3dB帶寬處，為27dB；等等。

1.2 相對衰減相位(相位滯后)與帶寬的關系

基于表示幅度(1)所需的無窮項級數這一事實，可以證明理想高斯相位特性具有無限斜率，并且完全線性，如下式所示：

其中 是帶通響應中間或低通響應零頻率處的實際相移。相位特性的無限線性斜率導致通過理想高斯濾波器的信號具有無限時間延遲。通過有限數量的網絡元件對高斯響應進行逼近將導致有限的時間延遲。

譯注：這一小結容易產生疑惑，對于(1)式，實際上還包含一個虛部為0的項，即信號相位為0，得到結論，理想高斯濾波器對所有信號的相位移動都是0。但是為什么這里作者指出相位特性具有無限斜率，且對信號具有無限時間延遲呢？

這里可以這樣理解：實際上對于一個理想高斯濾波器，我們需要無窮多的元器件來綜合實現，比如如下這樣，

當輸入端輸入信號后，因為中間有無窮項，信號永遠也無法輸出！所以說理想高斯濾波器對信號具有無限時間延遲，也即得到相位的無限斜率特性。

1.3 脈沖響應與時間的關系

理想高斯濾波器的脈沖響應為：

譯注：時域脈沖響應可以使用頻域的反傅里葉變換求得：

其中所以這里的系數.

其中 是從脈沖響應中心的無限延遲處計算的時間差(正負)， 是任意時間 處的輸出， 是峰值輸出(在 時出現)。繪制(3)的圖像顯示，半幅度點之間的總時間寬度為，10%幅度的總時間寬度為，1%幅度的總時間寬度為，0.1%幅度的時間寬度為。其中， 是低通情況下的實際3dB截止頻率，對于對稱載波中心帶通情況， 是總3dB帶寬的一半。

1.4 階躍響應與時間的關系

理想高斯濾波器的階躍響應為：

譯注：階躍響應使用沖擊響應的積分求得：

其中，原文中的公式(4)是錯誤的。

其中是從階躍響應中間向上的無限延遲時間(正負)計算的時間差。繪制(4)時，可以看到10%至90%的上升時間等于0.344 /，5%至95%的上升時間等于0.437 /，其中是低通情況下的實際3dB截止頻率，對稱載波為中心的帶通情況下是總3dB帶寬的一半。

1.5 有效噪聲帶寬

為了計算無線電接收機的熱噪聲限制靈敏度，需要知道評估接收機選擇性的有效噪聲帶寬。對于歸一化高斯響應形狀，熱噪聲帶寬

有效熱噪聲帶寬是具有與實際電壓平方響應形狀相同的峰值響應和相同總面積的矩形電壓平方歸一化響應形狀的寬度。

2. 使用個網絡元件逼近高斯幅度特性

如前所述，要用多項式形式表示的無窮項數目的期望網絡功能，需要綜合一個包含無窮多元件的集總線性網絡。因此，在實際應用中需要對第1節中詳細介紹的理想高斯響應進行逼近。設計工程師必須決定需要逼近哪個特性，所逼近的特性有：幅度特性、相位特性、相位斜率特性(phase-slope)、脈沖響應特性、階躍響應特性等。本文討論的是高斯幅度特性的逼近問題。

2.1 相對衰減幅度的公式

正如很多次所提到的(例如，參見達林頓的論文)，一個由有限數量元件組成的集總線性網絡，在通帶之外產生持續增加的衰減，其相對衰減幅度公式如下：

是歸一化帶寬變量的最高次冪為的多項式，其中是網絡元件的數量，是該多項式在帶寬最小值處的數值。通過從多項式的常數項中減去并加上，顯然可以將(5)寫成以下形式：

因此，為了將期望的高斯相對衰減幅度方程(1)與物理可實現的網絡聯系起來，需要對(1)的平方求級數，而不是直接對(1)求級數，因為(5)表明，如果要將多項式中的項數與網絡中的元件數關聯起來，必須使用相對衰減幅度的平方。

譯注：這里作者將衰減曲線對曲線的最小值做了歸一化處理，這樣就將衰減方程寫成了:

的形式，也就是說這節的重點是現在所謂的特征函數(The Characteristic Function)。感興趣的同學可以參考《濾波器設計的逼近方法 - Butterworth, Chebyshev, Elliptic》。文中寫到"必須使用相對衰減幅度的平方"才能獲得實際元件值，這個說法通俗的解釋是由于實際器件都是正實數，而(1)式只能包含左半邊平面極點的函數，解出來的會存在虛數，而平方后，這些虛數都變為實數，就可以和實際器件形成對應關系了。

2.2 幅度逼近的結果

當上述平方之后，然后使用已知的收斂無窮級數，我們得到:

根據(5)關于多項式最高次冪的說明，可以看出，兩元件(低通電路的電抗；帶通電路的諧振器)濾波器可以滿足(6)的前三項，三元件濾波器可以滿足前四項，依此類推。一般來說，個元件的濾波器可以滿足(6)的前項。

在數學上有許多不同的方法來指定對期望曲線的最佳逼近；在本文中，所采用的逼近方法是盡可能滿足式(6)中的實際數值系數。

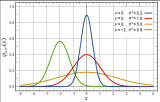
現在可以繪制用個元件所構成濾波器網絡獲得的高斯幅度逼近的曲線。圖1顯示了3dB截止點內的曲線部分，圖2顯示了3dB截止點外的曲線部分，這些曲線是包含多達10個元件的濾波器網絡的結果。在繪制之后，我們還記錄了的關系，并將所有曲線重新歸一化到它們自己的3dB截止點。從這些曲線中，工程師可以輕松確定滿足預定指標逼近所需的網絡元件數量。從圖2中，應注意到一個重要的事實：濾波器中使用的元件數量決定了逼近滿足理想高斯響應的相對衰減曲線(即相對響應曲線)的程度；例如，一個四元件濾波器可以在大約11dB點附近逼近高斯響應，誤差在1dB以內；6個元件則在大約18dB；8個元件在大約26dB；10個元件在大約34dB；如此等等。

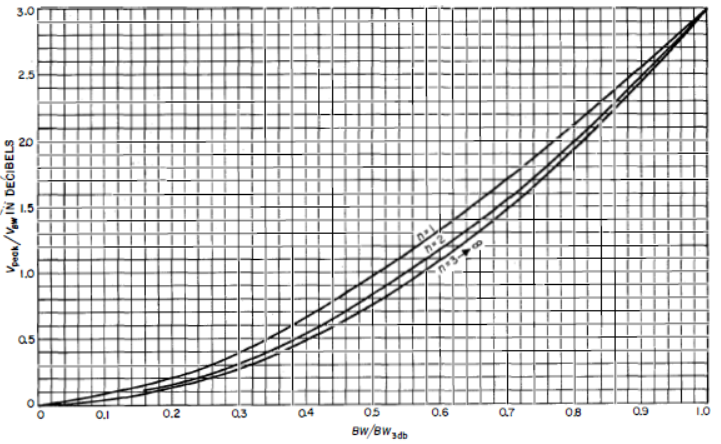
圖1-在3dB截止點以內的階高斯幅度逼近濾波器的相對衰減曲線。濾波器中的元件數量。

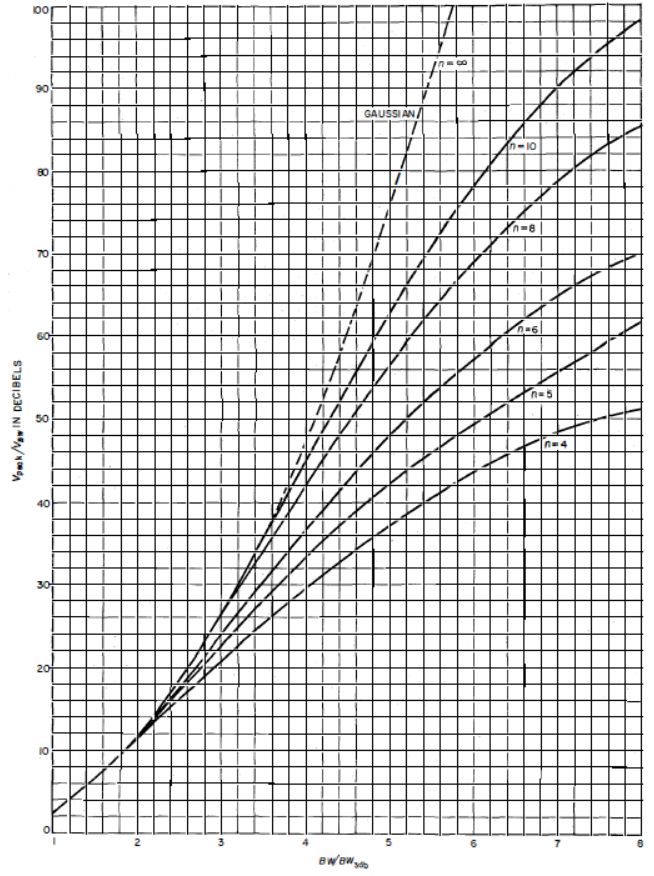
圖2-在3dB截止點以外的階高斯幅度逼近濾波器的相對衰減曲線。

理想高斯響應需要多大程度上逼近才行？這是一個重要的問題，取決于特定系統的要求，這個問題不在本文的討論范圍之內。

3. 高斯幅度逼近的復根及其在參差調諧放大器(Stagger-Tuned Amplifier)設計中的應用

當綜合一個網絡以產生精確所規定的連續增加的衰減幅度時，總是需要解出其衰減方程的個根，其中是多項式的最高次冪，也是濾波器中必須使用的元件數量。對于目前正在考慮的高斯逼近，這些重要的根值或極點位置顯然是通過選擇公式(6)的適當數量的項(前項)并將它們設為零，然后求解得到的個根。濾波器網絡函數是的有理函數，而不是；因此，在網絡綜合過程中使用，需要將上述得到的根乘以。上述步驟的結果詳見表1，其中包括了高達9階的高斯逼近。在每種情況下，所得到的極點位置已經重新歸一化到頻響的3dB截止點，由于只有個左半平面極點用于網絡綜合，所以只顯示帶負號的實根。

3.1 使用單調諧中間級的參差調諧放大器設計

如果通過設計使用單調諧中間級的梯形調諧中頻放大器來滿足指標是可行的，那么表1的數據就構成了放大器中間級的完整設計數據。

例如，如果要制作一個5級參差調諧放大器，以實現5階高斯逼近，那么需要：兩個單調諧電路，各自的3dB帶寬為所需的總3dB帶寬的倍；這兩個電路將從所需的中頻失諧，頻率間隔等于所需的總3dB帶寬的一半。然后需要兩個單調諧中間級，其各自的3dB帶寬等于所需的總3dB帶寬的倍；這兩個電路將從所需的中頻失諧，頻率間隔等于所需的總3dB帶寬的倍的一半。最后，需要一個單調諧中間級，其3dB帶寬為所需的總3dB帶寬的倍；此電路不會從中頻失諧(detuned)。

放大器所需的總增益可以在5個級之間按任意期望的分布來分配。

3.2 實現高斯幅度逼近的雙調諧級聯放大器

如果通過使用低階中間級和電子管分隔的系統來滿足選擇性要求，那么對于給定數量的放大器級聯，可以通過使用雙調諧中間級來實現比3.1節中的更高階逼近。表1中的極點位置數據也可直接用于設計這樣的雙調諧中間級。對于同步調諧的情況，作者強烈推薦(因為輕微失諧的影響要小于的情況)所需的值可以直接從這樣一個事實中得到：的值必須等于由雙調諧電路提供的極點對的實部。所需的耦合系數可直接從值等于這一極點對的虛部這一事實中得到。上述表達式中的是整個放大器所期望的總3dB帶寬。

表 1高斯幅度逼近的個左半平面根

4. 多元件高斯濾波器網絡

當簡單的(單極點和雙極點)間隔網絡無法用于構建所需的相對衰減形狀并且需要一個單一的集總濾波器單元時，仍然必須使用第3節給出的極點位置進行必要的綜合過程，但知道這些極點位置只是過程的第一步。在進行其他步驟之前，展示一些可以直接應用所得設計信息的實際網絡將會很有幫助。

4.1 低通梯形網絡

圖3顯示了眾所周知的基本低通梯形網絡，可以設計為高斯響應逼近。通過應用基爾霍夫定律，為這樣一個網絡的個元件計算傳輸函數，讀者會發現這個網絡可以描述為：(A)耦合系數-給出相鄰電抗之間的關系；(B)描述與每個單獨電抗相關的電阻損耗的值。值得注意的是，端點處的電抗的值不僅包括它們自身的內部損耗，而且更重要的是，還包括連接到這些端部元件的源或負載的電阻。這些和關系在圖3中詳細說明。需要注意的是，通過將歸一化值(小和倒數)乘以歸一化帶寬變量，可以得到所需的實際耦合系數[例如，]和衰減斜率(或)。

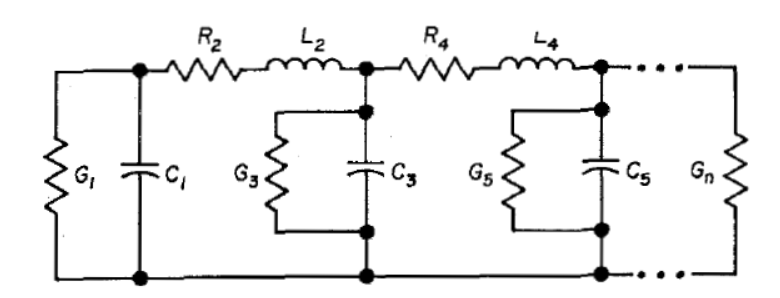
圖3A - 對于以并聯電容器開始的梯形網絡，3dB帶寬歸一化和與 '，，和 之間的關系是：，，依此類推。；依此類推。

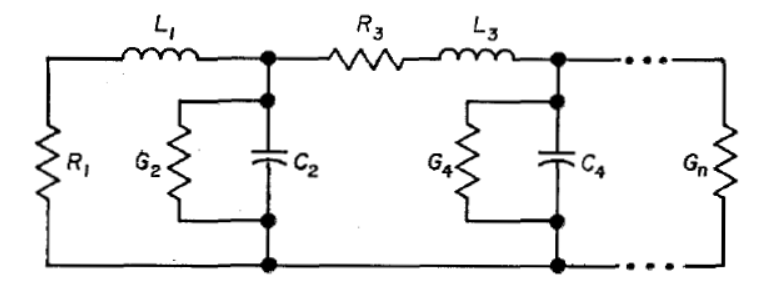
圖3B - 對于以串聯電感器開始的梯形網絡，3dB截止歸一化 '和 與，，和 之間的關系是：，，依此類推。，依此類推。

圖3 - 本文設計數據可以直接應用到的低通梯形網絡。要設計大百分比帶通網絡，首先使用所需的總3dB帶寬為設計上述低通結構，然后在每個并聯電容器上放置一個諧振電感，并將一個諧振電容與每個串聯電感連接，使得每個產生的諧振電路都調諧到通帶的幾何平均頻率上。

4.2 帶通梯形網絡

圖4顯示了適用于小百分比帶通需求的重要情況的耦合諧振器帶通電路。在這里，應用基爾霍夫定律于網絡并求解得到的傳輸函數，該網絡完全由：(A)相鄰諧振器之間的耦合系數和(B)每個單獨諧振器的值來描述；需要注意到，端點諧振器的值由連接到這些端部元件的源或負載電阻以及這些諧振器的內部損耗決定。這些和關系詳見圖4。通過將歸一化值(小和)乘以歸一化帶寬變量，可以得到所需的實際耦合系數[例如，]和衰減()。

5. 相量相對衰減方程(Phasor Relative-Attenuation Equation)及其僅在一端有阻性負載的網絡應用

5.1 無耗或均勻損耗元件的相量相對衰減方程

給定一個與式(5)形式相同的相對衰減幅度方程，相應的相量方程總是可以寫成以下形式：

對于無耗元件網絡，方括號中多項式的系數是通過將表1中的個左半平面根關聯的個因子相乘而得到的，僅僅是產生最小幅值的帶寬處方括號多項式的幅值。對于高斯相對形狀，多項式的最小幅值出現在低通情況的零頻率處和帶通情況的中心頻率(zero fractional bandwidth)處；因此，對于這些響應形狀，。

當濾波器的每個元件(低通梯形中的電抗和帶通情況下的諧振器)具有相同的有限值時，仍然需要使用形式(7)，但是首先需要通過將每個根的實部幅值減少一個等于每個元件歸一化未加載減值(歸一化未加載的倒數)的量來修改所需相對衰減的個左半平面根。然后，將得到的修改后或“預失真”的根值用于相乘以形式(7)的個因子。對于使用修改后根值的這種情況，應該意識到，得到的方程不是我們所期望的相對衰減幅值形狀的相量；而是與“預失真”幅值形狀對應的相量。

譯注：作者在這里考慮了元件的Q值，也就是元件的寄生電阻R，當需要考慮元件電阻R時，就需要預先從根減去一個R所引起的衰減量，即實部減小一個值。這樣最終得到的表達式就是考慮了Q值的表達式，可以用來綜合有限Q值的濾波器。

5.2 連分數展開過程

現在，可以直接使用(7)中的結果系數來獲得圖3和圖4中梯形網絡所需的和值，其中網絡中使用無窮大值或均勻有限值元件。

連分數展開過程的數學基礎將在第6節給出，方法如下：在下面的(8)中，通過將(7)中的第1、3、5等項作為分子，將第2、4、6等項作為分母來形成分數：

圖4A - 使用并聯諧振電路的節點網絡。每個節點的由給出，其中節點電容(或電感)是在其他所有節點短路時跨越節點的電容或電感。對于所示的三種耦合類型：, 和。任何相鄰的一對諧振器都可以通過所示的三種方法中的任何一種耦合，然后如果有必要的話，可以將等效的T型替換為容性或感性的型。在將所有其他節點短路時，每個節點必須在處諧振。

圖4B - 使用串聯諧振電路的網狀網絡。每個網孔(mesh)的由給出，其中網孔電感(或電容)是與網格串聯的其他所有網格斷開時的電容。對于所示的三種耦合類型，, 和。任何相鄰的一對諧振器都可以通過所示的三種方法中的任何一種耦合；然后，如果有必要的話，可以將等效型替換為容性或感性的T型。每個網孔在其他所有網孔斷開時必須在處諧振。

圖4 - 本文設計數據可以直接應用的小百分比帶通梯形網絡以及3dB截止點歸一化和與、、和之間的關系。對于兩種網絡，和 當為奇數時，這個分數是所需的電抗梯形網絡的短路輸入阻抗，從一端觀察到負載，歸一化為這個負載電阻的值；也就是說，對于為奇數，它是。(通過將短路替換為開路，將阻抗替換為導納，將電阻替換為電導，可以得到的奇數的對偶輸入函數。)

當為偶數時，分數(8)是所需的電抗梯形網絡的歸一化開路輸入阻抗。(同樣，可以使用對偶性來獲得為偶數的對偶輸入函數。)

接下來，將(8)展開為連分數形式，由連分數展開的第一個商給出梯形網絡第一個臂的歸一化阻抗，即靠近負載電阻的那一臂。下一個商給出梯形網絡第二個臂的歸一化導納。第三個商給出第三個梯形臂的阻抗，依此類推；阻抗和導納函數交替出現(這種同樣適用對偶情形)。

上述連分數展開產生的商的數值部分通常被稱為歸一化梯形網絡系數，用字母、、等表示。要從這些值轉換為歸一化衰減和耦合系數形式的電路常數，我們使用以下簡單的關系式：

5.3 單端接載梯形網絡的設計

5.3.1 無耗元件設計數據，

當完成(7)，(8)和(9)所描述的數值計算工作后，可獲得表2中的設計數據，該數據用于生成高斯幅度逼近的無耗元件梯形網絡，最高可達9階。注意表中給出了歸一化端部元件的；這只是歸一化衰減的倒數。此外，必須意識到實際所需的耦合系數和端部衰減是通過將表2中給出的歸一化值乘以歸一化帶寬變量(對于低通濾波器)或(對于帶通濾波器)來獲得的。

表2的最后一列給出了小百分比帶通情況下的梯形網絡的網格-網格之間的增益，其中和是獨立選擇的，電壓控制電流源的梯形一端，輸出電壓出現在梯形的另一端。注意有意思的一點是，對于恒定的端接諧振電容，當高斯逼近的階數提高時，傳輸增益顯著降低。

表 2單端加載的“無耗”梯形的階高斯濾波器設計數據

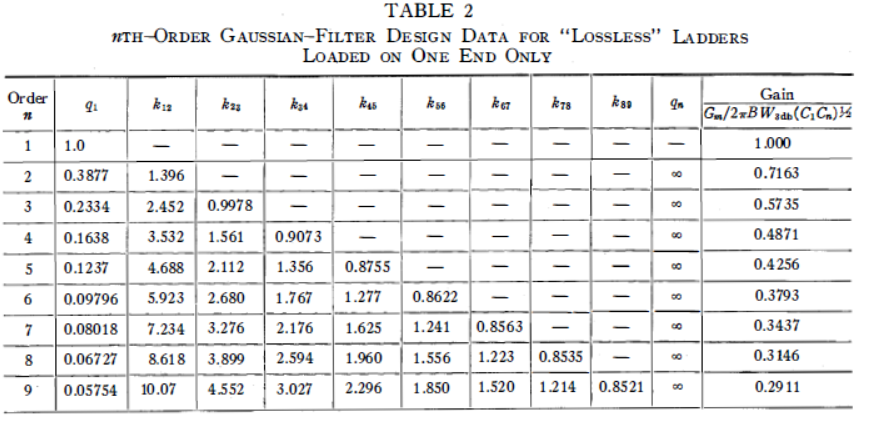
對于低通和大百分比帶通情況，沒有給出零頻率增益列，因為在具有無限元件的情況下，等效戴維南電源的開路電壓將始終出現在輸出端子上。

5.3.2 均勻有耗元件的設計數據， 和

對于由均勻有耗元件組成的5級和8級單端加載網絡，表3和表4分別給出了用于使有耗網絡產生5階和8階高斯逼近所需的歸一化的和。為了節省空間，針對工程師所使用的網絡元件的歸一化無載 的特定值，給出了所需的 和 。顯然，要獲取任何其他歸一化無載 的設計數據，讀者可以通過從這些數據構建圖表來進行插值。

值得注意的是，歸一化無載值較低的元件，如0.7或0.8，可以用于構建實際高斯響應形狀的濾波器。

表3和表4的最后兩列給出了有耗網絡的最大傳輸阻抗()；倒數第二列以一種對于小百分比帶通電路最有用的方式進行歸一化；而最后一列以一種對于低通梯形電路最有用的方式進行歸一化。

在倒數第二列中，對于小百分比帶通情況，給出了格間增益， 和 是第一個和最后一個諧振器的獨立選擇的節點電容， 是源的跨導。

在表3的最后一列(低通增益)， 是并聯在低通梯形網絡中負載電容器上所需的總阻抗。在表4中的相應列中， 是串聯在低通梯形網絡端部電感器上的附加電阻。

確保將源和負載正確連接到在一端或兩端具有并聯元件的梯形網絡的簡單步驟如下：

(A)設計完整梯形網絡，其中需要包括加載電阻，而不需要考慮實際源或負載的具體連接方式和值。

(B)在網絡兩端的電阻上分別畫一個無限阻抗電流源，并在網絡另一端的電阻上畫一個開路輸出電壓端子；在表3和表4的最后兩列中給出的是這個開路輸出電壓與這個無限阻抗輸入電流的比值。

(C)實際要使用的等效電流源幾乎總是會有一些并聯電阻和并聯電容與它相關聯：因此，將輸入節點的并聯 和 分成兩部分，一部分等于必須由要使用的源提供的部分，剩下的部分由電路設計者提供。在網絡負載端采用類似的方法，找到電路設計者必須提供的最后一個節點或網格的那部分。

表 3僅在一端加載的均勻耗散梯形網絡的5階高斯濾波器的設計數據

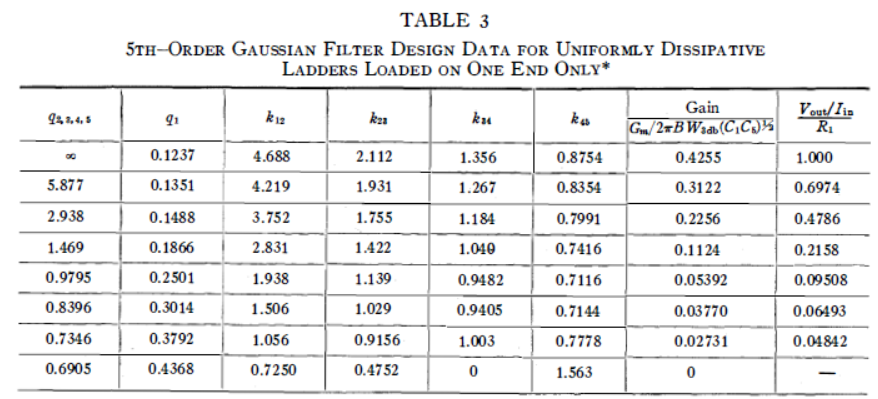
為了節省空間，這個設計信息是針對特定的歸一化無載 值給出的。要獲得任何歸一化無載 的設計數據，讀者應該根據這些數據為 和每個 與 繪制一張圖。

6. 反射系數及其在雙端加載網絡設計中的應用

在達林頓(Darlington)1935年的經典論文 中，他提出了一種用于綜合兩端阻性加載的無源網絡的基本方法(實際上，這種通用的達林頓綜合方法的一個極限情況是在第5節中為單端加載網絡給出的基礎)。下面給出了描述達林頓綜合方法基本原理。

一個基本事實是，如果我們知道純無源梯形網絡在電阻終端處所需的相量電壓或電流反射系數方程，那么可以從這個方程中得到該相同網絡短路(或開路)輸入阻抗(或導納)的更簡單表達式。然后，如果沒有無限衰減的有限頻率點，那么通過對這個輸入阻抗進行簡單的連分數展開，將依次給出滿足原始指定的相量反射系數的梯形網絡的每個無源臂所需的元件值。

有了上述工具，要綜合產生高斯幅度逼近的網絡，需要解決的問題是：如何從所需的相對衰減幅度的形狀開始，從中得到一個終端無源網絡的相應相量的反射系數？

6.1 反射系數幅度的計算

由于指定了一個純無源終端網絡，這個問題非常簡單——所有通過網絡輸入端接收的功率都必須出現在負載電阻上，這樣才能產生所需的相對衰減形狀；因此可以使用下面三個量之間的已知關系：來自電阻源的可用功率 、復輸入阻抗接收的功率以及這個電阻源和這個復輸入阻抗之間的反射系數的幅度平方；即，

對(10)進行簡單的操作，得到重要的形式，

其中 是在接受峰值功率頻率下網絡接收的功率。

表 4僅在一端加載的均勻耗散梯形網絡的8階高斯濾波器設計數據

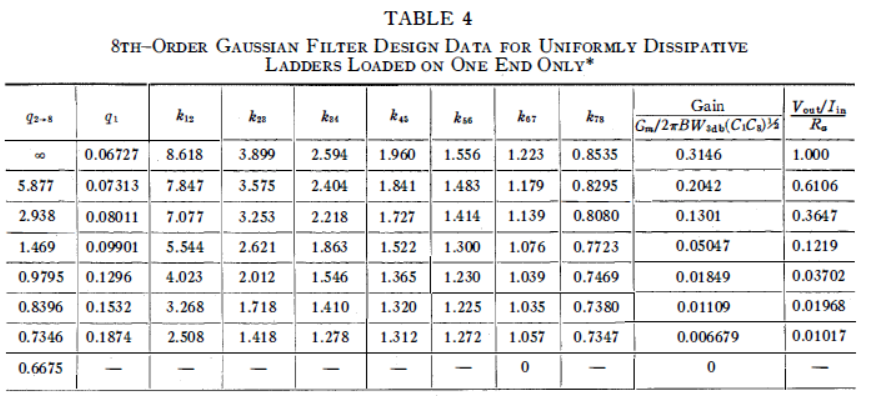
為了節省空間，這個設計信息是針對特定的歸一化無載 值給出的。要獲得任何歸一化無載 的設計數據，讀者應該根據這些數據為 和每個 與 繪制一張圖。

由于在任何頻率下接收的功率 和在峰值頻率下接收的功率 都傳遞給完全相同的負載電阻，它們的比值當然也等于，這是我們所需的相對衰減形狀的幅度平方的方程。由于指定了所需的幅度形狀，因此，(10A)中的方程 是已知的。

(10A)中的量 是在峰值響應頻率下接受的功率與電阻源可提供的最大功率之間的比值，因此是必須選擇的一個簡單比例；可以使用從1到0的任何值。通常，對于在兩端阻性加載的網絡，希望峰值頻率的輸出等于源可提供的最大功率，因此將 設置為1。對于僅在一端電阻性加載的網絡，負載不傳遞功率；在這里， 設置為零。(第5節已經討論了這種情況。)

以上解釋了從指定的高斯逼近相對衰減形狀方程(6)到純無源電阻終端網絡必須具有的電壓或電流反射系數的幅度平方的轉換。重寫(10A)的形式，突出(5)中在分子中的重要作用。通過將(5)的形式作為(10A)的分母，可以得到：

6.2 相量反射系數的確定

接下來的問題是確定與幅度相關的相量反射系數。我們可以分別考慮的分子和分母相量。

首先考慮的分母，需要解決分母的 根(共有 個)，它們必須乘以，然后，因為這個分母是(5)中的多項式部分，即物理可實現的傳輸函數，所以需要選擇 個左半平面 的根，將它們組成的 個根因子相乘得到相量分母。對于理想 元件，這些分母根當然是表1中已給出的那些；對于均勻耗散的網絡元件，這些分母根是通過將表1中根的實部幅度減小每一個元件的歸一化衰減量而形成的預失真根。

接下來考慮的分子；這個方程表明，首先要形成已經得到的預失真相量分母多項式的幅度，然后找到這個方程多項式部分的最小值，然后從這個多項式中減去乘積。現在可以找到這個新多項式的 根。然后將這些根乘以，并選擇得到的 根中的 個，組成所需的 個根因子。這里出現了一個小問題——因為這個分子不是一個物理傳輸或輸入函數，所以這 個根可以有多種選擇方式，但始終要記住，從這些根形成的相量必須具有原始分子的幅度。在本文中，首先選擇所有 個右半平面根，形成一個與(10B)的分子相對應的相量。

當上述根因子相乘時，現在可以寫出與相對應的相量反射系數，

其中， 和 是分母和分子的 個根因子相乘時得到的數值系數。

6.2.1 確定短路或開路輸入阻抗

從上述相量電壓或電流反射系數，可以立即得到相應的終端歸一化輸入阻抗或導納；它是(11)的分母與分子之比與分母減分子之比。

與相應的短路或開路導納相比，這種終端輸入阻抗的展開相當繁瑣，因此直接從(11)中導出后者函數是非常可取的——這是通過在終止輸入阻抗的分子中省略第2、4、6、...項，分母中省略第1、3、5、...項來實現的；得到的結果是(12)，可以直接從(11)中得到。

當 是奇數時，這個比值是所需的無耗梯形網絡的短路輸入阻抗，從梯形網絡的一端看，歸一化到將在這一端使用的加載電阻 的值；也就是說，對于 是奇數，(12) 是。(將短路換成開路，阻抗換成導納，電阻換成電導，就可以得到 為奇數的對偶輸入函數。)

當 是偶數時，(12) 是所需的無耗梯形網絡的歸一化開路輸入阻抗。(再次使用對偶性質可以獲得 是偶數的對偶輸入函數。)

接下來，將(12)以連分數形式展開，連分數展開的第一個商給出第一個梯形臂的無耗部分必須具有的歸一化阻抗(靠近 加載電阻的臂)；接下來的商給出梯形網絡第二個臂的無耗部分的歸一化導納；第三個商給出第三個梯形臂的無耗阻抗，等等；阻抗和導納函數交替出現。(再次使用對偶性質。)

上述連分數展開產生的商的數值部分通常稱為歸一化梯形網絡系數，我們將其表示為, ...。為了將這些 轉換為電路常數的歸一化衰減量和耦合系數形式，使用(13)中的簡單關系。

6.3 確定網絡另一端的短路(開路)輸入阻抗

在上述過程中，實際上已經通過短路或開路梯形來移除了遠端加載電阻；因此，有必要使用額外的步驟來確定所需的加載。推薦的做法如下：為了獲得相量反射系數(11)的分子，從(10B)的分子根中選擇了個根，它們成對共軛。現在，如果使用關于 軸的另外 個鏡像根來形成(11)的分子，那么在觀察網絡另一端時，將得到所需的相量反射系數，歸一化到必須在這另一端使用的加載電阻。

表 5兩端阻性負載的階零功耗高斯濾波器設計數據，無耗元件梯形網絡

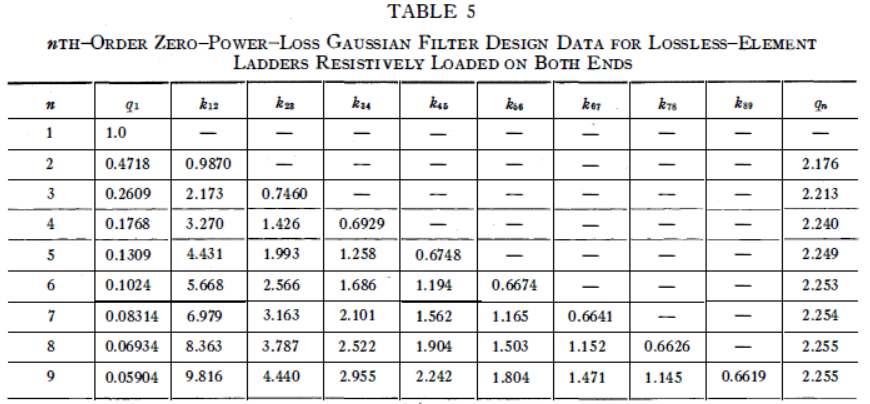
兩組根產生的數值系數相同，但是，對于鏡像根，(11)分子中的第2、4、6、...項的符號將與原始根集合獲得的符號相反。

因此，當形成該網絡另一端的短路(開路)輸入阻抗(導納)函數時，它將完全以(12)的形式呈現，但分母項將由指示的 U 和 之差而不是和組成。

將這個新函數以連分數形式展開，將給出歸一化到網絡遠端的終止電阻的梯形網絡臂阻抗。連分數展開的商的數值部分給出了一組新的梯形網絡系數，并從以下公式中獲得元件衰減量和耦合系數：

需要的最后一個臂的加載衰減量 是所需的信息，作為數值工作的檢查，(14)中的相應歸一化 應該與(13)中的相同。應該記住， 是每個網絡元件的歸一化均勻未加載衰減量；也就是說，對于低通無耗阻抗， 和，對于要使用的帶通諧振器，。

6.4 雙端接載最大功率傳輸梯形網絡的數值設計數據

6.4.1 無耗元件設計數據

當完成(10B)、(11)、(12)、(13)和(14)所概述的數值工作后，我們可以得到表5中的設計數據，該數據用于產生高斯幅值逼近的無耗元件梯形網絡，直至第9階。

與本文中呈現的所有設計數據一樣，這些是3dB帶寬歸一化值。對于帶通情況，實際所需的是通過將 值乘以所需的 的倒數來獲得的，實際所需的 是通過將 值乘以所需的 來獲得的。對于低通情況，歸一化帶寬變量是。

這些設計都具有零中頻功率損失；在通帶的中頻，所有來自等效電阻和源的可用功率都傳遞到電阻負載。根據這個事實，帶通和低通傳輸阻抗或增益可以簡單地計算出來。

在實踐中，表5中的無耗元件設計數據主要適用于低通和大百分比帶通濾波器，因為這些情況下對無限歸一化空載 的假設基本上是滿足的。(請記住，低通梯形網絡中電感器的歸一化空載 是)。

表 6均勻耗散梯形網絡電阻式兩端加載的5階最小功率損失高斯濾波器設計數據*

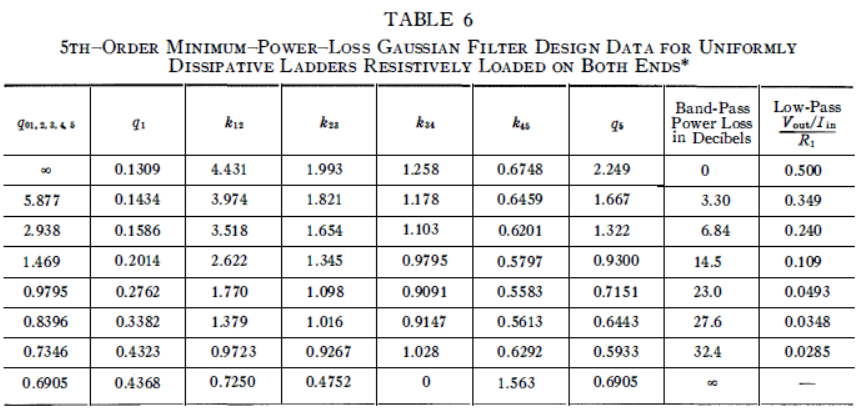
為節省空間，這些設計信息針對特定值的歸一化空載進行呈現。要獲取任何歸一化空載的設計數據，讀者應根據這些數據繪制和每個與的圖表。

表 7均勻耗散梯形網絡電阻式兩端加載的8階最小功率損失高斯濾波器設計數據*

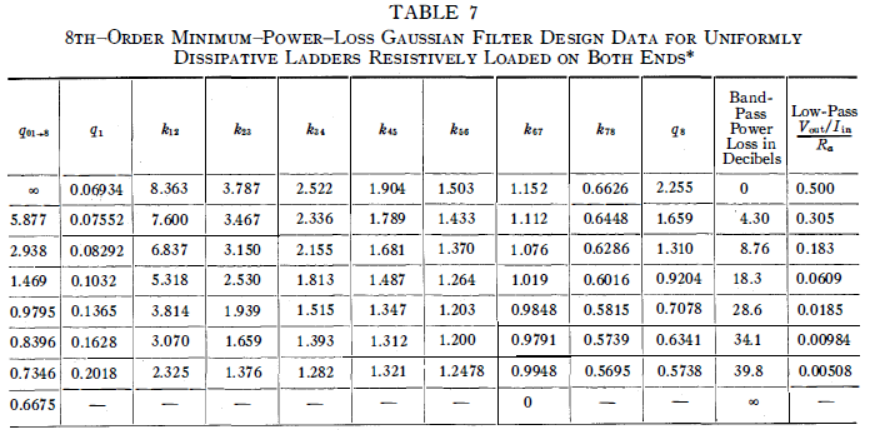
為節省空間，此設計信息僅針對特定的歸一化無載Q值提供。要獲取任何歸一化無載Q值的設計數據，讀者應根據這些數據繪制一張和每個與之間的圖表。

6.4.2 均勻損耗元件設計數據 和

在小百分比帶通電路中，歸一化無載諧振器 是一個重要的參數，其定義為。在實際應用中，這個 很少大于10，甚至在某些情況下可能低至2或3。這意味著在這種情況下，我們不能假設電路元件具有無限無載值。

為了解決這個問題，我們可以對表1中的高斯逼近根位置進行預失真處理，即將其除以。然后，按照第6節中的綜合過程進行設計。這樣，我們可以得到表6中的5階有損高斯梯形設計數據和表7中的8階有損高斯梯形網絡設計數據。這些高斯梯形電路在源阻抗和電阻負載之間工作，能夠在給定無載元件的情況下，實現最小的中頻功率損耗。

在這些表格中，最后一列給出的增益信息類型與表3和4中詳細描述的相同。簡而言之，這些增益信息可以幫助我們了解在不同設計條件下，電路的性能如何受到影響。通過對這些數據的分析，我們可以優化電路設計，從而在實際應用中實現更好的性能。

7. 設計實例

7.1 低通濾波器實例

7.1.1 要求：一個5階低通高斯濾波器，3dB帶寬為1.32MHz。

7.1.2 使用在3dB截止頻率處測量的無載Q值為100的電感在經濟和結構上是可行的；當然，這就是低通歸一化無載元件Q，即。從表3或表6的第一列(讀者可以根據這些表格準備的圖表的橫坐標)可以看出，Q值為100將導致一組所需的k值和末端q值與無限無載Q集合可以忽略不計的差異。[準確的所需值可以從準備好的圖(圖5)中讀取，但對于這個例子，我們將使用無限無載Q集合。]

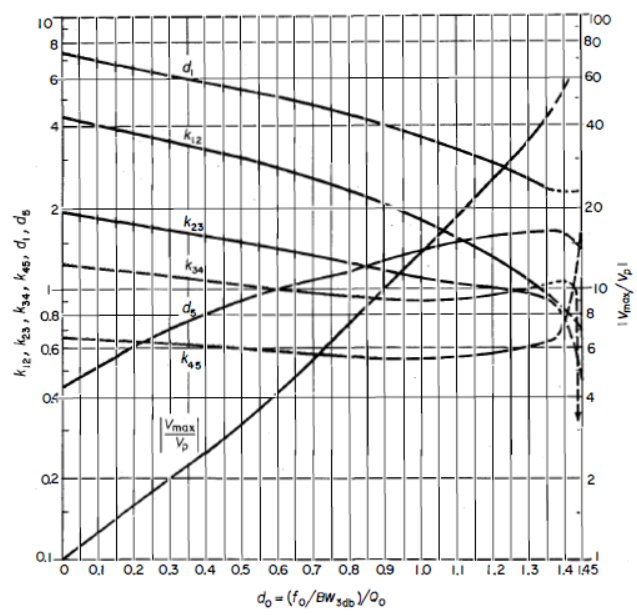
圖5-最低損耗(Minimum-transducer-loss)3dB截止歸一化和，需要產生高斯逼近幅度形狀。 和。

7.1.3 單端加載的濾波器在正確調整單個負載電阻和k值方面對其正常運行的依賴程度要高于雙端加載的網絡。因此，決定使用雙端加載設計；將使用表6。

7.1.4 為了吸收與等效源相關的分布電容，將使用其第一個元件為對地電容的低通梯形。

譯注：簡單來說，我們使用這種具有并聯電容作為第一個元件的低通梯形電路來優化電路設計，使其能夠在降低與源等效相關的并聯電容影響的同時，保持濾波器的性能。

7.1.5 值得注意的是，如果源等效和負載電阻是由諸如電子管或晶體管之類的有源元件產生的，那么在整個源信號周期內確保它們的動態阻抗保持真正恒定的值非常重要。在不使用顯著負反饋的情況下，這很難實現，通常情況下，在信號周期的低電流部分，動態阻抗明顯高于高電流部分。最安全的做法是將潛在的非線性源和負載與網絡的末端隔離，并使用真正的電阻來提供源和負載電阻。

簡而言之，如果我們使用像電子管或晶體管這樣的有源組件產生等效源和負載電阻，那么就需要確保在整個驅動信號周期內，這些組件的動態阻抗保持恒定。如果不采取適當的措施，如在有源元件周圍應用負反饋，這將難以實現。在信號周期的低電流部分，動態阻抗通常會比高電流部分更高，從而影響電路性能。

為了避免這種問題，最好的做法是將具有非線性特性的發生器和負載與網絡隔離，并使用真正的電阻器件來提供發生器和負載電阻。這樣可以確保電路在整個信號周期內保持穩定的性能，從而提高整體系統的效率和準確性。

7.1.6 在要插入濾波器的系統中，信號幅度和增益考慮要求整體低通濾波器的傳輸阻抗至少為75Ω。從表6的低通傳輸阻抗列可知，這要求(上的結果負載電阻)為150Ω。

7.1.7 現在通過從開始，逐個元件向右進行低通設計。

(A) 對于第一個元件為對地電容的低通梯形網絡，

Therefore,

Therefore,

is of course the 3 -decibel-down radian frequency of the combination by itself ; thus the 3-decibel-down frequency of this combination must equal 10.1 megacycles. 當然是組合本身的3dB截止弧度頻率；因此，這個組合的3dB截止頻率必須等于10.1MHz。

在完成的濾波器中，檢驗和是否正確的一個好方法是實驗測量這個組合的3dB截止頻率。

圖6 - 低通高斯逼近濾波器的實際尺寸示意圖，該濾波器是根據第7.1節的低通設計示例綜合的。

(B) 對于這個低通梯形網絡，

因此,

得到,

當然是組合本身的諧振頻率；因此，必須與已知的在5.85MHz處諧振。

在完成的濾波器中，確定正確的最佳方法是實驗測量和的諧振頻率。

(C) 要獲得第三個低通元件值，

因此，必須與在2.64MHz處諧振；

(D) 和 (E) 依次應用和列得到所需的相鄰臂諧振頻率和元件值，即MHz；uH，MHz；pF。

(F) 最后，列給出了組合本身所需的3dB截止頻率

現在低通濾波器的設計已經完成。圖6是一個實際濾波器的照片。

這種濾波器的實驗觀測性能值得關注，圖7是一個復合圖像，顯示了類似于上述設計單元的濾波器的一些響應特性，但其3dB帶寬為0.84MHz。

7.2 帶通濾波器設計示例

7.2.1 需求：一個用于載波中心雙邊帶系統的5階帶通高斯濾波器。所需中頻為70MHz，所需的3dB帶寬為2.75MHz。因此，所有與衰減量和耦合系數相關的參數需要被歸一化處理，歸一化的基準是3dB帶寬與帶寬之比，其值為。

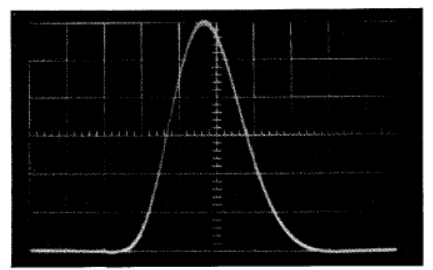
圖7A - 濾波器的3dB帶寬為0.840MHz，掃描速度為us/cm。驅動為0.18us脈沖源。

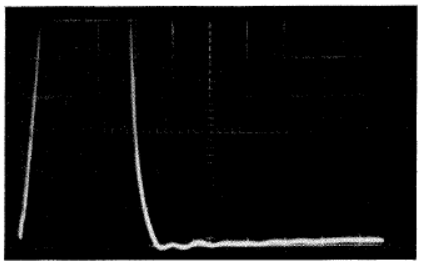
圖7B - 與圖7A相同的脈沖輸出，但示波器增益增加了，使得一個垂直檔位為峰值脈沖輸出的；顯示的下沖和振鈴約為峰值輸出的60dB以下。

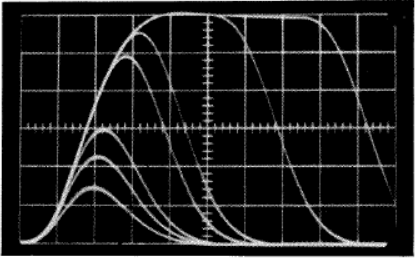
圖7C - 濾波器輸出作為脈沖輸入寬度(恒定輸入幅度)的函數。輸入脈沖寬度分別為和0.10us。掃描速度為us/cm。

7.2.2 在70MHz的頻率下，使用具有150至200區間的無載Q值的商用鐵氧體磁芯調諧線圈作為諧振器是實際和經濟的。將要使用的鍍銀云母電容器具有約1000的Q值。因此，諧振器的無載Q值將在130至170的范圍內。為了獲得實際的諧振器無載Q值，重要的是將實際的電感和電容放置在將在濾波器實體中使用的屏蔽隔室中，然后使用與屏蔽諧振器非常松散耦合的源和檢測器測量其無載3dB帶寬。如果測量的無載諧振器Q值為150，那么歸一化的無載Q值將為。因此，表3和6中的第二行給出的設計數據可以直接使用。如前所述，可以通過繪制表格的適當區域來獲得任何可用諧振器無載Q值的k值和末端元素q值。

7.2.3 濾波器將在五極管(pentode tube)之間工作，因此可以使用僅在一端加載的設計；然而，由于使用雙端加載設計時，響應形狀對元件值變化的敏感性較低，因此將采用后者來進行設計。

7.2.4 在驅動電子管的柵極和陰極之間放置一個75Ω的電阻，因為柵極對電子管的偏置電壓變化和老化所致的傳輸時間和空間電荷輸入阻抗變化較大。如果要在較小的公差范圍內復現響應形狀，那么最好不要在這個柵極到陰極阻抗中使用濾波器諧振器。還決定在柵極和陰極之間使用一個電感器來抵消該端口的輸入電容(約13pF)。由于它的帶寬非常寬，所以在濾波器的整個帶寬范圍內，它可以被認為是一個純75Ω的電阻終端，用于連接濾波器本身到柵極的75Ω電纜。由于它有適當的終端匹配，所以這個電纜的長度并不關鍵。

7.2.5 對于多諧振電路濾波器，實用的校準方法與正確的設計同樣重要——文獻中提供了一種推薦的校準方法。當濾波器的低Q端連接到源時，此過程中使用的交替最大值和最小值更容易觀察。在表6中，諧振器1位于濾波器的低Q端；因此，出于校準的原因，這一端將由源驅動，75Ω負載將轉換為濾波器的高Q端(第五個)諧振器(轉換過程將在后面討論)。

7.2.6 系統要求管子和濾波器電路提供的柵-柵電壓增益至少為1。簡單地計算負載功率與可用源功率的方程，可得結果為

其中為等效源電阻，比值為功率增益(小于1)，以dB為單位給出在表5、6和7的功率損耗列。對于歸一化的無載Q值為5.88，表6顯示中頻功率損耗為3.3dB或。如果電子管驅動具有12000uΩ的，(15)表明源阻抗必須為820Ω才能使得柵-柵增益為1。

7.2.7 出于兩個原因，決定將濾波器的第一個諧振器直接放置在驅動管的陽極中。

(A) 820Ω的源電阻與管子和接線輸出電容(約4pF或570Ω的電抗)并聯。因此，當諧振時，等效源將具有1.44的Q值，或歸一化Q值為0.056。從表6可知，諧振器1的歸一化加載Q值必須為0.1309；源歸一化Q值顯然不是與此值相比為零，因此不能認為源是純阻性的，并試圖通過阻抗變換將其耦合到這個端諧振器。

(B) 即使它是一個純阻性源，可能也無法構造出一個作為單獨實體的變壓器，該變壓器具有可忽略的頻率響應；也就是說，與此端接諧振器所需的低加載Q值相比，歸一化Q值可忽略不計。

7.2.8 在小百分比帶寬濾波器中，內部諧振器的電感(或電容)的中頻電抗可以獨立于響應頻率要求或增益要求來選擇——可以根據獲得最大無載諧振器Q值和實用機械結構的要求來選擇電抗值。

對于這些內部諧振器，將使用85Ω的電抗，需要27pF的總節點電容。

對于小百分比帶寬濾波器的端部諧振器，有如下需要注意的地方：

(A)如果要將電阻性源或負載通過阻抗變換來正確設置第一個和/或最后一個諧振器，則這里的諧振器電抗也可以根據實用的機械結構和高無載Q值來選擇。

由于要將歐姆電阻負載轉換為正確的第五諧振器，這個端部諧振器可以類似于內部諧振器；一個需要27pF總諧振電容的電感器。

(B)然而，如果源或負載要直接連接到第一個或最后一個諧振器，則源電阻與諧振器電抗之間的比值必須恰好滿足表6中(或)列的要求；如果源電阻固定，則必須使用特定的諧振器電抗，反之亦然。

在本例中，源電阻已固定為820Ω，并且將直接放置在第一個諧振器上。注意到，其中是將源電阻單獨放置在諧振器上產生的歸一化衰減值，(16)可以簡單地導出，并給出諧振器電抗與源電阻之間所需的關系。

其中是表6中列的倒數，是列的倒數。

將值代入(16)可得，或pF。

7.2.9 現在每個節點的總電容已經確定，需要決定要在相鄰節點之間使用的耦合機制。關于耦合機制選擇的堅定規則很難制定-一般來說，由機械結構支配的設計者的獨創性可以導致多種選擇。我們將在第一個節點和第二個節點之間使用電容耦合，在第二個節點和第三個節點之間使用電容耦合和輔助互感耦合的組合，在第三個節點和第四個節點之間使用電容耦合，在第四個節點和第五個節點之間使用互感耦合，以及通過高側電容阻抗轉換來正確地用75歐姆電阻負載加載第五個諧振器。

7.2.10 使用表6第二行的設計數據，現在可以設計濾波器網絡。

在下面的步驟中，計算將給出所需耦合系數所需的耦合電容或互感。然而，必須指出的是，由于用于濾波器網絡實物中的屏蔽封裝導致接地平面靠近，這會顯著影響電容器提供的直接電容值，甚至更強烈地影響電感器或一對電感器提供的自感或互感值。因此，特別是當需要較小的值時，濾波器中實際所需的耦合電容器和/或電感器通常無法通過表(例如)測量組件直接獲得；文獻中詳細介紹了一種實驗性設置每個耦合系數和每個端部的推薦方法。由于所述方法在濾波器組件將在最終實物中占據的確切位置下測量兩個明確定義的響應峰之間的帶寬，因此實際上可以將每個系數設置為所需值的1%以內。一旦獲得了正確的值，可以使用表或直接測量物理尺寸來復制這些正確的值。

(A) 所需的是

我們已經通過在步驟7.2.8中使用(16)滿足了這個要求。

(B) 第一節點和第二節點之間所需的耦合系數是

因此，所需的高側耦合電容為

(C) 第二節點和第三節點之間所需的耦合系數是

在電感器盡可能靠近的機械布局下，測量得到的互感耦合系數為0.0344(此通過峰值帶寬方法測量)。因此，所需的電容耦合為

因此，所需的高側耦合電容為

(D) 第三節點和第四節點之間所需的耦合系數是

由于只使用高側電容耦合，

(E) 第四節點和第五節點之間所需的耦合系數是

由于這個系數是由互感耦合提供的，所以峰值帶寬測量是設置電感4和5之間物理間距以獲得此值的推薦方法。

因為這個特定的系數對整個濾波器的3dB帶寬度有重大影響，設計師可能希望使電感器編號5的位置略微可調，以便生產線上的調整可以用來精確設置濾波器的3dB帶寬。

(F) 最后，必須設置加載的端部諧振器。從表6中，

這個是由第五個諧振器的空載和75Ω負載的變換阻抗效應所共同決定的。對這個關系進行簡單處理，得到(17)式所需的變換阻抗：

將當前值代入(17)得到所需的變換阻抗 5030Ω。這里所需的大阻抗變換可以通過在75Ω負載和第五個諧振器頂部之間連接一個高側電容器來簡單地實現，其電抗為

因此

使用這種簡單的變換方法，傳遞給負載的電壓相對于頻率略微不對稱，高頻響應的下降速度不如低頻響應——對于小百分比帶寬，通常可以忽略所產生的不對稱性。

圖-直接綜合的節點網絡。

圖-第7.2節描述的精確等效網絡使得在電路中加入一段同軸電纜成為可能。

圖8-70MHz中頻5階帶通高斯逼近濾波器的原理圖，該濾波器在第7.2節的帶通設計實例中綜合。電容以pF為單位，電阻以Ω為單位。未標記的電阻表示空載諧振器的等效損耗。給出的元件值僅顯示兩位有效數字，而耦合系數公差通常要求2-5%的精度。這樣做是為了強調在沒有在濾波器中占據的確切物理位置的情況下，通常無法通過對組件的測量來精確調整這些耦合系數。相反，這些必須通過等效于峰值帶寬測量過程的方法來設置。類似地，必須發展類似于例如描述的充分校準方法，并在本文的圖10中加以說明。

圖9-第7.2節帶通設計實例中綜合的70MHz帶通5階高斯逼近濾波器的實現。此濾波器的第一個諧振器包含在另一個單元中。

圖是所得濾波器的示意圖。

7.2.11 為了制造的目的，希望濾波器是一個獨立的無源實體。通過在濾波器負載端使用75Ω電纜連接器，可以將此端與設備的其余部分物理分離(參見第7.2.4節)。然而，由于濾波器的第一個諧振器直接連接到驅動管的陽極，顯然不可能將濾波器的這一端與設備的其余部分物理分離。如果希望將最后四個諧振器作為一個單獨的單元，通過電纜連接到包含第一個諧振器的單元，可以使用以下步驟。

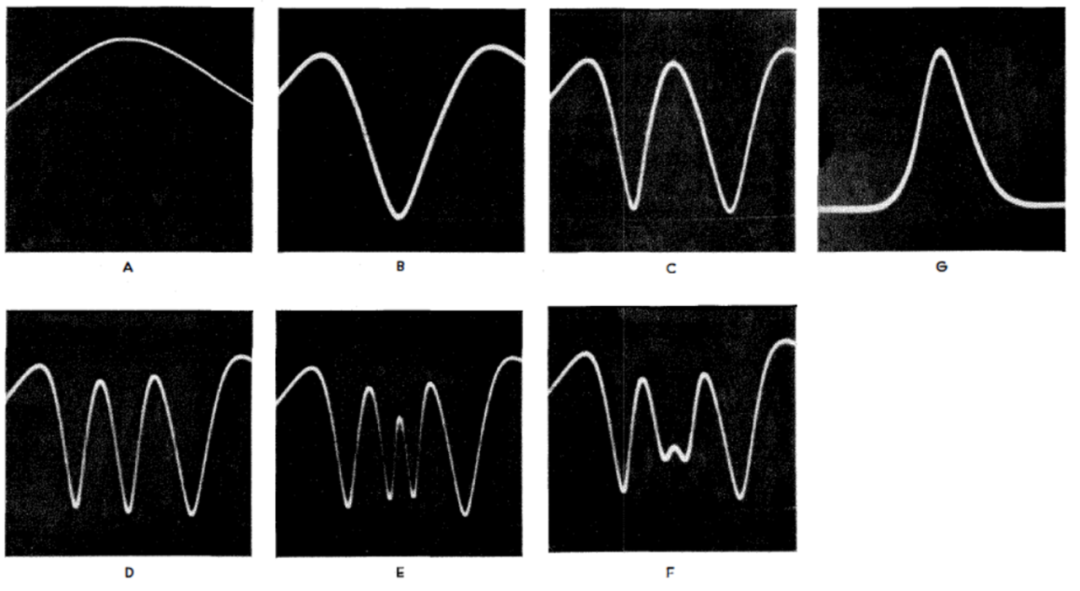
圖10-當將檢測器耦合到第一個諧振器并使用以下校準方法時，在5階高斯逼近濾波器的第一個諧振器上出現的電壓幅度與頻率現象：(A) 第二個諧振器被短路，第一個諧振器在期望的中頻(70MHz)調諧為最大電壓。(B) 第三個諧振器被短路，第二個在期望的中頻調諧為最小電壓。(C) 第四個諧振器被短路，第三個調諧為最大中頻電壓。(D) 第五個諧振器被短路，第四個調諧為最小中頻電壓。(E) 最終負載被短路，第五個諧振器調諧為最大中頻電壓。(F) 最終負載被正確地轉換成第五個諧振器，然后重新調諧為最大中頻電壓。(G) 得到的5階高斯逼近傳輸形狀。

(A) 第一和第二節點的節點到地電容的一部分與總的(2.57pF)結合形成一個容性。

(B) 將此容性轉換為容性T。

(C) 通過一段電纜實現此T的并聯臂，電纜的長度(當然，與波長相比必須非常短)應該足夠提供所需的并聯電容。

圖 顯示了包含這個“耦合系數電纜”的濾波器原理圖。

值得注意的是，820Ω源電阻上留有4pF的電容；這是驅動電子管的輸出電容。因此，已經從變換為T的電容包括3.4pF的并聯腿和2.6pF的高側腿。再次強調，在第7.2.10步中得到的電容值和圖8中僅給出的兩位有效數字僅供參考——耦合系數和端Q值應通過其他地方詳細介紹的程序進行實驗調整和檢查，精度為正負2%。

圖9是一個實例的照片，其中高斯中頻濾波器的最后四個諧振器包含在一個鑄件中。左側進入的電纜提供了圖要求的11pF電容，以滿足，右側的電纜通向75Ω電阻負載。

為了使濾波器能正常工作，每個節點必須精確地調諧到期望的中頻(70MHz)。圖10顯示了當應用推薦的調諧方法時，在第一個諧振器上觀察到的輸出電壓(通過松耦合的檢測器)；最后的照片顯示了正確校準濾波器的傳輸幅度-沒有重新調整調諧控制便獲得了此傳輸圖像。

審核編輯：湯梓紅