上一節中說到，需要求使損失函數最小的權重和偏置，高中數學中，求函數的極值就是使函數導數為0的點。

1、導數

導數是某個瞬間的變化量，瞬間的定義是時間趨近于0

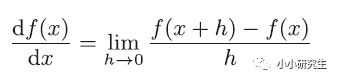
使用代碼來實現：

def numerical_diff(f,x):
  h=10e-50
  return(f(x+h)-f(x))/h

此時，h取一個極小的數來表示趨近于0，但是如果太小的話在計算機中貴產生舍入誤差，用float32的浮點數來表示依然是0.0。另外，上述定義是函數f在x與x+h之間的差分，是近似的導數定義，而真正的導數是曲線在某一點上的切線，這個誤差產生是由于h不可能無限趨近于0。因此，可以計算f在x+h和x-h之間的差分進一步減小誤差。

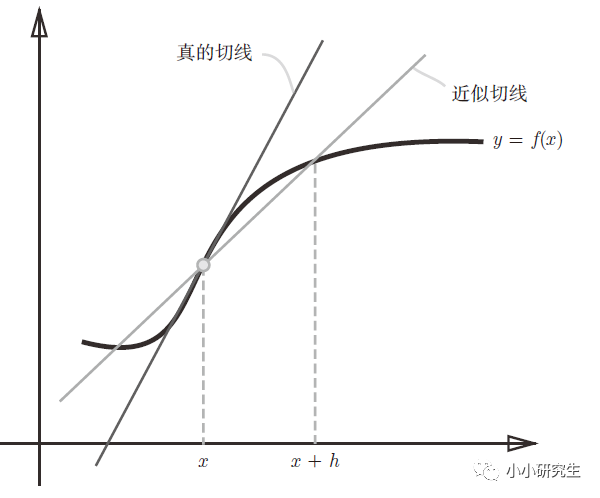
真正數值微分的代碼：

def numerical_diff(f,x):
  h=1e-4
  return (f(x+h)-f(x-h))/(2*h)

真正用函數的導數計算出的結果是解析解，而數值微分近似的結果嚴格意義上并不一致，但是由于誤差可以忽略不計，因此可以認為它們是相等的。

2、偏導數

當函數y有多變量時，多變量函數的導數就是偏導數。求偏導數時，多變量中的一個變量是目標變量，其他變量需要為定值。

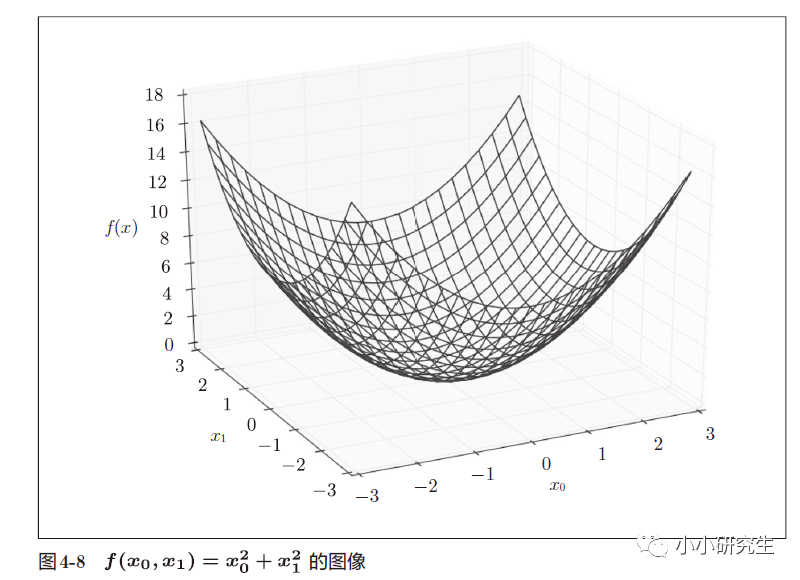
求偏導的代碼：

def function_2(x):
  return x[0]**2+x[1]**2

3、梯度

偏導數匯總而成的向量成為梯度。

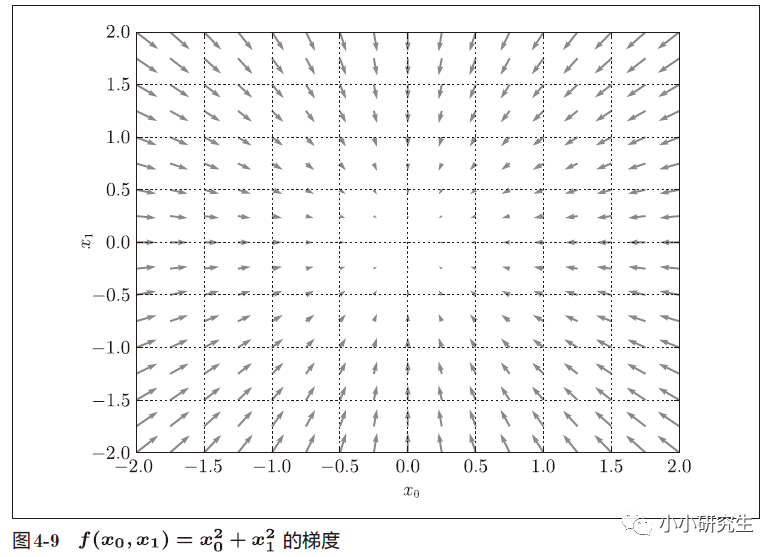
向量是有大小和方向的，在梯度圖中，箭頭的指向就是梯度的方向，箭頭的長度就是梯度的大小。 梯度總是指向函數值減小最多的方向。

知道梯度的定義，就可以用梯度來使損失函數減小。復雜函數中，梯度指示的方向基本上都不是函數值最小處，但沿著梯度方向可以最大限度減小函數的值。在梯度法中，函數的值從當前位置沿著梯度方向前進，然后在新的地方重新求梯度，再沿著新梯度的方向前進，不斷重復，逐漸減小函數值。尋找最小值的梯度法是梯度下降法，尋找最大值的梯度法是梯度上升法，一般神經網絡中梯度法主要是指梯度下降法。

4、梯度法求某個函數值優化結果

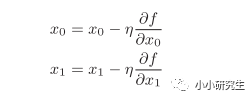
η是學習率，表示更新量，決定在一次學習中，應該學習多少以及在多大程度上更新參數。上式會反復執行，逐漸減小函數值。學習率需要事先確定，過大或過小都不行，一般會一邊改變學習率一邊確定學習是否正確進行。

梯度下降法代碼：

def gradient_descent(f,init_x,lr=0.01,step_num=100);
  x=init_x
  for i in range(step_num):
    grad=numerical_gradient(f,x)
    x-=lr*grad
    return x

參數f是要最優化的函數，init_x是初始值，lr是學習率，step_num是重復次數。 numerical_gradient()會求函數梯度，并更新x。

當使用梯度法求f(x0,x1)=x0^2+x1^2的最小值時，設置初始值為(-3,-4)，學習率為1，上面次數定義的時候是100，實際使用的時候設置是20，最終結果為[-0.03458765 0.04611686]。 使用解析法求最小值是[0,0]，因此結果在一定程度上可以認為是一致的。

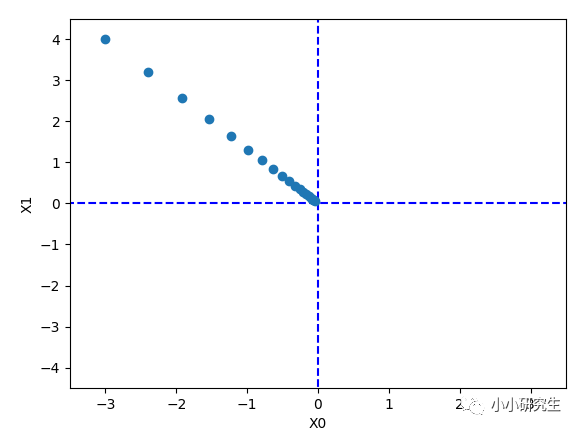
對梯度法每次迭代進行繪圖顯示，函數的取值在向原點(最小值處)逐步靠近。

學習率的設置非常重要，當我們將其設置為10時，結果為[-2.58983747e+13 ，-1.29524862e+12]發散成一個很大的值。 當設置成1e-10時，結果為[-2.99999999 ， 3.99999998]幾乎沒有什么變化。 學習率這種超參數和權重偏置不同，只能人工設定，需要嘗試多個值。

5、梯度法求神經網絡的損失函數優化結果

class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3)
    def predict(self, x):
        return np.dot(x, self.W)
    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)
        return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)

init (self)創建一個隨機的2*3的矩陣，predict(self,x)讓x與W矩陣相乘，loss(self,x,t)定義了損失函數。 給定了x,t之后調用了實例化的類，再將net.loss傳遞給f后，在numerical_gradient()函數中進行調用求梯度。

至此，求出了神經網絡的梯度，接下來只需要根據梯度法更新權重參數。