下圖是我們常見的用于仿真OP的AC特性(DC增益、GBW等)的Bench。我們通過在OP的輸出和輸入之間串聯一個一階RC網絡(R、C值通常都很大)的形式組成一個閉環系統,而我們需要的其實是OP的開環特性。
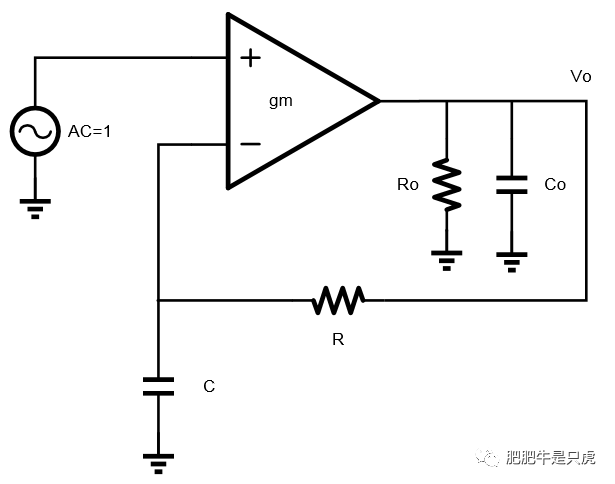
本文試圖弄明白以下幾個問題:
為何通過閉環的方式可以得到OP的開環AC特性?
R、C對仿真結果有什么影響?
R、C要取大,那到底要多大?這個問題和上面的問題關聯度很大。
問題很基礎,過程很重要,答案不簡單。
先推導這個Bench的閉環傳函:
這是一個電壓-電壓負反饋,其閉環系統的傳函可以用標準反饋方程Y/X=G/(1+G*β)來統一。
第一步:先斷環,考慮加載效應,見下圖
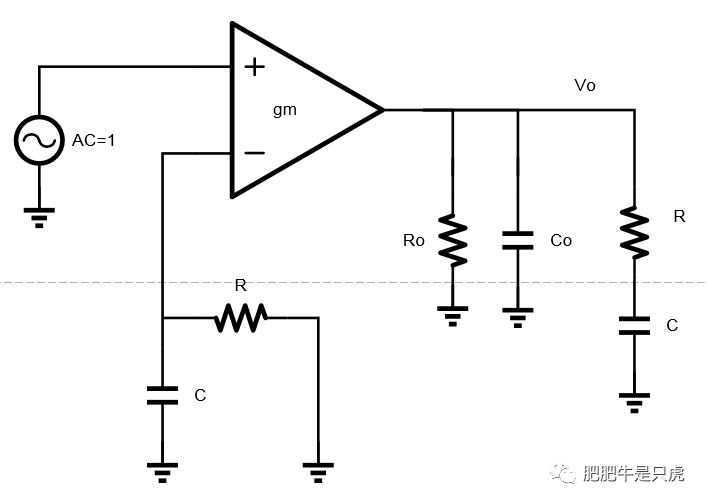
第二步:計算前饋增益G(s),對于VV反饋,其實就是OP的開環增益,如下:
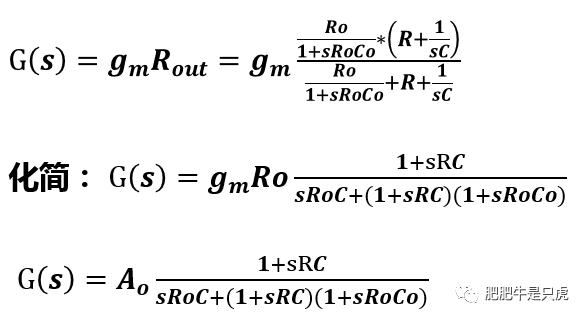
第三步:計算反饋系數β(s)
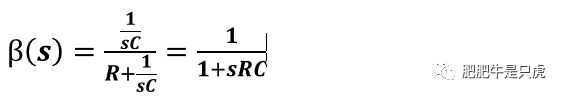
第四步:計算閉環增益A(s),A(s)=G(s)/(1+G(s)*β(s))

至此,我們得到整個系統的閉環傳函,上面的推導過程中僅僅做了如下近似:
RC>>RoC,且RC>>RoCo,
由于R和C都是很大的值,這個近似誤差可以忽略不計。
接下來,該分析閉環傳函了
我們嘗試盯著閉環傳函A(s)的表達式看,能看出點啥?
閉環傳函有一個LHP零點:z=-1/RC
閉環傳函分母是一個標準的二階形式,有2個根,對應著2個LHP極點,
假設分母的兩個極點分別為p1和p2,且|p1|<<|p2|,則
p1+p2=-1/(Ro*Co)≈p2
p1 p2=Ao/(Ro R C Co)
聯合上面兩個式子,不難得到:
p1=-Ao/(R*C)
p2=-1/(Ro*Co)
至此,我們得到了整個閉環系統的零極點分布情況,總結下:
z=-1/(RC)
p1=-Ao/(R*C)
p2=-1/(Ro*Co)
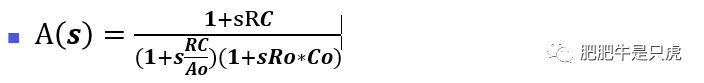
不難看出,p2是OP本身的輸出極點,z和p1的頻率極低,構成一對低頻零極點對。當頻率遠>這一對零極點對之后,A(S)可以簡化為:

繼續盯著這個表達式看,這個表達式什么意思?
這不就是我們想要的OP的開環AC特性嗎?
我們費盡千辛萬苦,終于在這一步得到我們想要的。
畫個圖,可以看得更直觀:
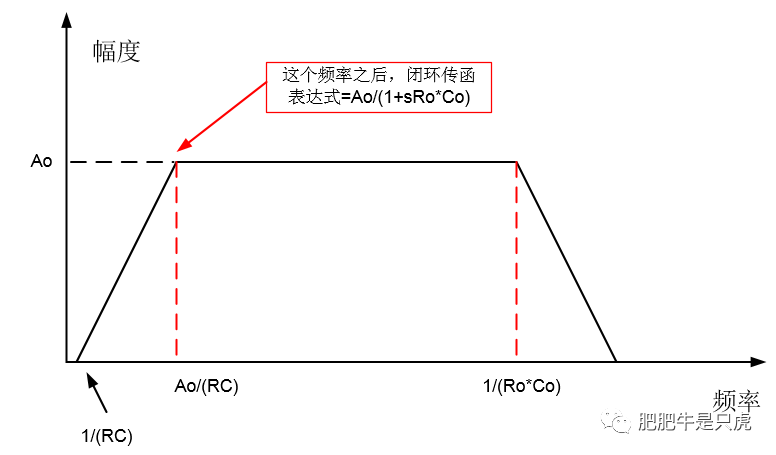
行文到此,問題基本上說清楚了,我們回到文章開頭的幾個問題,這時候應該有答案了吧!
對于RC的取值問題,我們要保證Ao/(RC)<<1/(Ro*Co)即可。
舉個例子:
R1=10^12,
C=1,
OP增益Ao=1000倍(60dB),
則RC造成的低頻極點為1000/(10^12)=10^(-9),是一個極低頻率的值,低到我們可能壓根兒都沒發現它的存在。因為我們在跑AC的時候會給定一段頻率,比如從1Hz~1GHz,也就是說低于1Hz的波形我們壓根兒就沒看,所以我們跑完AC觀看波形的時候會發現AC曲線低頻是平的,并沒有我們文章所講的一對低頻零極點。看官如果想看到這一對零極點,從很低頻的部分開始跑AC即可,或者把RC的取值取小一點兒。
直觀解釋
終于到了群眾喜聞樂見的“直觀解釋”環節了,先把Bench拷貝過來,對照著說。

OP正輸入端AC=1
OP負輸入端AC≈0,為什么呢?因為C很大,阻抗1/(sC)很小,頻率稍微高一點,就近似于短路
R的作用:通直流隔交流,R可以將OP的輸出和負輸入短路,建立直流工作點。但是對于AC而言,大R基本不構成加載效應,不會影響OP增益。
OP正負輸入AC=1,所以直接觀察OP輸出Vo就可以得到OP的增益的開環AC特性。
-
串聯
+關注
關注
6文章
424瀏覽量
37635 -
仿真
+關注
關注
50文章
4111瀏覽量
133786 -
AC
+關注
關注
1文章
588瀏覽量
84413 -
負反饋
+關注
關注
6文章
217瀏覽量
30105 -
閉環系統
+關注
關注
0文章
17瀏覽量
9435
發布評論請先 登錄
相關推薦
用TINA仿真OP07電壓跟隨器遇到的疑問求解
OP放大器的開環頻率特性
OP279在Vs=±5V的電氣特性參數:short current limit只有±50mA如何理解?
應該怎么去理解AC magnitude 這個參數呢?它為什么會影響增益?
對于AC/DC/AC電源以及死區特性的MATLAB建模
用multisim仿真使用OP295反饋電路時,如何使用波特儀測量增益和相位特性曲線?
可調的實驗電源:Programmable Bench Pow
如何理解802.11ac 4×4?
matlab ac電源,基于MATLAB對AC/DC/AC電源的死區效應的諧波分析及仿真

matlab ac電源,基于MATLAB對AC/DC/AC電源的死區效應的諧波分析及仿真

從仿真器的角度理解Verilog語言1
從仿真器的角度理解Verilog語言2




 對OP AC特性仿真Bench的理解
對OP AC特性仿真Bench的理解











評論