什么是數？

2是一個數嗎？肯定是的咯。 那“二”呢？“two”呢？ 相信你能感覺到，它們不但都是數，而且是在用不同的記號表達著同樣的一個“東西”，即那個我們數兩個蘋果或兩個梨時天然感覺到的量。這個感覺說不清道不明，但真真切切地存在——誰都會數數嘛。

這就麻煩了，如何刻畫、把握與定義一個說不清道不明的東西呢？哲學家維特根斯坦（Wittgenstein）有言“一個詞的含義是它在語言中的用法”。

在工程界也有著所謂鴨子測試（Duck Test）的準則：如果一個事物看起來像鴨子、游起來像鴨子、叫起來也像鴨子，那它就是個鴨子。這指引著我們通過概念的性質來定義概念本身。

我們通過性質來定義概念。

換言之，我們不關心一個概念是什么，而關心它滿足什么。正是概念滿足的性質定義了這個概念本身。

為什么要這樣呢？因為可能有很多具體的對象都承載著我們關心的概念，這個概念不是其中任何一個具體對象，而是所有這些對象所共同承載著的那個存在，其彰顯于這些對象所共同具有的性質。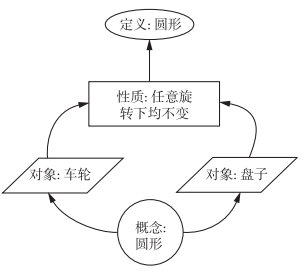



如圖所示，如果我們要定義概念“圓形”，會發現它既不是“盤子”，也不是“車輪”，而是盤子與車輪所共享的那種怎么轉都不變的形狀。關于定義的這一點認識對后文進入抽象世界至關重要。

除此之外，我們不描述概念是什么還有一個很重要的原因——很遺憾，我們可能永遠無法知道某個概念真正是什么。

最經典的例子當屬柏拉圖（Plato）的洞穴寓言（allegory of the cave）。

想象你自打出生便被關在一個洞穴里，洞口有一塊峭壁，陽光將洞外人們日常生活的影子打在這塊峭壁上。日復一日，你能看到的世界只有這塊二維峭壁上的倒影，誠然其中有日出日落、陰晴圓缺、人頭攢動…… 那些都只是表象，只是我們這個“更加真實”的三維世界在你的二維世界中的投影！很遺憾，你永遠不可能知道這些，你永遠不可能真正知道峭壁上的那些活動著的東西是什么。

基于以上兩點，我們不談論概念是什么，而只關心其性質，并由此定義概念本身。

那么，我們選取哪些性質呢？不能太多，否則范圍縮得太窄而可能有遺漏；也不能太少，不然范圍太大就海納百川了。這道邊界劃在哪里呢？不要忘了，任何時候，當我們在談論一個概念時，一定是有語境、有上下文、有目的、有話題的。

我們基于所在討論的話題，選擇恰好充分的若干期望被滿足的性質來定義概念。

具體來說，我們現在要定義“數”，我們的語境是什么呢？是今天的天氣？是一二三四的味道？當然不是。我們能懵懂地感覺到，我們在談論的東西，關乎數（第三聲），關乎運算。 于是，如果一個東西能用于計數，還能進行加減乘除，那不管它是什么，于我們討論的話題就足以被稱為“數”了！

在加減乘除四則運算中，減是加的逆運算，除是乘的逆運算，故我們可以進一步將要求降低到能進行加法與乘法。于是，這些就是我們要找的那恰好充分的性質！ 數是這樣的存在，其可以用于計數，彼此間可以相加、相乘。反之，如此這般的存在，便可以被認為是數。

可這還沒完，那什么叫“計數”，什么又叫“相加”“相乘”呢？我們先來看第一個問題。 門前大橋下，游過一群鴨。快來快來數一數，二四六七八。這首膾炙人口的兒歌想必你能哼出來。相比于一、二、三、四、五這些數（第四聲），一個、兩個、三個、四個、五個地數（第三聲），幾乎是生而為人與生俱來的能力。計數不過就是數數的同義詞。作為如此習以為常的天生能力，要如何定義數數呢？

讓我們來想一想，數數時數到的“二”，其本質是個什么。英國人叫其“two”，所以顯然“二”“two”這些名稱本身并無關乎其本質。還有一個角度，我們可以說“二”是“一”后面的那個數，是“三”前面的那個數。 那什么是“一”，什么又是“三”呢？什么是“前面”，什么又是“后面”呢？ 仿佛到了一個死胡同。看來我們不能盯著“一”“二”“三”這些具體的孤立數字不放，而是要把視角抬高，先把“數數”這個概念明確了！畢竟每一個數的存在是由數數這個概念的存在衍生來的。不難發現，數數這個概念完全由如下兩個性質刻畫：

1. 有一個計數的開始；

2. 我們可以一個一個不停地數下去。

基于此，我們可以做出如下定義：

? 定義“一”為第一點所規定的那個計數的開始；

? 定義“二”為從“一”數下去的下一個對象；

? 定義“三”為從“二”數下去的下一個對象；

? …… 拋開措辭不談，深究起來，這里還有問題。這個定義并沒有排除一種可能性： 數著數著會不會兜回來？一、二、三、二？也即，一個數的下一個數會不會等于之前的某個數？光看定義是有這種可能的，雖然我們可以說這一點已經被“能不停地數下去”所排除，因為不然的話，我們數數就變成“一二三二三二……”，沒有“下去”呀！ 話雖如此，但想必你也意識到了，這正是自然語言的模糊與歧義所在，根本沒有辦法用它來明確定義如數數這般已然模糊不清難以明言的人類本能。使用一種更加純粹、規范、無歧義的語言勢在必行！

語言是什么？

要上手一門新的語言，第一步自然是要掌握這個語言的字母、單詞和語法。數學這門語言的字母、單詞和語法，統稱為形式。

何謂形式？

形式（form）即無意義的符號（symbol）。

那進而何謂符號？

符號即有限長度的字符序列（sequence of letters）。

那又何謂字符序列呢？

這就觸及這本書的邊界了——我們不再嘗試對“字符序列”加以定義，而是需要由你訴諸自己的直覺來理解。比如，“你好”就是一個由兩個字符“你”與“好”組成的字符序列。

當然，我們一看到它便會立馬不自覺地為其賦予意義，知道它是在表達打招呼的意思。

不妨再來看個符號：“KILIG”，這是一個由五個字符構成的符號，它對你來說完全沒有意義了吧！它不是英文，而是來自一個叫 Tagalog 的菲律賓呂宋島中部的民族。對于那里的人們，這個符號是有意義的，用于形容浪漫或有趣的事情發生后肚子里仿佛有蝴蝶在飛舞一般的感覺。

從這兩例我們能看到，符號與其意義是兩件獨立的事情，符號本身是沒有意義的，以純粹形式存在，只有當它被置于一個語境之中后，才獲得了意義。 讓我們再來看一個例子。考察 1 + 1 = 2 這個斷言。 它成立嗎？當然成立！ 可是要知道，僅當我們賦予了 1、2、+、= 這些符號我們慣常的含義后，它才成了一個算術意義上正確的等式。

但在形式上它顯然是不成立的！為啥？因為即使我們為 = 賦予了慣常的“等于”之含義，其左邊有三個字符1、+、1，右邊只有一個字符 2，當然是不同的字符序列呀！

有了一堆符號后，我們首先能做的便是隨意組合它們。比如，給你兩個符號 和 ，我們能組合出如下這些：, , , , , · · · 再比如，給你三個符號“你”“好”“呀”，我們能組合出你好，你好呀，呀好你，好呀你，你呀呀，好好好, · · · 然而，并不是所有的組合都應被采納。

比如第二個例子中，若我們是想研究中 文，那么顯然只有“你好”“你好呀”可以接受，“呀好你”這種胡言亂語應該被丟掉。這種對符號組合進行的選擇，便是我們俗稱的語法。 再以英語為例。假如我們有符號 I, l, o, v, e, y, u 以及空格，我們可以組合出：I love you，I you love，you love I，ouyi evool uy，… 顯然，只有第一句是合乎語法的。

語法（grammar）是對符號組合的選擇。我們稱符號組合為公式（formula）。稱符合語法的公式為合式公式（well-formed formula）。

至此，我們有了字母、單詞和語法，一門語言便誕生了！ 形式語言（formal language）由如下兩部分構成：

? 由有限個符號構成的字母表（alphabet），

? 一個語法。

進而，我們說：數學是一門形式語言。

審核編輯：劉清