FFT(Fast Fourier Transform),快速傅立葉變換,是一種 DFT(離散傅里葉變換)的高效算法。在以時頻變換分析為基礎的數字處理方法中,有著不可替代的作用。
FFT 原理
◆公式推導
DFT 的運算公式為:
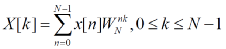
其中,
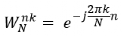
將離散傅里葉變換公式拆分成奇偶項,則前 N/2 個點可以表示為:
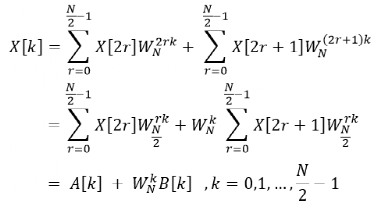
同理,后 N/2 個點可以表示為:
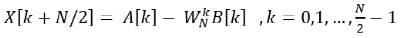
由此可知,后 N/2 個點的值完全可以通過計算前 N/2 個點時的中間過程值確定。對 A[k] 與 B[k] 繼續進行奇偶分解,直至變成 2 點的 DFT,這樣就可以避免很多的重復計算,實現了快速離散傅里葉變換(FFT)的過程。
◆算法結構
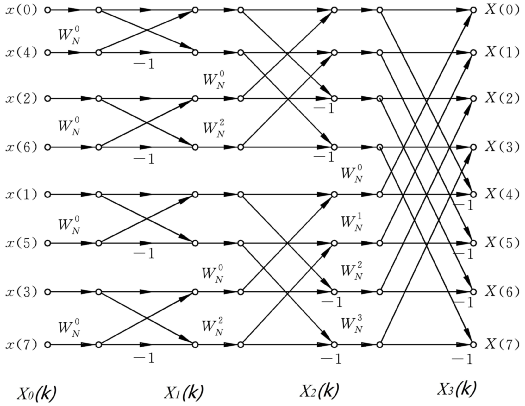
8 點 FFT 計算的結構示意圖如下。
由圖可知,只需要簡單的計算幾次乘法和加法,便可完成離散傅里葉變換過程,而不是對每個數據進行繁瑣的相乘和累加。
◆重要特性
(1) 級的概念
每分割一次,稱為一級運算。
設 FFT 運算點數為 N,共有 M 級運算,則它們滿足:
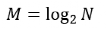
每一級運算的標識為 m = 0, 1, 2, ..., M-1。
為了便于分割計算,FFT 點數 N 的取值經常為 2 的整數次冪。
(2) 蝶形單元
FFT 計算結構由若干個蝶形運算單元組成,每個運算單元示意圖如下:
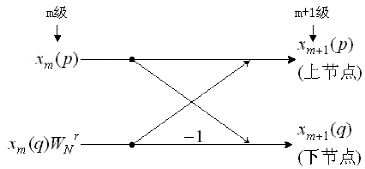
蝶形單元的輸入輸出滿足:
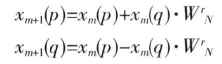
其中,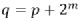 。
。
每一個蝶形單元運算時,進行了一次乘法和兩次加法。
每一級中,均有 N/2 個蝶形單元。
故完成一次 FFT 所需要的乘法次數和加法次數分別為:
(3) 組的概念
每一級 N/2 個蝶形單元可分為若干組,每一組有著相同的結構與因子分布。
例如 m=0 時,可以分為 N/2=4 組。
m=1 時,可以分為 N/4=2 組。
m=M-1 時,此時只能分為 1 組。
(4) 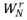 因子分布
因子分布
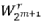 因子存在于 m 級,其中
因子存在于 m 級,其中 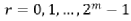 。
。
在 8 點 FFT 第二級運算中,即 m=1 ,蝶形運算因子可以化簡為:
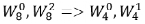
(5) 碼位倒置
對于 N=8 點的 FFT 計算,X(0) ~ X(7) 位置對應的 2 進制碼為:
X(000), X(001), X(010), X(011), X(100), X(101), X(110), X(111)
將其位置的 2 進制碼進行翻轉:
X(000), X(100), X(010), X(110), X(001), X(101), X(011), X(111)
此時位置對應的 10 進制為:
X(0), X(4), X(2), X(6), X(1), X(5), X(3), X(7)
恰好對應 FFT 第一級輸入數據的順序。
該特性有利于 FFT 的編程實現。
FFT 設計
◆設計說明
為了利用仿真簡單的說明 FFT 的變換過程,數據點數取較小的值 8。
如果數據是串行輸入,需要先進行緩存,所以設計時數據輸入方式為并行。
數據輸入分為實部和虛部共 2 部分,所以計算結果也分為實部和虛部。
設計采用流水結構,暫不考慮資源消耗的問題。
為了使設計結構更加簡單,這里做一步妥協,乘法計算直接使用乘號。如果 FFT 設計應用于實際,一定要將乘法結構換成可以流水的乘法器,或使用官方提供的效率較高的乘法器 IP。
◆蝶形單元設計
蝶形單元為定點運算,需要對旋轉因子進行定點量化。
借助 matlab 將旋轉因子擴大 8192 倍(左移 13 位),可參考附錄。
為了防止蝶形運算中的乘法和加法導致位寬逐級增大,每一級運算完成后,要對輸出數據進行固定位寬的截位,也可去掉旋轉因子倍數增大而帶來的影響。
代碼如下:
`timescale 1ns/100ps
/**************** butter unit *************************
Xm(p) ------------------------ > Xm+1(p)
- - >
- -
-
- -
- - >
Xm(q) ------------------------ > Xm+1(q)
Wn -1
*//////////////////////////////////////////////////////
module butterfly
(
input clk,
input rstn,
input en,
input signed [23:0] xp_real, // Xm(p)
input signed [23:0] xp_imag,
input signed [23:0] xq_real, // Xm(q)
input signed [23:0] xq_imag,
input signed [15:0] factor_real, // Wnr
input signed [15:0] factor_imag,
output valid,
output signed [23:0] yp_real, //Xm+1(p)
output signed [23:0] yp_imag,
output signed [23:0] yq_real, //Xm+1(q)
output signed [23:0] yq_imag);
reg [4:0] en_r ;
always @(posedge clk or negedge rstn) begin
if (!rstn) begin
en_r <= 'b0 ;
end
else begin
en_r <= {en_r[3:0], en} ;
end
end
//=====================================================//
//(1.0) Xm(q) mutiply and Xm(p) delay
reg signed [39:0] xq_wnr_real0;
reg signed [39:0] xq_wnr_real1;
reg signed [39:0] xq_wnr_imag0;
reg signed [39:0] xq_wnr_imag1;
reg signed [39:0] xp_real_d;
reg signed [39:0] xp_imag_d;
always @(posedge clk or negedge rstn) begin
if (!rstn) begin
xp_real_d <= 'b0;
xp_imag_d <= 'b0;
xq_wnr_real0 <= 'b0;
xq_wnr_real1 <= 'b0;
xq_wnr_imag0 <= 'b0;
xq_wnr_imag1 <= 'b0;
end
else if (en) begin
xq_wnr_real0 <= xq_real * factor_real;
xq_wnr_real1 <= xq_imag * factor_imag;
xq_wnr_imag0 <= xq_real * factor_imag;
xq_wnr_imag1 <= xq_imag * factor_real;
//expanding 8192 times as Wnr
xp_real_d <= {{4{xp_real[23]}}, xp_real[22:0], 13'b0};
xp_imag_d <= {{4{xp_imag[23]}}, xp_imag[22:0], 13'b0};
end
end
//(1.1) get Xm(q) mutiplied-results and Xm(p) delay again
reg signed [39:0] xp_real_d1;
reg signed [39:0] xp_imag_d1;
reg signed [39:0] xq_wnr_real;
reg signed [39:0] xq_wnr_imag;
always @(posedge clk or negedge rstn) begin
if (!rstn) begin
xp_real_d1 <= 'b0;
xp_imag_d1 <= 'b0;
xq_wnr_real <= 'b0 ;
xq_wnr_imag <= 'b0 ;
end
else if (en_r[0]) begin
xp_real_d1 <= xp_real_d;
xp_imag_d1 <= xp_imag_d;
//提前設置好位寬余量,防止數據溢出
xq_wnr_real <= xq_wnr_real0 - xq_wnr_real1 ;
xq_wnr_imag <= xq_wnr_imag0 + xq_wnr_imag1 ;
end
end
//======================================================//
//(2.0) butter results
reg signed [39:0] yp_real_r;
reg signed [39:0] yp_imag_r;
reg signed [39:0] yq_real_r;
reg signed [39:0] yq_imag_r;
always @(posedge clk or negedge rstn) begin
if (!rstn) 



 Verilog FFT設計方案
Verilog FFT設計方案