到目前為止,我們已經用小批量隨機梯度下降訓練了我們的模型。然而,當我們實現該算法時,我們只擔心通過模型進行前向傳播所涉及的計算。當需要計算梯度時,我們只是調用了深度學習框架提供的反向傳播函數。
梯度的自動計算(自動微分)大大簡化了深度學習算法的實現。在自動微分之前,即使是對復雜模型的微小改動也需要手動重新計算復雜的導數。令人驚訝的是,學術論文常常不得不分配大量頁面來推導更新規則。雖然我們必須繼續依賴自動微分,以便我們可以專注于有趣的部分,但如果您想超越對深度學習的膚淺理解,您應該知道這些梯度是如何在底層計算的。
在本節中,我們將深入探討反向傳播(通常稱為反向傳播)的細節。為了傳達對技術及其實現的一些見解,我們依賴于一些基本的數學和計算圖。首先,我們將重點放在具有權重衰減的單隱藏層 MLP 上(?2 正則化,將在后續章節中描述)。
5.3.1. 前向傳播
前向傳播(或forward pass)是指神經網絡從輸入層到輸出層依次計算和存儲中間變量(包括輸出)。我們現在逐步了解具有一個隱藏層的神經網絡的機制。這可能看起來很乏味,但用放克演奏家詹姆斯布朗的永恒名言來說,你必須“付出代價才能成為老板”。
為了簡單起見,我們假設輸入示例是 x∈Rd并且我們的隱藏層不包含偏差項。這里的中間變量是:
(5.3.1)z=W(1)x,
在哪里W(1)∈Rh×d是隱藏層的權重參數。運行中間變量后 z∈Rh通過激活函數 ?我們獲得了長度的隱藏激活向量h,
(5.3.2)h=?(z).
隱藏層輸出h也是一個中間變量。假設輸出層的參數只具有權重W(2)∈Rq×h,我們可以獲得一個輸出層變量,其向量長度為q:
(5.3.3)o=W(2)h.
假設損失函數是l示例標簽是 y,然后我們可以計算單個數據示例的損失項,
(5.3.4)L=l(o,y).
根據定義?2我們稍后將介紹的正則化,給定超參數λ,正則化項是
(5.3.5)s=λ2(‖W(1)‖F2+‖W(2)‖F2),
其中矩陣的 Frobenius 范數就是?2將矩陣展平為向量后應用范數。最后,模型在給定數據示例上的正則化損失為:
(5.3.6)J=L+s.
我們指的是J作為下面討論中的目標函數。
5.3.2. 前向傳播的計算圖
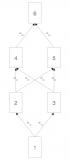
繪制計算圖有助于我們可視化計算中運算符和變量的依賴關系。圖 5.3.1 包含與上述簡單網絡相關的圖形,其中方塊表示變量,圓圈表示運算符。左下角表示輸入,右上角表示輸出。請注意箭頭的方向(說明數據流)主要是向右和向上。
圖 5.3.1前向傳播計算圖。
5.3.3. 反向傳播
反向傳播是指計算神經網絡參數梯度的方法。簡而言之,該方法根據微 積分的鏈式法則以相反的順序遍歷網絡,從輸出層到輸入層。該算法存儲計算某些參數的梯度時所需的任何中間變量(偏導數)。假設我們有函數 Y=f(X)和Z=g(Y), 其中輸入和輸出 X,Y,Z是任意形狀的張量。通過使用鏈式法則,我們可以計算導數 Z關于X通過
(5.3.7)?Z?X=prod(?Z?Y,?Y?X).
在這里我們使用prod運算符在執行必要的操作(例如轉置和交換輸入位置)后將其參數相乘。對于向量,這很簡單:它只是矩陣-矩陣乘法。對于更高維的張量,我們使用適當的對應物。運營商 prod隱藏所有符號開銷。
回想一下,具有一個隱藏層的簡單網絡的參數,其計算圖如圖 5.3.1所示,是 W(1)和W(2). 反向傳播的目的是計算梯度 ?J/?W(1)和 ?J/?W(2). 為此,我們應用鏈式法則并依次計算每個中間變量和參數的梯度。計算的順序相對于前向傳播中執行的順序是相反的,因為我們需要從計算圖的結果開始并朝著參數的方向努力。第一步是計算目標函數的梯度J=L+s關于損失期限 L和正則化項s.
(5.3.8)?J?L=1and?J?s=1.
接下來,我們計算目標函數相對于輸出層變量的梯度o根據鏈式法則:
(5.3.9)?J?o=prod(?J?L,?L?o)=?L?o∈Rq.
接下來,我們計算關于兩個參數的正則化項的梯度:
(5.3.10)?s?W(1)=λW(1)and?s?W(2)=λW(2).
現在我們可以計算梯度了 ?J/?W(2)∈Rq×h 最接近輸出層的模型參數。使用鏈式規則產生:
(5.3.11)?J?W(2)=prod(?J?o,?o?W(2))+prod(?J?s,?s?W(2))=?J?oh?+λW(2).
獲得關于的梯度W(1)我們需要繼續沿著輸出層反向傳播到隱藏層。關于隱藏層輸出的梯度 ?J/?h∈Rh是(誰)給的
(5.3.12)?J?h=prod(?J?o,?o?h)=W(2)??J?o.
由于激活函數?按元素應用,計算梯度 ?J/?z∈Rh中間變量的z要求我們使用逐元素乘法運算符,我們用⊙:
(5.3.13)?J?z=prod(?J?h,?h?z)=?J?h⊙?′(z).
最后,我們可以得到梯度 ?J/?W(1)∈Rh×d 最接近輸入層的模型參數。根據鏈式法則,我們得到
(5.3.14)?J?W(1)=prod(?J?z,?z?W(1))+prod(?J?s,?s?W(1))=?J?zx?+λW(1).
5.3.4. 訓練神經網絡
在訓練神經網絡時,前向傳播和反向傳播相互依賴。特別是,對于前向傳播,我們沿依賴方向遍歷計算圖并計算其路徑上的所有變量。然后將這些用于反向傳播,其中圖上的計算順序是相反的。
以前述簡單網絡為例進行說明。一方面,在前向傳播過程中計算正則化項(5.3.5) 取決于模型參數的當前值W(1)和W(2). 它們由優化算法根據最近一次迭代中的反向傳播給出。另一方面,反向傳播過程中參數(5.3.11)的梯度計算取決于隱藏層輸出的當前值h,這是由前向傳播給出的。
因此在訓練神經網絡時,在初始化模型參數后,我們交替進行正向傳播和反向傳播,使用反向傳播給出的梯度更新模型參數。請注意,反向傳播會重用前向傳播中存儲的中間值以避免重復計算。結果之一是我們需要保留中間值,直到反向傳播完成。這也是為什么訓練比普通預測需要更多內存的原因之一。此外,這些中間值的大小大致與網絡層數和批量大小成正比。因此,使用更大的批量大小訓練更深的網絡更容易導致內存不足錯誤。
5.3.5. 概括
前向傳播在神經網絡定義的計算圖中順序計算和存儲中間變量。它從輸入層進行到輸出層。反向傳播以相反的順序順序計算并存儲神經網絡中中間變量和參數的梯度。在訓練深度學習模型時,正向傳播和反向傳播是相互依賴的,訓練需要的內存明顯多于預測。
5.3.6. 練習
假設輸入X一些標量函數 f是n×m矩陣。梯度的維數是多少f關于X?
向本節中描述的模型的隱藏層添加偏差(您不需要在正則化項中包含偏差)。
畫出相應的計算圖。
推導前向和反向傳播方程。
計算本節中描述的模型中訓練和預測的內存占用量。
假設您要計算二階導數。計算圖會發生什么變化?您預計計算需要多長時間?
假設計算圖對于您的 GPU 來說太大了。
您可以將它分區到多個 GPU 上嗎?
與在較小的 minibatch 上進行訓練相比,優缺點是什么?
審核編輯黃宇
Discussions
-
pytorch
+關注
關注
2文章
808瀏覽量
13239
發布評論請先 登錄
相關推薦
解讀多層神經網絡反向傳播原理




 PyTorch教程-5.3. 前向傳播、反向傳播和計算圖
PyTorch教程-5.3. 前向傳播、反向傳播和計算圖

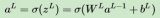












評論