如果您完成了第 9.5 節中的練習,您會發現梯度裁剪對于防止偶爾出現的大量梯度破壞訓練穩定性至關重要。我們暗示爆炸梯度源于長序列的反向傳播。在介紹大量現代 RNN 架構之前,讓我們仔細看看反向傳播在數學細節中是如何在序列模型中工作的。希望這個討論能使梯度消失和爆炸的概念更加精確。如果你還記得我們在 5.3 節介紹 MLP 時通過計算圖進行前向和反向傳播的討論,那么 RNN 中的前向傳播應該相對簡單。在 RNN 中應用反向傳播稱為 時間反向傳播 ( Werbos, 1990 ). 此過程要求我們一次擴展(或展開)RNN 的計算圖。展開的 RNN 本質上是一個前饋神經網絡,具有相同的參數在整個展開的網絡中重復出現的特殊屬性,出現在每個時間步長。然后,就像在任何前饋神經網絡中一樣,我們可以應用鏈式法則,通過展開的網絡反向傳播梯度。每個參數的梯度必須在參數出現在展開網絡中的所有位置上求和。從我們關于卷積神經網絡的章節中應該熟悉處理這種權重綁定。
出現并發癥是因為序列可能相當長。處理由超過一千個標記組成的文本序列并不罕見。請注意,從計算(太多內存)和優化(數值不穩定)的角度來看,這都會帶來問題。第一步的輸入在到達輸出之前要經過 1000 多個矩陣乘積,還需要另外 1000 個矩陣乘積來計算梯度。我們現在分析可能出現的問題以及如何在實踐中解決它。
9.7.1. RNN 中的梯度分析
我們從 RNN 工作原理的簡化模型開始。該模型忽略了有關隱藏狀態細節及其更新方式的細節。這里的數學符號沒有明確區分標量、向量和矩陣。我們只是想培養一些直覺。在這個簡化模型中,我們表示ht作為隱藏狀態, xt作為輸入,和ot作為時間步的輸出t. 回憶一下我們在第 9.4.2 節中的討論,輸入和隱藏狀態可以在乘以隱藏層中的一個權重變量之前連接起來。因此,我們使用 wh和wo分別表示隱藏層和輸出層的權重。因此,每個時間步的隱藏狀態和輸出是
(9.7.1)ht=f(xt,ht?1,wh),ot=g(ht,wo),
在哪里f和g分別是隱藏層和輸出層的變換。因此,我們有一個價值鏈 {…,(xt?1,ht?1,ot?1),(xt,ht,ot),…} 通過循環計算相互依賴。前向傳播相當簡單。我們所需要的只是遍歷(xt,ht,ot)一次三倍一個時間步長。輸出之間的差異ot和想要的目標 yt然后通過所有的目標函數進行評估 T時間步長為
(9.7.2)L(x1,…,xT,y1,…,yT,wh,wo)=1T∑t=1Tl(yt,ot).
對于反向傳播,事情有點棘手,尤其是當我們計算關于參數的梯度時wh目標函數的L. 具體來說,根據鏈式法則,
(9.7.3)?L?wh=1T∑t=1T?l(yt,ot)?wh=1T∑t=1T?l(yt,ot)?ot?g(ht,wo)?ht?ht?wh.
(9.7.3)中乘積的第一和第二個因子 很容易計算。第三個因素 ?ht/?wh事情變得棘手了,因為我們需要循環計算參數的影響wh在 ht. 根據 (9.7.1)中的循環計算,ht取決于兩者ht?1 和wh, 其中計算ht?1也取決于 wh. 因此,評估的總導數ht關于wh使用鏈式規則收益率
(9.7.4)?ht?wh=?f(xt,ht?1,wh)?wh+?f(xt,ht?1,wh)?ht?1?ht?1?wh.
為了推導上述梯度,假設我們有三個序列 {at},{bt},{ct}令人滿意a0=0和 at=bt+ctat?1為了t=1,2,…. 然后為 t≥1, 很容易證明
(9.7.5)at=bt+∑i=1t?1(∏j=i+1tcj)bi.
通過替換at,bt, 和ct根據
(9.7.6)at=?ht?wh,bt=?f(xt,ht?1,wh)?wh,ct=?f(xt,ht?1,wh)?ht?1,
(9.7.4)中的梯度計算 滿足at=bt+ctat?1. 因此,根據 (9.7.5) ,我們可以刪除(9.7.4)中的循環計算
(9.7.7)?ht?wh=?f(xt,ht?1,wh)?wh+∑i=1t?1(∏j=i+1t?f(xj,hj?1,wh)?hj?1)?f(xi,hi?1,wh)?wh.
雖然我們可以使用鏈式法則來計算 ?ht/?wh遞歸地,這條鏈會變得很長t很大。讓我們討論一些處理這個問題的策略。
9.7.1.1. 全計算
一個想法可能是計算(9.7.7)中的總和 。然而,這是非常緩慢的,梯度可能會爆炸,因為初始條件的細微變化可能會對結果產生很大影響。也就是說,我們可以看到類似于蝴蝶效應的現象,即初始條件的微小變化會導致結果發生不成比例的變化。這通常是不希望的。畢竟,我們正在尋找能夠很好泛化的穩健估計器。因此,這種策略幾乎從未在實踐中使用過。
9.7.1.2. 截斷時間步長
或者,我們可以在(9.7.7)之后截斷總和 τ腳步。這是我們迄今為止一直在討論的內容。這導致了對真實梯度的近似,簡單地通過終止總和 ?ht?τ/?wh. 在實踐中,這非常有效。這就是通常所說的隨時間截斷的反向傳播( Jaeger, 2002 )。這樣做的后果之一是該模型主要關注短期影響而不是長期后果。這實際上是可取的,因為它會使估計偏向于更簡單和更穩定的模型。
9.7.1.3. 隨機截斷
最后,我們可以更換?ht/?wh通過一個隨機變量,它在預期中是正確的但截斷了序列。這是通過使用一系列ξt預定義的 0≤πt≤1, 在哪里P(ξt=0)=1?πt和 P(ξt=πt?1)=πt, 因此E[ξt]=1. 我們用這個來代替漸變?ht/?wh在 (9.7.4)中與
(9.7.8)zt=?f(xt,ht?1,wh)?wh+ξt?f(xt,ht?1,wh)?ht?1?ht?1?wh.
它遵循的定義ξt那 E[zt]=?ht/?wh. 每當ξt=0 循環計算在該時間步終止t. 這導致了不同長度序列的加權和,其中長序列很少見但適當超重。這個想法是由Tallec 和 Ollivier ( 2017 )提出的。
9.7.1.4. 比較策略
圖 9.7.1比較 RNN 中計算梯度的策略。從上到下:隨機截斷、規則截斷和全計算。
圖 9.7.1說明了使用 RNN 的時間反向傳播分析時間機器的前幾個字符時的三種策略
第一行是將文本分成不同長度的段的隨機截斷。
第二行是將文本分成相同長度的子序列的常規截斷。這就是我們在 RNN 實驗中一直在做的事情。
第三行是通過時間的完整反向傳播,導致計算上不可行的表達式。
不幸的是,雖然在理論上很有吸引力,但隨機截斷并沒有比常規截斷好多少,這很可能是由于多種因素造成的。首先,經過多次反向傳播步驟后觀察到的效果足以在實踐中捕獲依賴關系。其次,增加的方差抵消了更多步驟梯度更準確的事實。第三,我們實際上想要只有小范圍交互的模型。因此,隨著時間的推移定期截斷的反向傳播具有輕微的正則化效果,這可能是理想的。
9.7.2. 詳細的時間反向傳播
討論完一般原理后,讓我們詳細討論時間反向傳播。與9.7.1節的分析不同 ,下面我們將展示如何計算目標函數對所有分解模型參數的梯度。為了簡單起見,我們考慮一個沒有偏置參數的 RNN,其隱藏層中的激活函數使用恒等映射(?(x)=x). 對于時間步t, 讓單個示例輸入和目標為 xt∈Rd和yt, 分別。隱藏狀態ht∈Rh和輸出 ot∈Rq被計算為
(9.7.9)ht=Whxxt+Whhht?1,ot=Wqhht,
在哪里Whx∈Rh×d, Whh∈Rh×h, 和 Wqh∈Rq×h是權重參數。表示為l(ot,yt)時間步長的損失 t. 我們的目標函數,損失超過T因此,從序列開始的時間步長是
(9.7.10)L=1T∑t=1Tl(ot,yt).
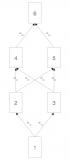
為了可視化RNN計算過程中模型變量和參數之間的依賴關系,我們可以為模型繪制計算圖,如圖9.7.2所示。例如,時間步長 3 的隱藏狀態的計算, h3, 取決于模型參數 Whx和Whh, 最后一個時間步的隱藏狀態h2, 和當前時間步長的輸入x3.
圖 9.7.2顯示具有三個時間步長的 RNN 模型的依賴關系的計算圖。方框代表變量(未加陰影)或參數(加陰影),圓圈代表運算符。
正如剛才提到的,圖 9.7.2中的模型參數是 Whx,Whh, 和 Wqh. 通常,訓練此模型需要針對這些參數進行梯度計算 ?L/?Whx, ?L/?Whh, 和 ?L/?Wqh. 根據圖 9.7.2中的依賴關系,我們可以沿箭頭相反的方向遍歷,依次計算并存儲梯度。為了在鏈式法則中靈活表達不同形狀的矩陣、向量和標量的乘法,我們繼續使用 prod操作員如第 5.3 節所述。
首先,在任何時間步根據模型輸出對目標函數進行微分t相當簡單:
(9.7.11)?L?ot=?l(ot,yt)T??ot∈Rq.
現在,我們可以計算目標相對于參數的梯度Wqh在輸出層: ?L/?Wqh∈Rq×h. 根據圖 9.7.2,目標L依賴于取決于 Wqh通過o1,…,oT. 使用鏈式規則收益率
(9.7.12)?L?Wqh=∑t=1Tprod(?L?ot,?ot?Wqh)=∑t=1T?L?otht?,
在哪里?L/?ot由(9.7.11)給出 。
接下來,如圖9.7.2所示,在最后的時間步 T, 目標函數L取決于隱藏狀態 hT只能通過oT. 因此,我們很容易找到梯度 ?L/?hT∈Rh使用鏈式法則:
(9.7.13)?L?hT=prod(?L?oT,?oT?hT)=Wqh??L?oT.
任何時間步長都會變得更加棘手t
(9.7.14)?L?ht=prod(?L?ht+1,?ht+1?ht)+prod(?L?ot,?ot?ht)=Whh??L?ht+1+Wqh??L?ot.
為了分析,擴展任何時間步長的循環計算 1≤t≤T給
(9.7.15)?L?ht=∑i=tT(Whh?)T?iWqh??L?oT+t?i.
我們可以從(9.7.15)中看到,這個簡單的線性示例已經展示了長序列模型的一些關鍵問題:它涉及潛在的非常大的冪Whh?. 其中,小于 1 的特征值消失,大于 1 的特征值發散。這在數值上是不穩定的,表現為梯度消失和爆炸。如第 9.7.1 節所述,解決此問題的一種方法是將時間步長截斷為便于計算的大小。實際上,這種截斷也可以通過在給定數量的時間步后分離梯度來實現。稍后,我們將看到更復雜的序列模型(如長短期記憶)如何進一步緩解這種情況。
最后,圖 9.7.2表明目標函數 L取決于模型參數Whx和 Whh通過隱藏狀態在隱藏層中 h1,…,hT. 計算關于這些參數的梯度 ?L/?Whx∈Rh×d 和 ?L/?Whh∈Rh×h,我們應用給出的鏈式規則
(9.7.16)?L?Whx=∑t=1Tprod(?L?ht,?ht?Whx)=∑t=1T?L?htxt?,?L?Whh=∑t=1Tprod(?L?ht,?ht?Whh)=∑t=1T?L?htht?1?,
在哪里?L/?ht由(9.7.13)和 (9.7.14)循環計算的是影響數值穩定性的關鍵量。
由于時間反向傳播是反向傳播在 RNN 中的應用,正如我們在第 5.3 節中解釋的那樣,訓練 RNN 交替進行正向傳播和時間反向傳播。此外,通過時間的反向傳播依次計算并存儲上述梯度。具體來說就是復用存儲的中間值,避免重復計算,比如存儲 ?L/?ht用于兩者的計算?L/?Whx和 ?L/?Whh.
9.7.3. 概括
時間反向傳播僅僅是反向傳播對具有隱藏狀態的序列模型的應用。截斷是為了計算方便和數值穩定性所需要的,例如規則截斷和隨機截斷。矩陣的高次冪會導致特征值發散或消失。這以爆炸或消失梯度的形式表現出來。為了高效計算,中間值在反向傳播期間被緩存。
9.7.4. 練習
假設我們有一個對稱矩陣 M∈Rn×n具有特征值 λi其對應的特征向量是 vi(i=1,…,n). 不失一般性,假設它們按順序排列 |λi|≥|λi+1|.
顯示Mk有特征值λik.
證明對于一個隨機向量x∈Rn, 很有可能Mkx將與特征向量非常一致v1的 M. 將此聲明正式化。
上述結果對 RNN 中的梯度意味著什么?
除了梯度裁剪,你能想到任何其他方法來應對遞歸神經網絡中的梯度爆炸嗎?
Discussions
-
pytorch
+關注
關注
2文章
808瀏覽量
13317
發布評論請先 登錄
相關推薦
人工智能(AI)學習:如何講解BP(反向傳播)流程

淺析深度神經網絡(DNN)反向傳播算法(BP)
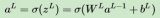
BP(BackPropagation)反向傳播神經網絡介紹及公式推導

PyTorch教程-5.3. 前向傳播、反向傳播和計算圖
神經網絡前向傳播和反向傳播區別
反向傳播神經網絡建模基本原理
神經網絡反向傳播算法的優缺點有哪些
【每天學點AI】前向傳播、損失函數、反向傳播





 PyTorch教程-9.7. 時間反向傳播
PyTorch教程-9.7. 時間反向傳播










評論