在前面的章節中,我們一直在訓練過程中使用隨機梯度下降,但是沒有解釋它為什么有效。為了闡明它,我們剛剛在第 12.3 節中描述了梯度下降的基本原理。在本節中,我們將繼續 更詳細地討論隨機梯度下降。
%matplotlib inline import math import torch from d2l import torch as d2l
%matplotlib inline import math from mxnet import np, npx from d2l import mxnet as d2l npx.set_np()
%matplotlib inline import math import tensorflow as tf from d2l import tensorflow as d2l
12.4.1。隨機梯度更新
在深度學習中,目標函數通常是訓練數據集中每個示例的損失函數的平均值。給定訓練數據集n例子,我們假設 fi(x)是關于 index 訓練樣例的損失函數i, 在哪里x是參數向量。然后我們到達目標函數
(12.4.1)f(x)=1n∑i=1nfi(x).
目標函數的梯度在x被計算為
(12.4.2)?f(x)=1n∑i=1n?fi(x).
如果使用梯度下降,每次自變量迭代的計算成本為O(n), 線性增長 n. 因此,當訓練數據集較大時,每次迭代的梯度下降代價會更高。
隨機梯度下降 (SGD) 減少了每次迭代的計算成本。在隨機梯度下降的每次迭代中,我們統一采樣一個索引i∈{1,…,n}隨機獲取數據示例,并計算梯度?fi(x)更新x:
(12.4.3)x←x?η?fi(x),
在哪里η是學習率。我們可以看到每次迭代的計算成本從O(n) 梯度下降到常數O(1). 此外,我們要強調的是隨機梯度 ?fi(x)是完整梯度的無偏估計?f(x)因為
(12.4.4)Ei?fi(x)=1n∑i=1n?fi(x)=?f(x).
這意味著,平均而言,隨機梯度是對梯度的良好估計。
現在,我們將通過向梯度添加均值為 0 和方差為 1 的隨機噪聲來模擬隨機梯度下降,將其與梯度下降進行比較。
def f(x1, x2): # Objective function return x1 ** 2 + 2 * x2 ** 2 def f_grad(x1, x2): # Gradient of the objective function return 2 * x1, 4 * x2 def sgd(x1, x2, s1, s2, f_grad): g1, g2 = f_grad(x1, x2) # Simulate noisy gradient g1 += torch.normal(0.0, 1, (1,)).item() g2 += torch.normal(0.0, 1, (1,)).item() eta_t = eta * lr() return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0) def constant_lr(): return 1 eta = 0.1 lr = constant_lr # Constant learning rate d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: 0.014749, x2: 0.009829
def f(x1, x2): # Objective function return x1 ** 2 + 2 * x2 ** 2 def f_grad(x1, x2): # Gradient of the objective function return 2 * x1, 4 * x2 def sgd(x1, x2, s1, s2, f_grad): g1, g2 = f_grad(x1, x2) # Simulate noisy gradient g1 += np.random.normal(0.0, 1, (1,)) g2 += np.random.normal(0.0, 1, (1,)) eta_t = eta * lr() return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0) def constant_lr(): return 1 eta = 0.1 lr = constant_lr # Constant learning rate d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: -0.472513, x2: 0.110780
def f(x1, x2): # Objective function return x1 ** 2 + 2 * x2 ** 2 def f_grad(x1, x2): # Gradient of the objective function return 2 * x1, 4 * x2 def sgd(x1, x2, s1, s2, f_grad): g1, g2 = f_grad(x1, x2) # Simulate noisy gradient g1 += tf.random.normal([1], 0.0, 1) g2 += tf.random.normal([1], 0.0, 1) eta_t = eta * lr() return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0) def constant_lr(): return 1 eta = 0.1 lr = constant_lr # Constant learning rate d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: -0.103750, x2: 0.054715
正如我們所見,隨機梯度下降中變量的軌跡比我們在12.3 節中觀察到的梯度下降中的軌跡噪聲大得多。這是由于梯度的隨機性。也就是說,即使我們到達最小值附近,我們仍然受到瞬時梯度注入的不確定性的影響η?fi(x). 即使在 50 步之后,質量仍然不是很好。更糟糕的是,它不會在額外的步驟后得到改善(我們鼓勵您嘗試更多的步驟來確認這一點)。這給我們留下了唯一的選擇:改變學習率η. 但是,如果我們選擇的太小,我們最初不會取得任何有意義的進展。另一方面,如果我們選擇太大,我們將得不到好的解決方案,如上所示。解決這些相互沖突的目標的唯一方法是隨著優化的進行動態降低學習率。
lr這也是在step函數中加入學習率函數的原因sgd。在上面的例子中,學習率調度的任何功能都處于休眠狀態,因為我們將相關lr 函數設置為常量。
12.4.2。動態學習率
更換η具有隨時間變化的學習率 η(t)增加了控制優化算法收斂的復雜性。特別是,我們需要弄清楚多快 η應該腐爛。如果太快,我們將過早地停止優化。如果我們減少它太慢,我們會在優化??上浪費太多時間。以下是一些用于調整的基本策略η隨著時間的推移(我們稍后會討論更高級的策略):
(12.4.5)η(t)=ηiifti≤t≤ti+1piecewise constantη(t)=η0?e?λtexponential decayη(t)=η0?(βt+1)?αpolynomial decay
在第一個分段常數場景中,我們降低學習率,例如,每當優化進展停滯時。這是訓練深度網絡的常用策略。或者,我們可以通過指數衰減更積極地減少它。不幸的是,這通常會導致在算法收斂之前過早停止。一個流行的選擇是多項式衰減α=0.5. 在凸優化的情況下,有許多證據表明該比率表現良好。
讓我們看看指數衰減在實踐中是什么樣子的。
def exponential_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return math.exp(-0.1 * t) t = 1 lr = exponential_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
epoch 1000, x1: -0.878960, x2: -0.023958
def exponential_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return math.exp(-0.1 * t) t = 1 lr = exponential_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
epoch 1000, x1: -0.820458, x2: 0.004701
def exponential_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return math.exp(-0.1 * t) t = 1 lr = exponential_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
epoch 1000, x1: -0.798681, x2: -0.067649
正如預期的那樣,參數的方差顯著減少。然而,這是以無法收斂到最優解為代價的x=(0,0). 即使在 1000 次迭代之后,我們仍然離最佳解決方案很遠。實際上,該算法根本無法收斂。另一方面,如果我們使用多項式衰減,其中學習率隨步數的平方根反比衰減,則收斂僅在 50 步后變得更好。
def polynomial_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return (1 + 0.1 * t) ** (-0.5) t = 1 lr = polynomial_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: -0.060831, x2: 0.028779
def polynomial_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return (1 + 0.1 * t) ** (-0.5) t = 1 lr = polynomial_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: 0.025029, x2: 0.115820
def polynomial_lr(): # Global variable that is defined outside this function and updated inside global t t += 1 return (1 + 0.1 * t) ** (-0.5) t = 1 lr = polynomial_lr d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: 0.280001, x2: -0.037688
關于如何設置學習率,還有更多選擇。例如,我們可以從一個小的速率開始,然后迅速上升,然后再次下降,盡管速度會更慢。我們甚至可以在更小和更大的學習率之間交替。存在多種此類時間表。現在讓我們關注可以進行綜合理論分析的學習率計劃,即凸設置中的學習率。對于一般的非凸問題,很難獲得有意義的收斂保證,因為通常最小化非線性非凸問題是 NP 難題。有關調查,請參見 Tibshirani 2015 的優秀講義 。
12.4.3。凸目標的收斂性分析
以下針對凸目標函數的隨機梯度下降的收斂分析是可選的,主要用于傳達有關問題的更多直覺。我們將自己限制在最簡單的證明之一(Nesterov 和 Vial,2000)。存在顯著更高級的證明技術,例如,每當目標函數表現得特別好時。
假設目標函數 f(ξ,x)是凸的x 對全部ξ. 更具體地說,我們考慮隨機梯度下降更新:
(12.4.6)xt+1=xt?ηt?xf(ξt,x),
在哪里f(ξt,x)是關于訓練樣例的目標函數ξt 在步驟中從一些分布中提取t和x是模型參數。表示為
(12.4.7)R(x)=Eξ[f(ξ,x)]
預期的風險和R?它的最低限度 x. 最后讓x?是最小化器(我們假設它存在于x被定義為)。在這種情況下,我們可以跟蹤當前參數之間的距離xt在時間t和風險最小化 x?看看它是否隨著時間的推移而改善:
(12.4.8)‖xt+1?x?‖2=‖xt?ηt?xf(ξt,x)?x?‖2=‖xt?x?‖2+ηt2‖?xf(ξt,x)‖2?2ηt?xt?x?,?xf(ξt,x)?.
我們假設?2隨機梯度范數 ?xf(ξt,x)受一些常數的限制L, 因此我們有
(12.4.9)ηt2‖?xf(ξt,x)‖2≤ηt2L2.
我們最感興趣的是兩者之間的距離 xt和x?預期的變化。事實上,對于任何特定的步驟序列,距離很可能會增加,具體取決于哪個ξt我們遇到。因此我們需要綁定點積。因為對于任何凸函數f它認為 f(y)≥f(x)+?f′(x),y?x? 對全部x和y, 根據凸性我們有
(12.4.10)f(ξt,x?)≥f(ξt,xt)+?x??xt,?xf(ξt,xt)?.
將不等式(12.4.9)和 (12.4.10)代入(12.4.8)我們得到了時間參數之間距離的界限t+1如下:
(12.4.11)‖xt?x?‖2?‖xt+1?x?‖2≥2ηt(f(ξt,xt)?f(ξt,x?))?ηt2L2.
這意味著只要當前損失與最優損失之間的差異大于ηtL2/2. 由于這種差異必然會收斂到零,因此學習率ηt也需要消失。
接下來我們對(12.4.11)進行期望。這產生
(12.4.12)E[‖xt?x?‖2]?E[‖xt+1?x?‖2]≥2ηt[E[R(xt)]?R?]?ηt2L2.
最后一步涉及對不等式求和 t∈{1,…,T}. 由于總和望遠鏡并且通過刪除較低的項我們獲得
(12.4.13)‖x1?x?‖2≥2(∑t=1Tηt)[E[R(xt)]?R?]?L2∑t=1Tηt2.
請注意,我們利用了x1是給定的,因此可以放棄期望。最后定義
(12.4.14)xˉ=def∑t=1Tηtxt∑t=1Tηt.
自從
(12.4.15)E(∑t=1TηtR(xt)∑t=1Tηt)=∑t=1TηtE[R(xt)]∑t=1Tηt=E[R(xt)],
由 Jensen 不等式(設置i=t, αi=ηt/∑t=1Tηt在 (12.2.3) ) 和凸性R它遵循E[R(xt)]≥E[R(xˉ)], 因此
(12.4.16)∑t=1TηtE[R(xt)]≥∑t=1TηtE[R(xˉ)].
將其代入不等式(12.4.13)得到邊界
(12.4.17)[E[xˉ]]?R?≤r2+L2∑t=1Tηt22∑t=1Tηt,
在哪里 r2=def‖x1?x?‖2 是參數的初始選擇與最終結果之間距離的界限。簡而言之,收斂速度取決于隨機梯度的范數如何有界(L) 以及初始參數值離最優性有多遠 (r). 請注意,邊界是根據xˉ而不是 xT. 這是因為xˉ是優化路徑的平滑版本。每當r,L, 和 T已知我們可以選擇學習率 η=r/(LT). 這產生作為上限 rL/T. 也就是說,我們收斂于 rate O(1/T)到最優解。
12.4.4。隨機梯度和有限樣本
到目前為止,在談到隨機梯度下降時,我們玩得有點快和松了。我們假設我們繪制實例 xi,通常帶有標簽yi從一些分布 p(x,y)并且我們使用它以某種方式更新模型參數。特別地,對于有限的樣本量,我們簡單地認為離散分布 p(x,y)=1n∑i=1nδxi(x)δyi(y) 對于某些功能δxi和δyi允許我們對其執行隨機梯度下降。
然而,這并不是我們所做的。在當前部分的玩具示例中,我們只是將噪聲添加到其他非隨機梯度中,即,我們假裝有對(xi,yi). 事實證明,這是有道理的(詳細討論見習題)。更麻煩的是,在之前的所有討論中,我們顯然都沒有這樣做。相反,我們只對所有實例進行一次迭代。要了解為什么這樣做更可取,請考慮相反的情況,即我們正在抽樣n從帶有替換的離散分布觀察 。選擇元素的概率i隨機是1/n. 因此至少選擇一次是
(12.4.18)P(choosei)=1?P(omiti)=1?(1?1/n)n≈1?e?1≈0.63.
類似的推理表明,恰好一次選擇某個樣本(即訓練示例)的概率由下式給出
(12.4.19)(n1)1n(1?1n)n?1=nn?1(1?1n)n≈e?1≈0.37.
相對于無放回抽樣,放回抽樣會導致方差增加和數據效率降低。因此,在實踐中我們執行后者(這是貫穿本書的默認選擇)。最后請注意,重復通過訓練數據集以不同的隨機順序遍歷它。
12.4.5。概括
對于凸問題,我們可以證明,對于廣泛選擇的學習率,隨機梯度下降將收斂到最優解。
對于深度學習,通常情況并非如此。然而,對凸問題的分析讓我們對如何接近優化有了有用的認識,即逐步降低學習率,盡管不是太快。
學習率太小或太大時都會出現問題。在實踐中,通常需要經過多次實驗才能找到合適的學習率。
當訓練數據集中有更多示例時,梯度下降的每次迭代計算成本更高,因此在這些情況下首選隨機梯度下降。
隨機梯度下降的最優性保證在非凸情況下通常不可用,因為需要檢查的局部最小值的數量很可能是指數級的。
12.4.6。練習
試驗隨機梯度下降的不同學習率計劃和不同的迭代次數。特別是,繪制與最佳解決方案的距離 (0,0)作為迭代次數的函數。
證明對于函數f(x1,x2)=x12+2x22 向梯度添加正常噪聲相當于最小化損失函數 f(x,w)=(x1?w1)2+2(x2?w2)2 在哪里x從正態分布中提取。
當您從中采樣時比較隨機梯度下降的收斂性{(x1,y1),…,(xn,yn)}有更換和當您在沒有更換的情況下取樣時。
如果某個梯度(或者與其相關的某個坐標)始終大于所有其他梯度,您將如何更改隨機梯度下降求解器?
假使,假設f(x)=x2(1+sin?x). 有多少局部最小值f有?你能改變嗎f以這樣一種方式來最小化它需要評估所有局部最小值?
-
隨機梯度下降
+關注
關注
0文章
4瀏覽量
979 -
pytorch
+關注
關注
2文章
808瀏覽量
13310
發布評論請先 登錄
相關推薦
隨機梯度估值在盲均衡算法中的影響
機器學習:隨機梯度下降和批量梯度下降算法介紹
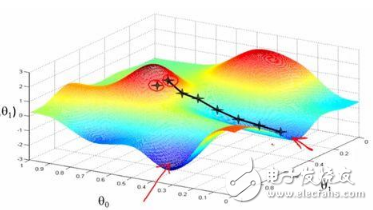
一文看懂常用的梯度下降算法
梯度下降算法及其變種:批量梯度下降,小批量梯度下降和隨機梯度下降
基于PyTorch的深度學習入門教程之PyTorch的自動梯度計算
基于PyTorch的深度學習入門教程之PyTorch重點綜合實踐
基于分布式編碼的同步隨機梯度下降算法





 PyTorch教程-12.4。隨機梯度下降
PyTorch教程-12.4。隨機梯度下降
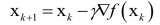











評論