到目前為止，我們主要關注如何更新權重向量的優化算法，而不是更新權重向量的速率。盡管如此，調整學習率通常與實際算法一樣重要。有幾個方面需要考慮：

最明顯的是學習率的大小很重要。如果它太大，優化就會發散，如果它太小，訓練時間太長，或者我們最終會得到一個次優的結果。我們之前看到問題的條件編號很重要（例如，參見第 12.6 節了解詳細信息）。直觀地說，它是最不敏感方向的變化量與最敏感方向的變化量之比。

其次，衰減率同樣重要。如果學習率仍然很大，我們可能最終會在最小值附近跳來跳去，因此無法達到最優。12.5 節 詳細討論了這一點，我們在12.4 節中分析了性能保證。簡而言之，我們希望速率下降，但可能比O(t?12)這將是凸問題的不錯選擇。

另一個同樣重要的方面是初始化。這既涉及參數的初始設置方式（詳見 第 5.4 節），也涉及它們最初的演變方式。這在熱身的綽號下進行，即我們最初開始朝著解決方案前進的速度。一開始的大步驟可能沒有好處，特別是因為初始參數集是隨機的。最初的更新方向也可能毫無意義。

最后，還有許多執行循環學習率調整的優化變體。這超出了本章的范圍。我們建議讀者查看 Izmailov等人的詳細信息。( 2018 )，例如，如何通過對整個參數路徑進行平均來獲得更好的解決方案。

鑒于管理學習率需要很多細節，大多數深度學習框架都有自動處理這個問題的工具。在本章中，我們將回顧不同的調度對準確性的影響，并展示如何通過學習率調度器有效地管理它。

12.11.1。玩具問題

我們從一個玩具問題開始，這個問題足夠簡單，可以輕松計算，但又足夠不平凡，可以說明一些關鍵方面。為此，我們選擇了一個稍微現代化的 LeNet 版本（relu而不是 sigmoid激活，MaxPooling 而不是 AveragePooling）應用于 Fashion-MNIST。此外，我們混合網絡以提高性能。由于大部分代碼都是標準的，我們只介紹基礎知識而不進行進一步的詳細討論。如有需要，請參閱第 7 節進行復習。

%matplotlib inline
import math
import torch
from torch import nn
from torch.optim import lr_scheduler
from d2l import torch as d2l


def net_fn():
  model = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.ReLU(),
    nn.Linear(120, 84), nn.ReLU(),
    nn.Linear(84, 10))

  return model

loss = nn.CrossEntropyLoss()
device = d2l.try_gpu()

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

# The code is almost identical to `d2l.train_ch6` defined in the
# lenet section of chapter convolutional neural networks
def train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
     scheduler=None):
  net.to(device)
  animator = d2l.Animator(xlabel='epoch', xlim=[0, num_epochs],
              legend=['train loss', 'train acc', 'test acc'])

  for epoch in range(num_epochs):
    metric = d2l.Accumulator(3) # train_loss, train_acc, num_examples
    for i, (X, y) in enumerate(train_iter):
      net.train()
      trainer.zero_grad()
      X, y = X.to(device), y.to(device)
      y_hat = net(X)
      l = loss(y_hat, y)
      l.backward()
      trainer.step()
      with torch.no_grad():
        metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
      train_loss = metric[0] / metric[2]
      train_acc = metric[1] / metric[2]
      if (i + 1) % 50 == 0:
        animator.add(epoch + i / len(train_iter),
               (train_loss, train_acc, None))

    test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
    animator.add(epoch+1, (None, None, test_acc))

    if scheduler:
      if scheduler.__module__ == lr_scheduler.__name__:
        # Using PyTorch In-Built scheduler
        scheduler.step()
      else:
        # Using custom defined scheduler
        for param_group in trainer.param_groups:
          param_group['lr'] = scheduler(epoch)

  print(f'train loss {train_loss:.3f}, train acc {train_acc:.3f}, '
     f'test acc {test_acc:.3f}')

%matplotlib inline
from mxnet import autograd, gluon, init, lr_scheduler, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l

npx.set_np()

net = nn.HybridSequential()
net.add(nn.Conv2D(channels=6, kernel_size=5, padding=2, activation='relu'),
    nn.MaxPool2D(pool_size=2, strides=2),
    nn.Conv2D(channels=16, kernel_size=5, activation='relu'),
    nn.MaxPool2D(pool_size=2, strides=2),
    nn.Dense(120, activation='relu'),
    nn.Dense(84, activation='relu'),
    nn.Dense(10))
net.hybridize()
loss = gluon.loss.SoftmaxCrossEntropyLoss()
device = d2l.try_gpu()

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

# The code is almost identical to `d2l.train_ch6` defined in the
# lenet section of chapter convolutional neural networks
def train(net, train_iter, test_iter, num_epochs, loss, trainer, device):
  net.initialize(force_reinit=True, ctx=device, init=init.Xavier())
  animator = d2l.Animator(xlabel='epoch', xlim=[0, num_epochs],
              legend=['train loss', 'train acc', 'test acc'])
  for epoch in range(num_epochs):
    metric = d2l.Accumulator(3) # train_loss, train_acc, num_examples
    for i, (X, y) in enumerate(train_iter):
      X, y = X.as_in_ctx(device), y.as_in_ctx(device)
      with autograd.record():
        y_hat = net(X)
        l = loss(y_hat, y)
      l.backward()
      trainer.step(X.shape[0])
      metric.add(l.sum(), d2l.accuracy(y_hat, y), X.shape[0])
      train_loss = metric[0] / metric[2]
      train_acc = metric[1] / metric[2]
      if (i + 1) % 50 == 0:
        animator.add(epoch + i / len(train_iter),
               (train_loss, train_acc, None))
    test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
    animator.add(epoch + 1, (None, None, test_acc))
  print(f'train loss {train_loss:.3f}, train acc {train_acc:.3f}, '
     f'test acc {test_acc:.3f}')

%matplotlib inline
import math
import tensorflow as tf
from tensorflow.keras.callbacks import LearningRateScheduler
from d2l import tensorflow as d2l


def net():
  return tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(filters=6, kernel_size=5, activation='relu',
                padding='same'),
    tf.keras.layers.AvgPool2D(pool_size=2, strides=2),
    tf.keras.layers.Conv2D(filters=16, kernel_size=5,
                activation='relu'),
    tf.keras.layers.AvgPool2D(pool_size=2, strides=2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(120, activation='relu'),
    tf.keras.layers.Dense(84, activation='sigmoid'),
    tf.keras.layers.Dense(10)])


batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

# The code is almost identical to `d2l.train_ch6` defined in the
# lenet section of chapter convolutional neural networks
def train(net_fn, train_iter, test_iter, num_epochs, lr,
       device=d2l.try_gpu(), custom_callback = False):
  device_name = device._device_name
  strategy = tf.distribute.OneDeviceStrategy(device_name)
  with strategy.scope():
    optimizer = tf.keras.optimizers.SGD(learning_rate=lr)
    loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
    net = net_fn()
    net.compile(optimizer=optimizer, loss=loss, metrics=['accuracy'])
  callback = d2l.TrainCallback(net, train_iter, test_iter, num_epochs,
               device_name)
  if custom_callback is False:
    net.fit(train_iter, epochs=num_epochs, verbose=0,
        callbacks=[callback])
  else:
     net.fit(train_iter, epochs=num_epochs, verbose=0,
         callbacks=[callback, custom_callback])
  return net

WARNING:tensorflow:From /home/d2l-worker/miniconda3/envs/d2l-en-release-1/lib/python3.9/site-packages/tensorflow/python/autograph/pyct/static_analysis/liveness.py:83: Analyzer.lamba_check (from tensorflow.python.autograph.pyct.static_analysis.liveness) is deprecated and will be removed after 2023-09-23.
Instructions for updating:
Lambda fuctions will be no more assumed to be used in the statement where they are used, or at least in the same block. https://github.com/tensorflow/tensorflow/issues/56089

讓我們看看如果我們使用默認設置調用此算法會發生什么，例如學習率為0.3并訓練 30迭代。請注意訓練準確性如何不斷提高，而測試準確性方面的進展卻停滯不前。兩條曲線之間的差距表明過度擬合。

lr, num_epochs = 0.3, 30
net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.159, train acc 0.939, test acc 0.882

lr, num_epochs = 0.3, 30
net.initialize(force_reinit=True, ctx=device, init=init.Xavier())
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.135, train acc 0.948, test acc 0.885

lr, num_epochs = 0.3, 30
train(net, train_iter, test_iter, num_epochs, lr)

loss 0.218, train acc 0.918, test acc 0.889
46772.7 examples/sec on /GPU:0

12.11.2。調度程序

調整學習率的一種方法是在每一步明確設置它。這通過該set_learning_rate方法方便地實現。我們可以在每個 epoch 之后（甚至在每個 minibatch 之后）向下調整它，例如，以動態方式響應優化的進展情況。

lr = 0.1
trainer.param_groups[0]["lr"] = lr
print(f'learning rate is now {trainer.param_groups[0]["lr"]:.2f}')

learning rate is now 0.10

trainer.set_learning_rate(0.1)
print(f'learning rate is now {trainer.learning_rate:.2f}')

learning rate is now 0.10

lr = 0.1
dummy_model = tf.keras.models.Sequential([tf.keras.layers.Dense(10)])
dummy_model.compile(tf.keras.optimizers.SGD(learning_rate=lr), loss='mse')
print(f'learning rate is now ,', dummy_model.optimizer.lr.numpy())

learning rate is now , 0.1

更一般地說，我們想要定義一個調度程序。當使用更新次數調用時，它會返回適當的學習率值。讓我們定義一個簡單的學習率設置為 η=η0(t+1)?12.

class SquareRootScheduler:
  def __init__(self, lr=0.1):
    self.lr = lr

  def __call__(self, num_update):
    return self.lr * pow(num_update + 1.0, -0.5)

class SquareRootScheduler:
  def __init__(self, lr=0.1):
    self.lr = lr

  def __call__(self, num_update):
    return self.lr * pow(num_update + 1.0, -0.5)

class SquareRootScheduler:
  def __init__(self, lr=0.1):
    self.lr = lr

  def __call__(self, num_update):
    return self.lr * pow(num_update + 1.0, -0.5)

讓我們繪制它在一系列值上的行為。

scheduler = SquareRootScheduler(lr=0.1)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

scheduler = SquareRootScheduler(lr=0.1)
d2l.plot(np.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

scheduler = SquareRootScheduler(lr=0.1)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

現在讓我們看看這對 Fashion-MNIST 的訓練有何影響。我們只是將調度程序作為訓練算法的附加參數提供。

net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
   scheduler)

train loss 0.284, train acc 0.896, test acc 0.874

trainer = gluon.Trainer(net.collect_params(), 'sgd',
            {'lr_scheduler': scheduler})
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.524, train acc 0.810, test acc 0.812

train(net, train_iter, test_iter, num_epochs, lr,
   custom_callback=LearningRateScheduler(scheduler))

loss 0.381, train acc 0.860, test acc 0.848
49349.5 examples/sec on /GPU:0

這比以前好很多。有兩點很突出：曲線比以前更平滑。其次，過度擬合較少。不幸的是，關于為什么某些策略在理論上會導致較少的過度擬合，這并不是一個很好解決的問題。有人認為較小的步長會導致參數更接近于零，從而更簡單。然而，這并不能完全解釋這種現象，因為我們并沒有真正提前停止，而只是輕輕地降低學習率。

12.11.3。政策

雖然我們不可能涵蓋所有種類的學習率調度器，但我們嘗試在下面簡要概述流行的策略。常見的選擇是多項式衰減和分段常數計劃。除此之外，已發現余弦學習率計劃在某些問題上憑經驗表現良好。最后，在某些問題上，在使用大學習率之前預熱優化器是有益的。

12.11.3.1。因子調度器

多項式衰減的一種替代方法是乘法衰減，即ηt+1←ηt?α為了 α∈(0,1). 為了防止學習率衰減超過合理的下限，更新方程通常被修改為 ηt+1←max?(ηmin,ηt?α).

class FactorScheduler:
  def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):
    self.factor = factor
    self.stop_factor_lr = stop_factor_lr
    self.base_lr = base_lr

  def __call__(self, num_update):
    self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)
    return self.base_lr

scheduler = FactorScheduler(factor=0.9, stop_factor_lr=1e-2, base_lr=2.0)
d2l.plot(torch.arange(50), [scheduler(t) for t in range(50)])

class FactorScheduler:
  def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):
    self.factor = factor
    self.stop_factor_lr = stop_factor_lr
    self.base_lr = base_lr

  def __call__(self, num_update):
    self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)
    return self.base_lr

scheduler = FactorScheduler(factor=0.9, stop_factor_lr=1e-2, base_lr=2.0)
d2l.plot(np.arange(50), [scheduler(t) for t in range(50)])

class FactorScheduler:
  def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):
    self.factor = factor
    self.stop_factor_lr = stop_factor_lr
    self.base_lr = base_lr

  def __call__(self, num_update):
    self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)
    return self.base_lr

scheduler = FactorScheduler(factor=0.9, stop_factor_lr=1e-2, base_lr=2.0)
d2l.plot(tf.range(50), [scheduler(t) for t in range(50)])

這也可以通過 MXNet 中的內置調度程序通過 lr_scheduler.FactorScheduler對象來完成。它需要更多的參數，例如預熱周期、預熱模式（線性或恒定）、所需更新的最大數量等；展望未來，我們將酌情使用內置調度程序，并僅在此處解釋它們的功能。如圖所示，如果需要，構建您自己的調度程序相當簡單。

12.11.3.2。多因素調度程序

訓練深度網絡的一個常見策略是保持學習率分段不變，并每隔一段時間將其降低一個給定的數量。也就是說，給定一組降低速率的時間，例如 s={5,10,20}減少 ηt+1←ηt?α每當 t∈s. 假設值在每一步都減半，我們可以按如下方式實現。

net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
scheduler = lr_scheduler.MultiStepLR(trainer, milestones=[15, 30], gamma=0.5)

def get_lr(trainer, scheduler):
  lr = scheduler.get_last_lr()[0]
  trainer.step()
  scheduler.step()
  return lr

d2l.plot(torch.arange(num_epochs), [get_lr(trainer, scheduler)
                 for t in range(num_epochs)])

scheduler = lr_scheduler.MultiFactorScheduler(step=[15, 30], factor=0.5,
                       base_lr=0.5)
d2l.plot(np.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

class MultiFactorScheduler:
  def __init__(self, step, factor, base_lr):
    self.step = step
    self.factor = factor
    self.base_lr = base_lr

  def __call__(self, epoch):
    if epoch in self.step:
      self.base_lr = self.base_lr * self.factor
      return self.base_lr
    else:
      return self.base_lr

scheduler = MultiFactorScheduler(step=[15, 30], factor=0.5, base_lr=0.5)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

這種分段恒定學習率計劃背后的直覺是，讓優化繼續進行，直到根據權重向量的分布達到穩定點。然后（也只有那時）我們會降低速率以獲得更高質量的代理到良好的局部最小值。下面的例子展示了這如何產生更好的解決方案。

train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
   scheduler)

train loss 0.186, train acc 0.931, test acc 0.897

trainer = gluon.Trainer(net.collect_params(), 'sgd',
            {'lr_scheduler': scheduler})
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.195, train acc 0.926, test acc 0.893

train(net, train_iter, test_iter, num_epochs, lr,
   custom_callback=LearningRateScheduler(scheduler))

loss 0.237, train acc 0.913, test acc 0.882
49476.3 examples/sec on /GPU:0

12.11.3.3。余弦調度程序

Loshchilov 和 Hutter ( 2016 )提出了一種相當令人費解的啟發式方法 。它依賴于這樣的觀察，即我們可能不想在開始時過分降低學習率，而且我們可能希望最終使用非常小的學習率來“完善”解決方案。這導致類似余弦的時間表具有以下范圍內學習率的函數形式t∈[0,T].

(12.11.1)ηt=ηT+η0?ηT2(1+cos?(πt/T))

這里η0是初始學習率，ηT是當時的目標利率T. 此外，對于t>T我們只需將值固定到ηT無需再次增加。在下面的例子中，我們設置最大更新步長T=20.

class CosineScheduler:
  def __init__(self, max_update, base_lr=0.01, final_lr=0,
        warmup_steps=0, warmup_begin_lr=0):
    self.base_lr_orig = base_lr
    self.max_update = max_update
    self.final_lr = final_lr
    self.warmup_steps = warmup_steps
    self.warmup_begin_lr = warmup_begin_lr
    self.max_steps = self.max_update - self.warmup_steps

  def get_warmup_lr(self, epoch):
    increase = (self.base_lr_orig - self.warmup_begin_lr) 
            * float(epoch) / float(self.warmup_steps)
    return self.warmup_begin_lr + increase

  def __call__(self, epoch):
    if epoch < self.warmup_steps:
      return self.get_warmup_lr(epoch)
    if epoch <= self.max_update:
      self.base_lr = self.final_lr + (
        self.base_lr_orig - self.final_lr) * (1 + math.cos(
        math.pi * (epoch - self.warmup_steps) / self.max_steps)) / 2
    return self.base_lr

scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

scheduler = lr_scheduler.CosineScheduler(max_update=20, base_lr=0.3,
                     final_lr=0.01)
d2l.plot(np.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

class CosineScheduler:
  def __init__(self, max_update, base_lr=0.01, final_lr=0,
        warmup_steps=0, warmup_begin_lr=0):
    self.base_lr_orig = base_lr
    self.max_update = max_update
    self.final_lr = final_lr
    self.warmup_steps = warmup_steps
    self.warmup_begin_lr = warmup_begin_lr
    self.max_steps = self.max_update - self.warmup_steps

  def get_warmup_lr(self, epoch):
    increase = (self.base_lr_orig - self.warmup_begin_lr) 
            * float(epoch) / float(self.warmup_steps)
    return self.warmup_begin_lr + increase

  def __call__(self, epoch):
    if epoch < self.warmup_steps:
      return self.get_warmup_lr(epoch)
    if epoch <= self.max_update:
      self.base_lr = self.final_lr + (
        self.base_lr_orig - self.final_lr) * (1 + math.cos(
        math.pi * (epoch - self.warmup_steps) / self.max_steps)) / 2
    return self.base_lr

scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

在計算機視覺的背景下，這個時間表可以帶來更好的結果。但請注意，不能保證此類改進（如下所示）。

net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=0.3)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
   scheduler)

train loss 0.229, train acc 0.916, test acc 0.886

trainer = gluon.Trainer(net.collect_params(), 'sgd',
            {'lr_scheduler': scheduler})
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.345, train acc 0.876, test acc 0.866

train(net, train_iter, test_iter, num_epochs, lr,
   custom_callback=LearningRateScheduler(scheduler))

loss 0.261, train acc 0.905, test acc 0.881
49572.1 examples/sec on /GPU:0

12.11.3.4。暖身

在某些情況下，初始化參數不足以保證獲得良好的解決方案。對于一些可能導致不穩定的優化問題的高級網絡設計來說，這尤其是一個問題。我們可以通過選擇足夠小的學習率來解決這個問題，以防止在開始時出現分歧。不幸的是，這意味著進展緩慢。相反，較大的學習率最初會導致發散。

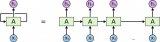
解決這個難題的一個相當簡單的方法是使用一個預熱期，在此期間學習率增加到其初始最大值，并降低學習率直到優化過程結束。為簡單起見，通常為此目的使用線性增加。這導致了如下所示表格的時間表。

scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

scheduler = lr_scheduler.CosineScheduler(20, warmup_steps=5, base_lr=0.3,
                     final_lr=0.01)
d2l.plot(np.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)
d2l.plot(tf.range(num_epochs), [scheduler(t) for t in range(num_epochs)])

請注意，網絡最初收斂得更好（特別是觀察前 5 個時期的表現）。

net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=0.3)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
   scheduler)

train loss 0.173, train acc 0.936, test acc 0.902

trainer = gluon.Trainer(net.collect_params(), 'sgd',
            {'lr_scheduler': scheduler})
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

train loss 0.347, train acc 0.875, test acc 0.871

train(net, train_iter, test_iter, num_epochs, lr,
   custom_callback=LearningRateScheduler(scheduler))

loss 0.270, train acc 0.901, test acc 0.880
49891.2 examples/sec on /GPU:0

預熱可以應用于任何調度程序（不僅僅是余弦）。有關學習率計劃和更多實驗的更詳細討論，另請參閱（Gotmare等人，2018 年）。特別是，他們發現預熱階段限制了非常深的網絡中參數的發散量。這在直覺上是有道理的，因為我們預計由于網絡中那些在開始時花費最多時間取得進展的部分的隨機初始化會出現顯著差異。

12.11.4。概括

在訓練期間降低學習率可以提高準確性并（最令人費解的是）減少模型的過度擬合。

每當進展趨于平穩時，學習率的分段降低在實踐中是有效的。從本質上講，這可以確保我們有效地收斂到一個合適的解決方案，然后才通過降低學習率來減少參數的固有方差。

余弦調度器在某些計算機視覺問題上很受歡迎。有關此類調度程序的詳細信息，請參見例如GluonCV 。

優化前的預熱期可以防止發散。

優化在深度學習中有多種用途。除了最小化訓練目標外，優化算法和學習率調度的不同選擇可能導致測試集上的泛化和過度擬合量大不相同（對于相同數量的訓練誤差）。

12.11.5。練習

試驗給定固定學習率的優化行為。您可以通過這種方式獲得的最佳模型是什么？

如果改變學習率下降的指數，收斂性會如何變化？PolyScheduler為了方便您在實驗中使用。

將余弦調度程序應用于大型計算機視覺問題，例如訓練 ImageNet。相對于其他調度程序，它如何影響性能？

熱身應該持續多長時間？

你能把優化和抽樣聯系起來嗎？首先使用Welling 和 Teh ( 2011 )關于隨機梯度朗之萬動力學的結果。