即使在中等規模的數據集上,訓練神經網絡也可能很昂貴。根據配置空間(第 19.1.1.2 節),超參數優化需要數十到數百次函數評估才能找到性能良好的超參數配置。正如我們在19.3 節中看到的 ,我們可以通過利用并行資源顯著加快 HPO 的整體時鐘時間,但這并不會減少所需的總計算量。
在本節中,我們將展示如何加速超參數配置的評估。隨機搜索等方法為每個超參數評估分配相同數量的資源(例如,epoch 數、訓練數據點)。圖 19.4.1 描繪了一組使用不同超參數配置訓練的神經網絡的學習曲線。經過幾個 epoch 之后,我們已經能夠在視覺上區分性能良好和次優的配置。然而,學習曲線是嘈雜的,我們可能仍然需要全部 100 個 epoch 來確定表現最好的一個。
圖 19.4.1隨機超參數配置的學習曲線
多保真超參數優化將更多資源分配給有前途的配置,并盡早停止對性能不佳的配置的評估。這加快了優化過程,因為我們可以為相同的資源總量嘗試更多的配置。
更正式地說,我們擴展了第 19.1.1 節中的定義 ,這樣我們的目標函數 f(x,r)獲得額外的輸入 r∈[rmin,rmax], 指定我們愿意為配置評估花費的資源量x. 我們假設錯誤 f(x,r)隨著r,而計算成本c(x,r)增加。通常, r表示訓練神經網絡的時期數,但它也可以是訓練子集大小或交叉驗證折疊數。
from collections import defaultdict import numpy as np from scipy import stats from d2l import torch as d2l d2l.set_figsize()
19.4.1。連續減半
使隨機搜索適應多保真度設置的最簡單方法之一是連續減半 (Jamieson 和 Talwalkar,2016 年,Karnin等人,2013 年)。基本思想是從N配置,例如從配置空間隨機采樣,并訓練它們中的每一個 rmin只有時代。然后,我們丟棄一部分表現最差的試驗,并對其余試驗進行更長時間的訓練。重復這個過程,更少的試驗運行更長時間,直到至少有一個試驗達到rmax時代。
更正式地說,考慮最低預算rmin(例如 1 個 epoch),最大預算rmax,例如 max_epochs在我們之前的例子中,還有一個減半常數 η∈{2,3,…}. 為簡單起見,假設 rmax=rminηK, 和K∈I. 那么初始配置的數量是N=ηK. 讓我們定義一組梯級 R={rmin,rminη,rminη2,…,rmax}.
一輪連續減半的過程如下。我們從跑步開始N試驗到第一梯級rmin. 對驗證錯誤進行排序,我們保持頂部1/η分數(相當于ηK?1配置)并丟棄所有其余的。幸存的試驗被訓練用于下一個梯級(rminηepochs),然后重復該過程。在每個梯級,一個1/η部分試驗存活下來,他們的訓練繼續進行η倍大的預算。有了這個特別的選擇N, 只有一個試驗將被訓練到全部預算rmax. 一旦這樣一輪連續的減半完成,我們就會用一組新的初始配置開始下一輪,迭代直到總預算用完。
圖 19.4.2隨機超參數配置的學習曲線。
我們將第 19.2 節HPOScheduler的基類子類化 ,以實現連續減半,允許通用 對象對配置進行采樣(在我們下面的示例中,它將是 a )。此外,用戶必須通過最少的資源HPOSearcherRandomSearcherrmin, 最大資源 rmax和η作為輸入。在我們的調度程序中,我們維護一個配置隊列,這些配置仍需要針對當前梯級進行評估ri. 每次我們跳到下一個梯級時,我們都會更新隊列。
class SuccessiveHalvingScheduler(d2l.HPOScheduler): #@save def __init__(self, searcher, eta, r_min, r_max, prefact=1): self.save_hyperparameters() # Compute K, which is later used to determine the number of configurations self.K = int(np.log(r_max / r_min) / np.log(eta)) # Define the rungs self.rung_levels = [r_min * eta ** k for k in range(self.K + 1)] if r_max not in self.rung_levels: # The final rung should be r_max self.rung_levels.append(r_max) self.K += 1 # Bookkeeping self.observed_error_at_rungs = defaultdict(list) self.all_observed_error_at_rungs = defaultdict(list) # Our processing queue self.queue = []
一開始我們的隊列是空的,我們用 n=prefact?ηK配置,首先在最小的梯級上進行評估rmin. 這里, prefact允許我們在不同的上下文中重用我們的代碼。出于本節的目的,我們固定 prefact=1. 每次資源可用并且HPOTuner對象查詢suggest函數時,我們都會從隊列中返回一個元素。一旦我們完成一輪連續減半,這意味著我們評估了最高資源級別上的所有幸存配置rmax并且我們的隊列是空的,我們用一組新的、隨機采樣的配置重新開始整個過程??。
@d2l.add_to_class(SuccessiveHalvingScheduler) #@save def suggest(self): if len(self.queue) == 0: # Start a new round of successive halving # Number of configurations for the first rung: n0 = int(self.prefact * self.eta ** self.K) for _ in range(n0): config = self.searcher.sample_configuration() config["max_epochs"] = self.r_min # Set r = r_min self.queue.append(config) # Return an element from the queue return self.queue.pop()
當我們收集到一個新的數據點時,我們首先更新搜索器模塊。之后我們檢查我們是否已經收集了當前梯級上的所有數據點。如果是這樣,我們對所有配置進行排序并推頂 1η配置到隊列中。
@d2l.add_to_class(SuccessiveHalvingScheduler) #@save
def update(self, config: dict, error: float, info=None):
ri = int(config["max_epochs"]) # Rung r_i
# Update our searcher, e.g if we use Bayesian optimization later
self.searcher.update(config, error, additional_info=info)
self.all_observed_error_at_rungs[ri].append((config, error))
if ri < self.r_max:
# Bookkeeping
self.observed_error_at_rungs[ri].append((config, error))
# Determine how many configurations should be evaluated on this rung
ki = self.K - self.rung_levels.index(ri)
ni = int(self.prefact * self.eta ** ki)
# If we observed all configuration on this rung r_i, we estimate the
# top 1 / eta configuration, add them to queue and promote them for
# the next rung r_{i+1}
if len(self.observed_error_at_rungs[ri]) >= ni:
kiplus1 = ki - 1
niplus1 = int(self.prefact * self.eta ** kiplus1)
best_performing_configurations = self.get_top_n_configurations(
rung_level=ri, n=niplus1
)
riplus1 = self.rung_levels[self.K - kiplus1] # r_{i+1}
# Queue may not be empty: insert new entries at the beginning
self.queue = [
dict(config, max_epochs=riplus1)
for config in best_performing_configurations
] + self.queue
self.observed_error_at_rungs[ri] = [] # Reset
配置根據其在當前梯級上觀察到的性能進行排序。
@d2l.add_to_class(SuccessiveHalvingScheduler) #@save
def get_top_n_configurations(self, rung_level, n):
rung = self.observed_error_at_rungs[rung_level]
if not rung:
return []
sorted_rung = sorted(rung, key=lambda x: x[1])
return [x[0] for x in sorted_rung[:n]]
讓我們看看在我們的神經網絡示例中連續減半是如何進行的。我們將使用rmin=2,η=2, rmax=10, 所以梯級是2,4,8,10.
min_number_of_epochs = 2 max_number_of_epochs = 10 eta = 2 num_gpus=1 config_space = { "learning_rate": stats.loguniform(1e-2, 1), "batch_size": stats.randint(32, 256), } initial_config = { "learning_rate": 0.1, "batch_size": 128, }
我們只是用新的 SuccessiveHalvingScheduler.
searcher = d2l.RandomSearcher(config_space, initial_config=initial_config) scheduler = SuccessiveHalvingScheduler( searcher=searcher, eta=eta, r_min=min_number_of_epochs, r_max=max_number_of_epochs, ) tuner = d2l.HPOTuner( scheduler=scheduler, objective=d2l.hpo_objective_lenet, ) tuner.run(number_of_trials=30)
error = 0.1623382568359375, runtime = 84.38501596450806
我們可以可視化我們評估的所有配置的學習曲線。大多數配置會提前停止,只有性能較好的配置會存活到rmax. 將此與香草隨機搜索進行比較,后者將分配rmax到每個配置。
for rung_index, rung in scheduler.all_observed_error_at_rungs.items():
errors = [xi[1] for xi in rung]
d2l.plt.scatter([rung_index] * len(errors), errors)
d2l.plt.xlim(min_number_of_epochs - 0.5, max_number_of_epochs + 0.5)
d2l.plt.xticks(
np.arange(min_number_of_epochs, max_number_of_epochs + 1),
np.arange(min_number_of_epochs, max_number_of_epochs + 1)
)
d2l.plt.ylabel("validation error")
d2l.plt.xlabel("epochs")
Text(0.5, 0, 'epochs')
最后,請注意我們在 SuccessiveHalvingScheduler. 假設一名工人可以自由運行一項工作,并suggest在當前梯級幾乎完全填滿時被調用,但另一名工人仍在忙于評估。由于我們缺少來自該工作人員的指標值,因此我們無法確定排名靠前的1/η分數打開下一個梯級。另一方面,我們想給我們的自由工人分配一份工作,這樣它就不會閑著。我們的解決方案是開始新一輪的連續減半,并??將我們的工人分配到那里的第一次試驗。然而,一旦梯級在 中完成update,我們確保在隊列的開頭插入新配置,因此它們優先于下一輪的配置。
19.4.2。概括
在本節中,我們介紹了多保真超參數優化的概念,我們假設可以訪問目標函數的廉價評估近似值,例如在一定數量的訓練時期后的驗證錯誤作為驗證錯誤的代理在全部的紀元之后。多保真超參數優化允許減少 HPO 的整體計算,而不僅僅是減少掛鐘時間。
我們實施并評估了連續減半,這是一種簡單而高效的多保真 HPO 算法。
Discussions
-
保真
+關注
關注
0文章
4瀏覽量
13596 -
pytorch
+關注
關注
2文章
808瀏覽量
13283
發布評論請先 登錄
相關推薦
Pytorch模型訓練實用PDF教程【中文】
pytorch模型轉換需要注意的事項有哪些?
基于PyTorch的深度學習入門教程之DataParallel使用多GPU
如何使用PyTorch建立網絡模型
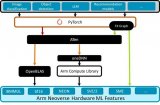
利用Arm Kleidi技術實現PyTorch優化




 PyTorch教程-19.4. 多保真超參數優化
PyTorch教程-19.4. 多保真超參數優化











評論