3D曲面重建之移動最小二乘法
本文我們思考這樣一個問題：如何在一組逐點值的給定域上估計該域的一般函數？這種估計對于給定域上PDE數值的求解，根據掃描數據進行表面重建，或者理解采集到數據的數據結構都有所幫助。下面介紹幾種常見的最小二乘法：
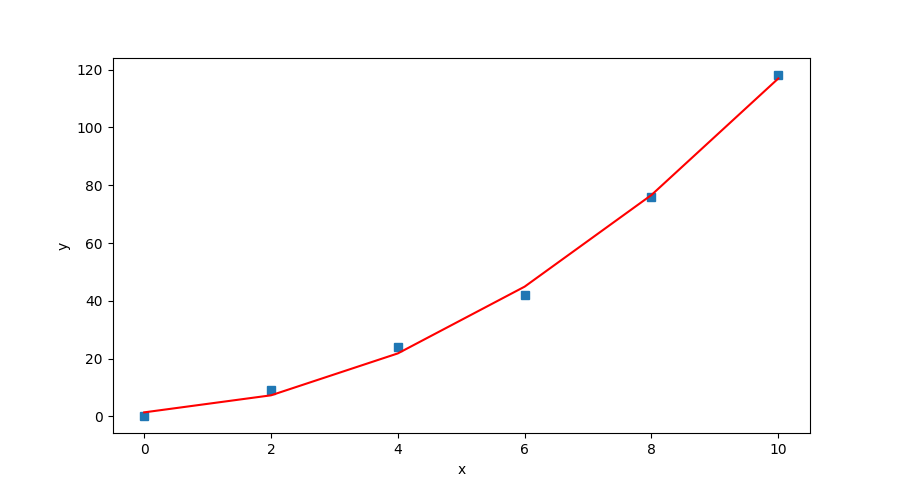
一、全局最小二乘估計
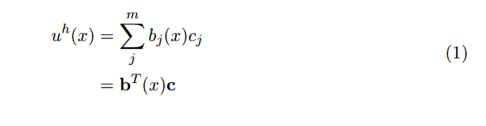
為了解決多項式擬合中的未知系數，我們構建如下的目標函數：
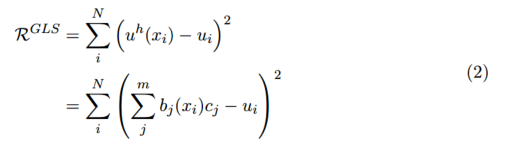
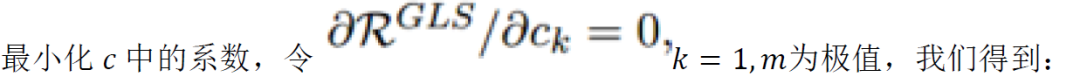
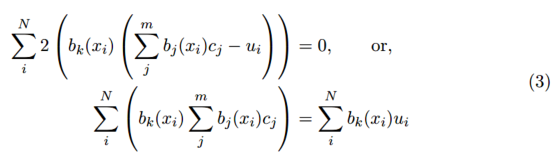
然后我們可以寫個歸一化方程為：
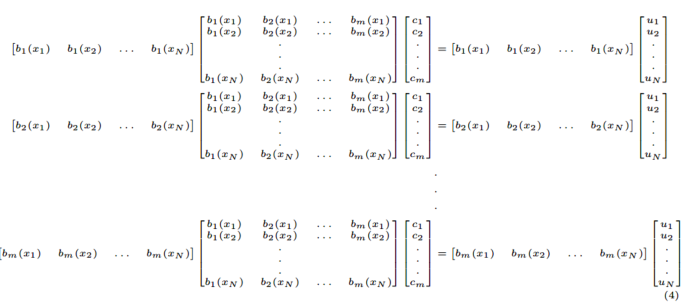
用矩陣的形式表示為：
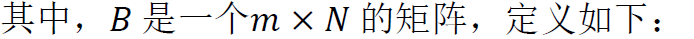
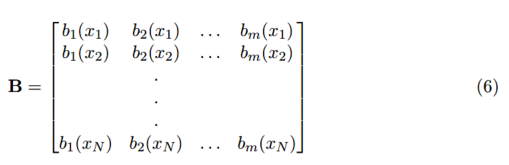
這個矩陣方程也可以直接用于計算系數向量 ：
或者在大型系統中使用迭代的方法。
或者在大型系統中使用迭代的方法。
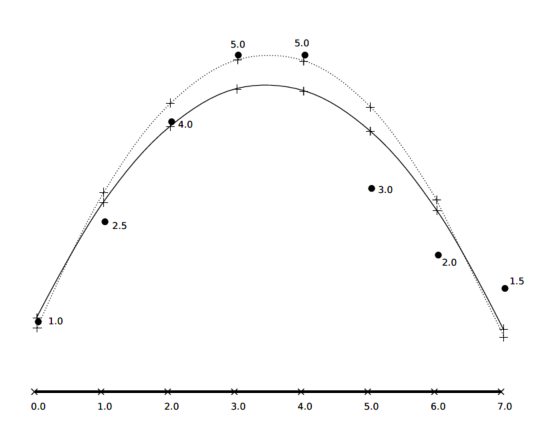
圖1 全局最小二乘（實曲線）
二、全局加權最小二乘擬合
我們可以為每個數據值分配一個權重用于最小二乘擬合中，這樣我們將目標函數最小化為：
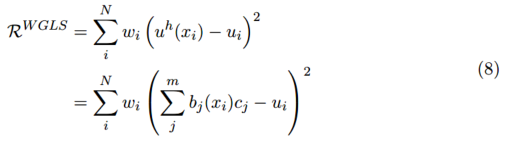
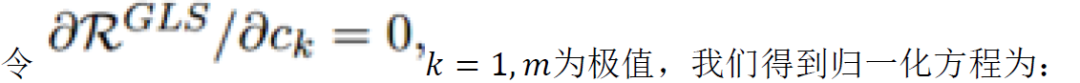
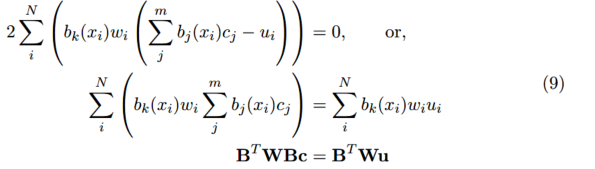
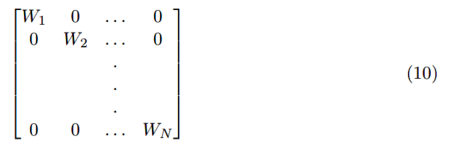
歸一化方程的解為：
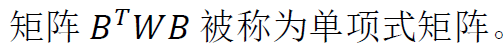
三、加權局部最小二乘
在全局最小二乘擬合中，我們假設整個域中都可以用一個單一的多項式精確地描述數據所代表的函數。但是，對于大型、復雜的數據集，這將要求我們擬合出一個不理想的高階多項式，即便如此，這也不能捕獲數據的所有特征。所以，為了替代全局解決方案，我們嘗試通過對每個數據點 及其鄰域擬合出一個低階多項式來獲得更好的解決方案。因此，有 個最小二乘擬合的值 ，每個值都是點 的近似值并且每個點的系數向量 都不同。注意：不同于其它討論的方法，這不是一種公認的方法并且也不常見。它僅僅是為了我們更好的理解下一部分將要介紹的移動最小二乘法。
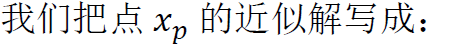
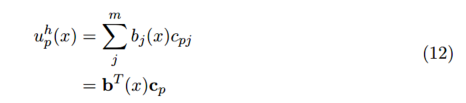
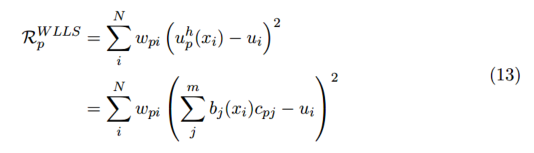
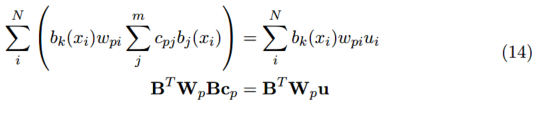
用通用的方法就可解決。
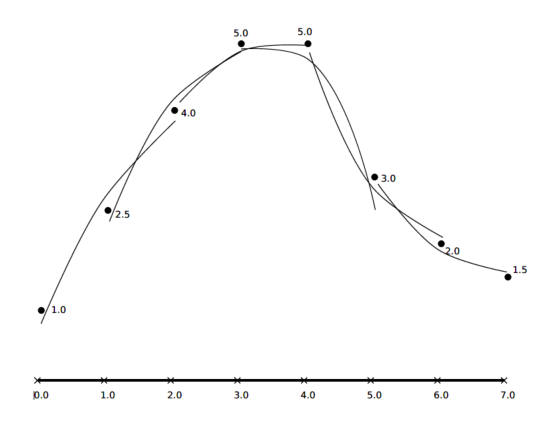
圖2 加權局部最小二乘擬合
四、移動最小二乘法
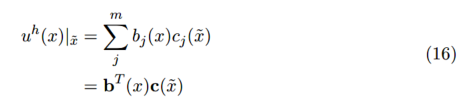
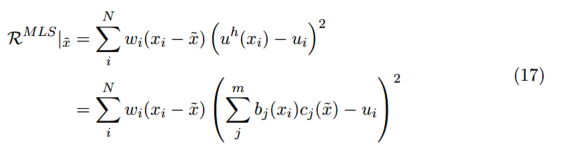
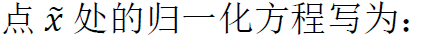
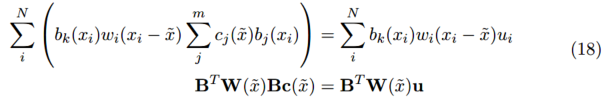
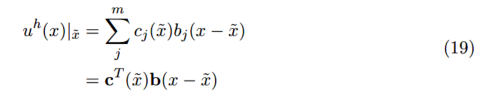
總結
聲明：本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人，不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用，如有內容侵權或者其他違規問題，請聯系本站處理。
舉報投訴
-
3D
+關注
關注
9文章
2887瀏覽量
107626 -
函數
+關注
關注
3文章
4333瀏覽量
62723 -
PDE
+關注
關注
0文章
4瀏覽量
8333
原文標題：3D曲面重建之移動最小二乘法
文章出處：【微信號：3D視覺工坊，微信公眾號：3D視覺工坊】歡迎添加關注！文章轉載請注明出處。
發布評論請先 登錄
相關推薦
講講遞推最小二乘法是什么
，正好沉浸下來，好好填填坑吧。1、遞推最小二乘法最小二乘法最早由高斯在形體運動軌道報告研究工作中提出，此后稱為參數辨識理論的基石，被廣泛應用于系統辨識和參數估計之中，不得不感嘆數學家們的偉大，工程技術
發表于 08-27 07:15
淺析遞推最小二乘法
，正好沉浸下來，好好填填坑吧。1、遞推最小二乘法最小二乘法最早由高斯在形體運動軌道報告研究工作中提出，此后稱為參數辨識理論的基石，被廣泛應用于系統辨識和參數估計之中，不得不感嘆數學家們的偉大，工程技術
發表于 08-27 06:20
遞歸最小二乘法
一、遞歸最小二乘法遞推最小二乘法：當矩陣維數增加時，矩陣求逆運算計算量過大，而且不適合在線辨識。為了減少計算量，并且可以實時地辨識出動態系統的特性，可以將最小二乘法轉換成參數遞推的估計。取前N組數據
發表于 08-27 07:03
最小二乘法的原理是什么
在嵌入式的測量中可能存在某些無法被直接測量的變量，但可能可以通過幾個不同的數據指標運算處理得到，這里介紹最小而成發，最小二乘法適用于描述Y = AX + B的數據，即尋找到最合適的一條通過X描述Y
發表于 01-11 07:05
Python實現最小二乘法是什么
最小二乘法相關知識，我把他分解成了四篇文章，第一篇是推導過 程 ，第二篇是 系數求解 ，第三篇是C語言實現二乘法（二次曲線）。
工商網監
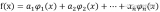
評論