好看的小说完本推荐,完美世界小说下载,完美世界txt下载

1、概念介紹

為了有效地優化代碼，編譯器需要在程序的各個節點建立并求解與信息有關的方程來收集數據流信息，并將這些信息分發給流程圖的每個塊，這個過程被稱為數據流分析。

通過檢查程序的一部分（基本程序塊），編譯器可以執行一些優化。如下圖所示：

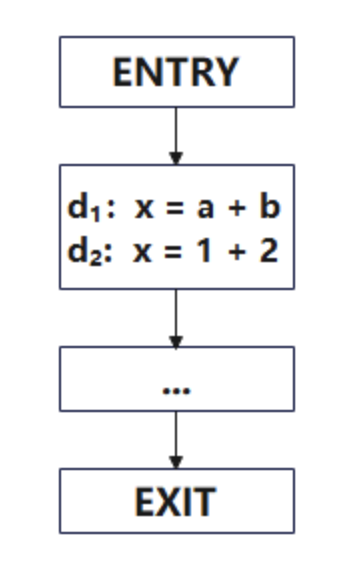
在此程序中, d1是無用的，d1中x的值永遠不會在程序中被使用；
在編譯時，d2中的表達式(1 + 2)將被計算；

所以該基本程序塊可以被優化為：x = 3。

但是有一些優化必須通過檢查整個程序來實現。如下圖所示：

從圖中可以看出：d3對c的初始化賦值是無用的，x的值恒定為6，d6可以簡化為：c = 7。

從上面這個例子可以看出，僅通過一兩個連續語句，編譯器無法發現這些優化信息。必須通過更加全面的數據流分析，以便編譯器在程序的每個節點都了解以下內容：

保證哪些變量具有恒定值
重新定義之前將使用哪些變量

這篇文章將會介紹一種數據流分析方法——區域分析，在正式開始之前，我們先來了解幾個概念：

嚴格支配：如果不首先通過x就不可能到達w，則稱x嚴格支配w。
支配：如果x嚴格支配w或x=w，則稱x支配w。

以下圖為例，如果想要到達2、3或4，必須要先通過1，所以在{1,2,3,4}集合中1占支配地位，1嚴格支配集合{2,3,4}。

流圖的區域是節點N和控制流邊E的集合，必須滿足以下條件：

N中存在一個節點頭h，它支配了N中的所有節點。
如果存在節點m可以在不經過節點頭h的情況下到達N中的節點n，則m也必然在N中。
E是N中節點之間所有控制流邊的集合，進入h的循環邊可以不包含在內。

以下圖為例，節點B1、B2、B3和B4都可以單獨看做一個區域（圖(a)）；節點B1和B2以及邊B1->B2和循環邊B2->B1組成的循環也是一個區域（圖(b)）；根據區域的第三個條件，循環邊可以不包含在區域內，所以節點B1和B2以及邊B1->B2也可以形成一個區域（圖(c)）。

然而，圖(d)中節點B3、B4以及邊B3->B4組成的子圖（虛線部分）不形成區域，因為控制流既可以通過節點B3處進入子圖，也可以通過節點B4進入子圖。B3和B4都無法做到完全支配另一個，不符合區域的第一個條件。即使我們選擇B3作為頭h，也不符合區域的第二個條件。因為B1可以不經過B3，沿著邊B1->B4到達B4，根據區域的第二個條件，B1應該在該“區域”中，但這顯然不正確。

2、區域分析的基本思想

對于每個區域R，以及R中的每個子區域R'，我們計算一個傳遞函數，該函數總結了從區域R開始到基本塊B結束執行所有可能路徑的效果。
如果基本塊B是區域R的出口塊（即區域R內的基本塊B有到R外的某個塊的傳出邊），計算區域R的每個出口塊B的傳遞函數就是計算從區域R的入口通向B過程中，執行所有可能路徑的效果，即整個區域R的傳遞函數。
從單個基本塊組成的區域開始，逐步構造更大的區域，計算更大區域的傳遞函數。
在構造更大的上層區域時，如果區域R的邊在R的上層區域上形成一個非循環流圖。我們可以繼續按上層區域的拓撲順序計算傳遞函數。
如果R是一個循環區域，那么我們只需要考慮循環邊對R入口節點的影響。
直到整個程序組成一個區域，并計算整個程序組成的區域P的傳遞函數，若入口節點處的初始值為V，則：

3、傳遞函數

在一個語句之前和之后的數據流值受該語句的語義約束，即語句前后的程序點的數據流值受該語句語義的約束，這種約束關系稱為傳遞函數。基本塊的傳遞函數表示為（以下都以Reaching Definitions 為例）：F(x) = Gen U (x - Kill)

其中，x表示基本塊B的輸入；F(x)表示基本塊B的輸出；kill表示被基本塊B中各語句殺死的變量的集合；Gen表示基本塊中沒有被各語句殺死的定值的集合。

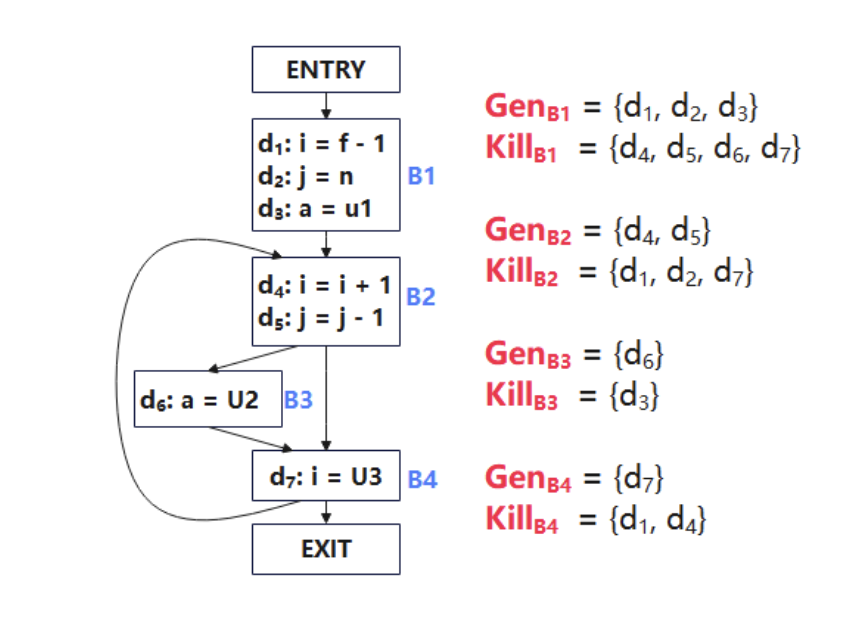
上圖顯示了流圖中各基本塊的Gen和Kill集合。以基本塊B1為例，該基本塊有三條語句：

d1: i = f-1，“生成”了一個對變量i的賦值d1，并“殺死”了程序中其它對i的賦值，即d4和d7；
d2: j = n，“生成”了一個對變量j的賦值d2，并“殺死”了程序中其它對j的賦值，即d5；
d3: a = u1，“生成”了一個對變量a的賦值d3，并“殺死”了程序中其它對a的賦值，即d6。

所以基本塊B1的Gen為{d1,d2,d3}，kill為{d4,d5,d6,d7}。

對于區域分析，構造更大的區域實際上就是更新了Gen和Kill集合的值。

4、關于傳遞函數的必要假設

為了使區域分析發揮作用，我們需要對區域中傳遞函數集的屬性做出某些假設。具體來說，我們需要對傳遞函數進行三個基本操作：組合、匯聚和閉包。

4.1 組合（composition）

節點序列的傳遞函數可以通過各個節點的傳遞函數的組合來導出。設F1和F2是兩個節點的傳遞函數，執行F1后執行F2的效果用F2(F1(x))表示：

4.2 匯聚（meet）

匯聚用于導出執行路徑不同，但輸入端點與輸出端點相同的節點。一般用F1(x)∧F2(x)表示：

4.3 閉包（closure）

如果F表示循環的傳遞函數，那么Fn表示循環n次的效果。在迭代次數未知的情況下，我們必須假設循環可以執行0次或多次。我們用F*(x)表示這樣一個循環的傳遞函數，則F的閉包如下圖所示：

5、處理可簡化流圖

可簡化流圖是指那些可以通過以下兩個規則轉換簡化為單個節點的流圖：

T1：刪除循環。如果n是具有循環的節點，即邊n->n，刪除該邊（n的所有此類邊）。

如上圖所示：R是執行T1規則后形成的新區域，原區域n的頭結點H也是新區域R的頭結點，n中H到每一個基本塊B的傳遞函數為Fn,B，則在新區域R中的傳遞函數為：

T2：刪除頂點

如果有一個節點n具有唯一的前置節點m，則將m和n合并[2]。

如上圖所示：R是執行T2規則后形成的新區域，對于n中的基本塊B，傳遞函數未改變（FR,B = Fn,B）；對于m中的基本塊：

為了構建區域的層次結構，我們需要識別循環。在可簡化流圖中（這里，我們假設流程圖都是可簡化的），任何兩個循環要么是不相交的，要么一個嵌套在另一個循環中。可簡化流圖解析到循環層次結構時，先將每個基本塊本身作為一個區域。我們將這些區域稱為葉區域。然后，從里到外排序循環，即從最里面的循環開始。處理循環時，我們通過兩個步驟將整個循環替換為一個節點：

將循環L的主體（除報頭的循環邊外的所有節點和邊）替換為代表區域R的節點。L報頭的邊現在并入R的節點。循環L的任何出口的邊被R到同一目的節點的邊替換。但是，如果控制流邊是循環邊，那么它就會成為R上的循環邊。我們稱R為主體區域。
構造一個代表整個循環L的區域R'。我們可以把R'稱作循環區域。R和R'之間唯一的區別是，后者包括循環L的循環邊。換句話說，當R'替換流圖中的R時，我們所要做的就是將R的循環邊刪除[3]。

通過重復上述操作，我們可以逐漸將大的循環減少到單個節點。由于可簡化流圖的循環是嵌套的或不相交的，因此循環區域的節點可以表示在此簡化過程中構建的一系列流圖中循環的所有節點。

最終，所有循環都被簡化為單個節點。此時，流程圖有兩種情況：一是簡化為單個節點；二是有幾個節點剩余，具有HO循環（即，簡化的流圖是多個節點的非循環圖）。在前一種情況下，我們完成了區域層次結構的構建，而在后一種情況下，我們為整個流圖再次構建出一個主體區域。

以下圖為例，圖(a)為控制流圖。此流程圖中有一個循環邊(B4->B2)。區域的層次結構如圖(b)所示，共有8個區域：

區域R1-R5分別代表塊B1-B5的葉區域。每個塊也是其區域中的出口塊。
區域R6表示流圖中唯一循環的主體；它包含區域R2、R3和R4以及三個區域間控制流邊R2->R3、R2->R4和R3->R4。它有R3和R4兩個出口塊，因為它們都有不包含在區域中的輸出邊。圖(c)顯示了R6簡化為單個節點的流程圖。請注意，邊R3->R5和R4->R5都被邊R6->R5取代。因為從R3和R4兩個區域的輸出都將到達到達R5的輸入，因此簡化后用一條邊代表之前兩條邊。
循環區域R7代表整個循環。它包括一個子區域R6和一個循環邊R4->R2。它還有兩個出口節點，也就是R3和R4。圖(d)顯示了整個循環簡化到R7后的流程圖。
最后，主體區域R8是頂部區域。它包括三個區域，R1、R7、R5和三個區域間控制流邊R1->R2、R3->R5和R4->R5。當我們將流程圖縮小到R8時，它將成為一個單一節點。由于其頭B1沒有循環邊，因此不需要將此主體區域減少為循環區域。

6、處理不可簡化流圖

對于不可簡化流圖，我們建議使用迭代數據流分析算法來進行數據流分析。但是如果只是偶爾處理不可簡化流圖的話，可以使用節點分裂方法進行分析。

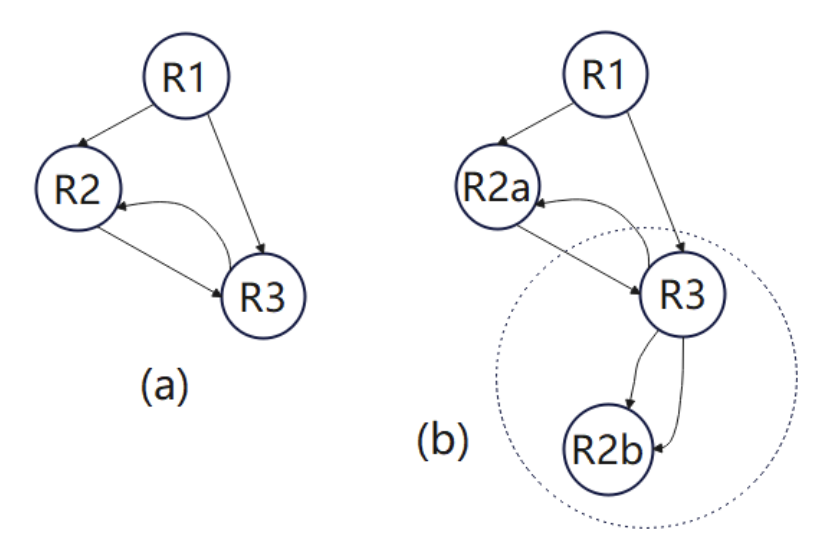
下面圖(a)就是一個典型的不可簡化流圖。R2和R3之間存在循環，但R2和R3又都不占支配地位，導致我們無法進一步解析該圖。我們選擇一些區域R（如R2），該區域R具有多個前置節點（R2的前置節點為R1和R3），并且不是整個流圖的頭。如果有k個前置節點，則制作流圖R的k個副本，并將每個前置節點連接到R的不同副本。這里需要注意，只有區域的頭才可能有該區域之外的前置節點。在識別新的循環邊并構建其區域后，這種節點分裂使得區域數量減少。由此產生的流圖可能仍然不可簡化，但通過分裂階與新的循環被識別并折疊到區域的階段交替使用，我們最終只剩下一個區域，即流圖已經被約化。

圖(b)中所示的分裂將邊R2b->R3變成了循環邊，此時R3支配R2b,這兩個區域可以合并為一個新區域。由此產生的三個區域（R1、R2a和新區域）形成一個非循環圖。此時，我們可以將整個流程圖簡化為單個區域。一般來說，可能需要額外的拆分，在最壞的情況下，基本塊的總數可能會成為原始流圖中塊數的指數。