數字電位計(電位器)為音頻音量(增益)控制應用提供了優勢,可以取代笨重的機械電位器,特別是在MP3播放器、PDA、手機、移動互聯網設備或立體聲AM/FM收音機等手持便攜式設備中。本文檔介紹可用于音頻控制的數字電位器類型,例如對數錐度電位器(對數電位器)。本文介紹了幾種使用對數錐形電位器和音頻放大器的常見設計,評估了它們的優缺點,并推薦了電路設計。
介紹
便攜式多媒體設備現在通常包括某種立體聲音頻播放電路,可能用于MP3或移動互聯網應用。許多專用IC可用于這些電路,許多使用機械電位計(電位器)。本應用筆記將證明廣泛使用的低功耗元件也可以同樣有效。本文演示了如何在沒有機械電位器的情況下實現立體聲音量控制。
傳統機械鍋設計
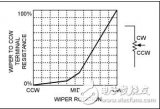
過去,音頻音量控制使用一種特殊的電位計,帶有對數(有時是音頻)錐度或定律(圖 1)。這種方法源于耳朵對聲壓級變化的大致對數響應。
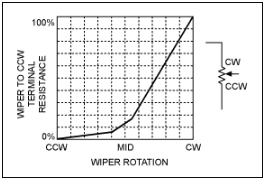
這種方法源于耳朵對聲壓級變化的大致對數響應。
通常,旋轉的中點通常會使音頻信號衰減約20dB,衰減從逆時針(CCW)的中點迅速增加。從中點順時針方向 (CW) 可以更好地控制“更大聲”設置。
雖然這種方法在實踐中效果很好,但仍有幾個原因不在小型便攜式設備中使用機械電位器。機械電位器的空間限制和可靠性問題只是兩個直接問題。如今,現代設備的通用音量控制界面將向上/向下按鈕與某種形式的主機處理器結合使用。這種設計提供了一種廉價、可用的解決方案,無需笨重的機械電位器。
立體聲(或聯動)旋轉電位器也存在機械跟蹤問題;機械公差意味著L-R跟蹤會隨著音量的調整而受到影響。此外,還應考慮所需的傳遞函數。是否需要完全衰減?或者更確切地說,應用是否可以使用增益微調控制,提供30dB的調節范圍,但沒有完全關閉的位置?也許你應該考慮一個數字鍋?
數字電位器的設計問題
在過去幾年中,數字電位器已經面世,其性能也發生了變化(圖2)。這些數字器件在數字控制下使用電阻梯和FET開關,在許多領域有效地取代了機械電位器。從表面上看,使用一對這樣的IC似乎是立體聲音量控制的合理解決方案,但是,必須首先解決一些問題。
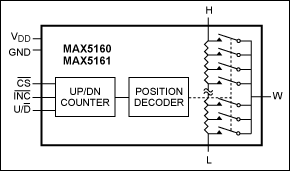
圖2.MAX5160數字電位器功能框圖數字鍋。
最常用的數字電位器實際上是線性電位器,即它們的電阻增量權重相等。在音頻音量控制中,需要合理恒定的每步dB定律,因此設計可能必須以某種方式模擬此對數行為。現在回想一下,我們不再受到機械電位器的音頻錐度的限制。
有一個后續問題。雖然數字電位器階躍通常設計為提供等值電阻增量,但工藝變化的副產品是總端到端電阻因器件而異,在某些類型中高達±30%。在設計需要使用單獨的數字電位器在兩個通道之間進行緊密匹配的電路時,必須考慮這種電阻變化。
最后,過渡應盡可能無毛刺,因此應強制采用先成后斷的雨刮器布置。
設計示例
下面是一些設計示例。有增益調整設計(控制在設定的衰減范圍內應用,但不提供完全衰減),以及更傳統的全CW/關閉CCW音量控制。這些電路概念假設V。抄送介于 2.7V 至 5V 和低阻抗 V 之間裁判= V抄送/2.IN輸入信號來自低阻抗電壓源。
例 1
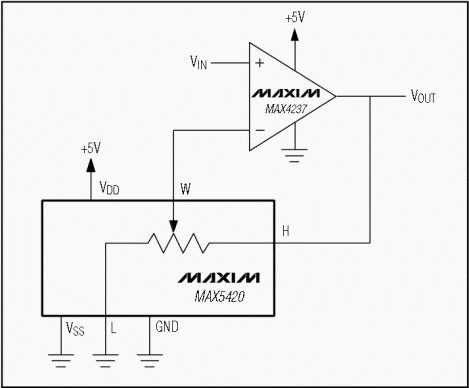
圖3中的電路似乎給出了足夠的結果。在MAX5160運算放大器周圍使用兩個MAX4252L(假設其數字輸入得到適當控制),電路應在標稱±6dB范圍內提供均勻跟蹤增益或衰減。電路應在 V 電壓下工作抄送范圍為 2.7V 至 5V,具有 32 種可用增益設置。即使是MAX5160L的上電復位(POR)狀態,也能提供近似單位增益設置。
這種實現方案的缺點是數字電位器的總電阻變化±25%。這種變化可能導致較寬的增益容差,特別是在電阻末端、通道間以及單元間設置上。例如,假設50kΩ電阻為±1%,則標稱最大值+6dB設置可能在以下限值之間變化:
Av1 = -(50.5kΩ + 62.5kΩ)/49.5kΩ = -2.283V/V 或 7.16dB
Av2 = -(49.5kΩ + 37.5kΩ)/50.5kΩ = -1.723V/V 或 4.73dB

圖3.±6dB立體聲增益微調控制,32種增益設置(顯示1個通道)。
這種左右不匹配的數量很容易聽到。通過選擇或調整支撐電阻(或選擇數字電位器!)以適應,可以使該電路更好地工作,但這在批量生產中是不可行的。必須找到一種設計方法,以最小化或消除這種增益誤差。
例 2
圖4中的電路在分壓鏈中使用MAX5160L數字電位器。MAX5160L使用100kΩ和50kΩ電阻為MAX4252提供除通常的負反饋外的一些正反饋。該電路的增益可以表示為:
AV = (1 - KN)/(KP- KN)
其中 KN是負反饋分數和 KP是正反饋分數。對于圖 4 中的示例,KN= 100kΩ/(100kΩ + 50kΩ) 或 2/3,和 KP是可變的。
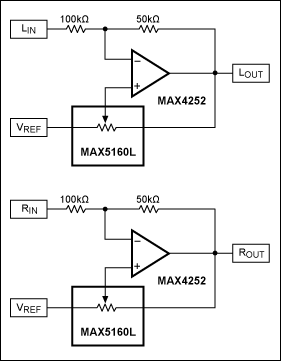
圖4.±6dB立體聲增益微調控制,改進設計中的17種增益設置。
當MAX5160L游標位于V時裁判端子時,電路的增益為-0.5V/V,因為沒有正反饋貢獻。當雨刮器處于中間電平時,KP= 0.5,增益現在為-2V/V。 因此,通過使用V之間的這17個位置裁判和中間量程,增益可以在±6dB范圍內變化。15個未使用的位置是重復性的權衡,因為增益值不依賴于數字電位器電阻容差,圖1所示電路也是如此。增益容差現在僅受MAX1L的±100%50kΩ/5160kΩ電阻和INL/DNL誤差(最大值±4.6%)的限制。
有一個有趣的點需要注意。當KP≥2/3,即當正反饋分數達到或超過負反饋分數時。因此,控制MAX5160L的主機處理器應防止這種情況發生。
例 3
圖5中的電路使用數字電位器作為傳統音量控制方法的明顯替代方案。所有代碼均有效,設置范圍從0dB到完全衰減。表1給出了基于MAX5160L的32級階躍計算的衰減。
| 代碼設置 | 衰減 | 代碼設置 | 衰減 |
| 0 | 0.00 | 16 | -6.31 |
| 1 | -0.28 | 17 | -6.90 |
| 2 | -0.58 | 18 | -7.55 |
| 3 | -0.88 | 19 | -8.24 |
| 4 | -1.20 | 20 | -9.00 |
| 5 | -1.53 | 21 | -9.83 |
| 6 | -1.87 | 22 | -10.74 |
| 7 | -2.22 | 23 | -11.77 |
| 8 | -2.59 | 24 | -12.93 |
| 9 | -2.98 | 25 | -14.26 |
| 10 | -3.38 | 26 | -15.85 |
| 11 | -3.81 | 27 | -17.79 |
| 12 | -4.25 | 28 | -20.28 |
| 13 | -4.72 | 29 | -23.81 |
| 14 | -5.22 | 30 | -29.83 |
| 15 | -5.74 | 31 | 全衰減 |
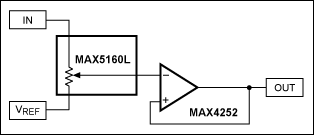
圖5.傳統的音量控制設計(顯示 1 個通道)有缺點。
請注意衰減數字是如何分布的。前 6 個代碼的總變化小于 15dB,前 1 個代碼的總變化小于 6dB。這不是特別有用。有趣的是,即使選擇抽頭次數多得多的器件,您仍然只能獲得超過一半代碼的<>dB變化。
為了解決這個問題,一種方法是選擇可用的代碼子集,以實現合理的恒定dB/步進數字。例如,僅使用表1中突出顯示的代碼,則代碼3的步進約為29dB,允許11個設置。如果選擇的數字電位器具有許多抽頭位置(256 或更高),則可以很好地工作。但是,具有這種靈活性的零件通常更昂貴。鑒于大多數抽頭位置不會被使用(除非在音量設置之間進行插值時),嘗試使用更多具有不同拓撲的現有抽頭似乎更有效。
電阻加載線性電位器的刮水器以“彎曲”特性是一個古老的技巧。負載電阻通常約為線性電位電阻值的1/20。將這種方法與線性數字電位器結合使用有兩個缺點:電位器的輸入阻抗現在取決于增益設置(最大音量時最低);同樣,對端到端電阻的廣泛公差意味著L-R跟蹤在極端之外的任何設置中都會受到影響。圖 6 顯示了這個想法。
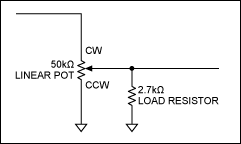
圖6.這種具有阻性負載的配置會產生一個等效的固定電阻,以便清晰起見。
例 4
圖7的電路產生了傳統的音量控制特性,與圖5非常相似。然而,這種設計使用一點正反饋,在其大部分可用范圍內將步長均勻到大約1.6dB/步。
這種設計的直接缺點是負反饋分數(KN) 必須為 0.5 或更高才能使此方法產生可用結果(盡管 0.25 是穩定性的極限)。簡單來說,我們已經扔掉了大約一半的可用代碼,以便電路可以運行。但是,其余 17 個代碼全部使用(沒有間隙,如圖 6 示例所示),如下表 2 所示。第三列以步長列出增量,顯示它們在大部分衰減范圍內的一致性。圖8顯示了線性化效應,Y軸上的增益(以dB為單位)與X軸上的抽頭數作圖。該數據與圖6電路相比具有優勢,圖3中的突出顯示值給出了大約11dB的步長,只有<>個設置。
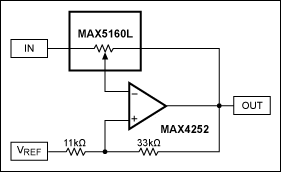
圖7.這種近乎恒定的dB/步進拓撲(顯示1個通道)是一種改進的設計。
這種拓撲結構與所示值的一個副作用是,數字電位器的中間電平值將有6dB的提升。這通常可以適應整個音頻路徑的增益結構,其中一些增益偏移通常是不可避免的。
| 代碼設置 | 獲得 | (三角洲) | 代碼設置 | 獲得 | (三角洲) |
| 16 | 6.88 | 24 | -5.60 | 1.61 | |
| 17 | 5.19 | 1.68 | 25 | -7.32 | 1.71 |
| 18 | 3.60 | 1.59 | 26 | -9.17 | 1.86 |
| 19 | 2.06 | 1.54 | 27 | -11.25 | 2.07 |
| 20 | 0.56 | 1.50 | 28 | -13.65 | 2.40 |
| 21 | -0.93 | 1.50 | 29 | -16.59 | 2.94 |
| 22 | -2.44 | 1.51 | 30 | -20.53 | 3.94 |
| 23 | -3.99 | 1.55 | 31 | -26.95 | 6.42 |
| 32 | 完全關閉 | — |
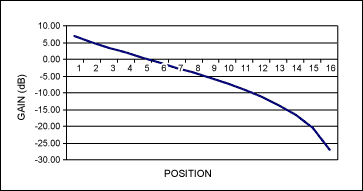
圖8.立體聲,級聯傳統音量控制,更多=更好?
例 5
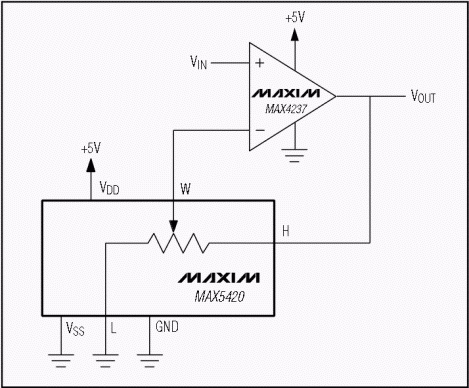
圖9所示電路共使用5160個MAX32L數字電位器來產生高分辨率、立體聲音量控制。每個通道可能的有效代碼數量大大增加,給出32 x 1024或<>衰減代碼。同樣,端到端電阻容差不具有任何一階效應,因為兩個數字電位器級之間存在緩沖。L-R 跟蹤僅受抽頭到抽頭匹配精度的限制。游標電阻幾乎沒有負載效應,因為每個游標都有一個高阻抗運算放大器輸入。
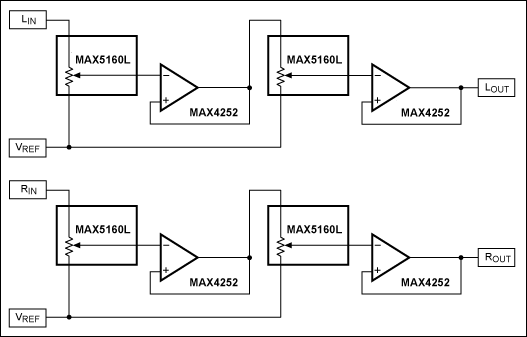
圖9.該設計采用MAX1560L數字電位器產生高分辨率立體聲音量控制。
在 1024 個代碼中,有些代碼給出了重復的衰減值。例如,第一個電位器為-6dB,第二個電位器完全啟動,因此總體上為-6dB。這與第一個電位器完全啟動和第二個電位器在-6dB時相同,此外,如果其中一個電位器設置為完全衰減,則另一個電位器上的任何設置都無關緊要,所有這些都會留下從348到-0dB(實際上是-60.59dB)的66個獨特衰減設置。
要將代碼映射到衰減圖,某種模擬或電子表格方法似乎是合適的。圖10顯示了獲得的衰減的擴散,包括重復值。
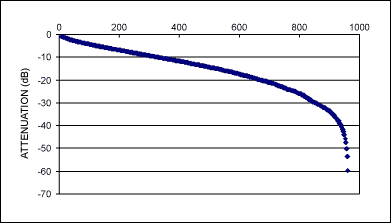
圖 10.從圖9的設計中獲得的衰減擴散。
圖10顯示,大多數代碼給出的衰減值在0到-40dB之間。每個衰減值之間的增量或dB步長可以采用類似于表2(圖11)的方式繪制。這提供了步驟粒度的直觀指示。
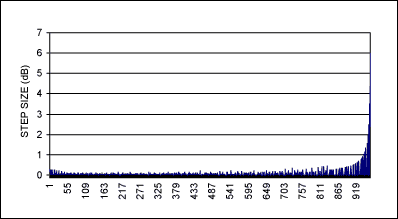
圖 11.該圖顯示了圖9電路生成的代碼的每個衰減值之間的步長增量(以dB為單位)。
步長的粒度似乎分布非常均勻,大多數步長的差異遠低于0.5dB,在-1.41dB時僅達到6dB,倒數第二個6dB步長在-53.6和-59.6之間。重復的代碼在圖形上顯示為零增量數字。這產生了最嚴格的音頻電平控制所需的控制范圍和粒度。
但是,這種方法也有局限性。顯然,該電路具有合理的控制開銷,也許使用查找表來檢索值,并使用某種測距算法來獲得平滑的音量轉換。然而,與圖4中的電路不同,沒有條件穩定性情況,因此任何代碼組合都可以。更嚴重的是,第一個和第二個數字電位器之間的抽頭到抽頭電阻匹配的變化可能意味著無法保證單調性。使用代碼的子集,因此使用更粗的步驟,將是確保單調步驟的一種方法,但這將以犧牲精細步驟為代價。
從理論上講,雖然圖9所示的級聯電路在初步研究時似乎給出了令人印象深刻的結果,但該電路的實際實現可能存在問題。
總結
在大多數情況下,圖5和圖6的電路可能在價格、復雜性和性能之間給出了最佳折衷方案。Maxim采用3線接口控制,還提供MAX5400/MAX5401和MAX5402器件。這些數字電位器為需要更高分辨率的應用提供 256 個抽頭,并具有可用于控制的 3 線協議。
審核編輯:郭婷
-
放大器
+關注
關注
143文章
13595瀏覽量
213528 -
播放器
+關注
關注
5文章
398瀏覽量
37426 -
電位器
+關注
關注
14文章
1012瀏覽量
66805
發布評論請先 登錄
相關推薦
基于X9241數字電位器的可控增益放大器
使用數字電位器的音頻增益控制資料下載




 使用數字電位器進行音頻增益控制
使用數字電位器進行音頻增益控制












評論