這篇綜合文章涵蓋了模擬濾波器的所有方面。它首先介紹基本類型：一階和二階濾波器、高通和低通濾波器、陷波和全通濾波器以及高階濾波器。然后，本教程介紹了不同實現的特性，例如巴特沃茲濾波器、切比切夫濾波器、貝塞爾濾波器、橢圓濾波器、狀態變量濾波器和開關電容濾波器。

介紹

易于使用，集成式開關電容濾波器對許多應用具有吸引力。本文通過描述濾波器產品并解釋控制其操作的概念來幫助您為此類設計做好準備。

從一個簡單的積分器開始，我們首先開發一種直觀的有源濾波器方法。然后，我們介紹了狀態變量濾波器及其開關電容形式的實現等實際實現。本文介紹的具體集成濾波器包括Maxim的MAX7400系列高階開關電容濾波器。

一階濾波器

積分器過濾器

積分器（圖1a）是數學上最簡單的濾波器，它構成了大多數現代集成濾波器的構建模塊。考慮一下我們對集成商的直觀了解。如果在輸入端施加直流信號（即零頻率），輸出將描述一個線性斜坡，該斜坡的幅度不斷增長，直到受到電源的限制。忽略該限制，積分器在零頻率下的響應是無限的，這意味著它在零頻率下有一個極點。（極點存在于傳遞函數的值變為無窮大的任何頻率下。

我們還知道，積分器的增益隨著頻率的增加而減小，并且在高頻下，輸出電壓幾乎變為零。增益與頻率成反比，因此在對數/對數坐標上繪制時，其斜率為-1（即，波特圖上的-20dB/十倍頻程，圖1b）。

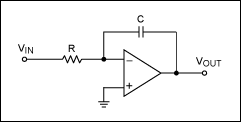
圖 1a.一個簡單的RC積分器。

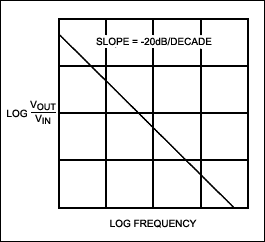
圖 1b.簡單積分器的波特圖。

您可以輕松地將傳遞函數導出為：

VOUT/VIN = XC/R = (1/sC)/R = -1/(sCR) = -ω0/s

其中 s 是復頻變量 σ + jω 和 ω0為 1/RC。如果我們將s視為頻率，則此公式證實了增益與頻率成反比的直觀感覺。稍后，在討論實際過濾器的實現時，我們將回到集成商。

簡單的RC低通濾波器

稍微復雜的濾波器是簡單的低通RC型（圖2a）。其特性（傳遞函數）為：

VOUT/VIN = (1/sC)/(R + 1/sC) = 1/(1 + sCR) = ω0/(s + ω0)

當 s = 0 時，函數減少到 ω0/哦0，即團結。當 s 增加到無窮大時，函數接近零，因此這是一個低通濾波器。當 s = -ω 時0，分母為零，函數的值為無窮大，表示復頻率平面中的極點。在圖2b中，傳遞函數的大小與s繪制，其中s的實分量σ朝向我們，正虛部jω朝右。-ω 處的極點0是顯而易見的。振幅以對數方式顯示，以強調函數的形式。對于積分器和RC低通濾波器，頻率響應在無限頻率下趨于零。簡單地說，在s = ∞處有一個零。這個零圍繞復平面。

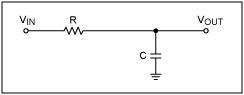
圖 2a.一個簡單的RC低通濾波器。

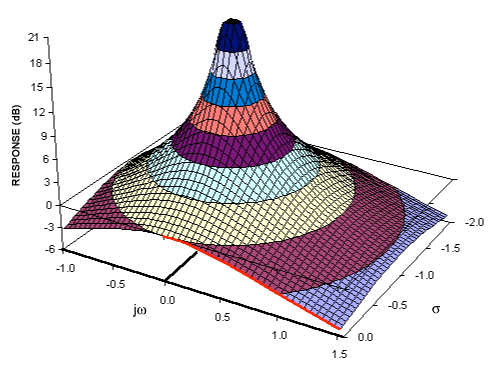
圖 2b.RC低通濾波器的復雜功能。

但是，s中的復數函數與電路對實際頻率的響應有何關系呢？在分析電路對交流信號的響應時，我們使用表達式jωL表示電感的阻抗，使用1/jωC表示電容器的阻抗。當使用拉普拉斯變換分析瞬態響應時，我們使用sL和1 / sC作為這些元件的阻抗。相似之處立即顯現出來。交流分析中的jω實際上是s的虛部，如前所述，它由實部s和虛部jω組成。

如果我們在上述任何方程中用jω代替s，我們就會得到電路對角頻率ω的響應。在圖 2b 的復圖中，沿正 jω 軸的 σ = 0，因此 s = jω。因此，該函數沿該軸的值是濾波器的頻率響應。我們沿jω軸對函數進行了切片，并通過沿正jω軸為函數值添加一條粗線來強調RC低通濾波器的頻率-響應曲線。更熟悉的波特圖（圖2c）在形式上看起來不同，只是因為頻率是對數表示的。

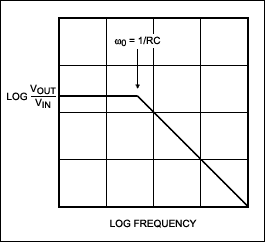
圖 2c.低通濾波器的波特圖。

雖然復數頻率的虛部jω有助于描述對交流信號的響應，但實部σ有助于描述電路的瞬態響應。因此，從圖2b可以看出RC低通濾波器的響應與積分器的響應相比。低通濾波器的瞬態響應更穩定，因為它的極點位于復平面的負實半部分。重述，低通濾波器對階躍函數輸入做出衰減指數響應;積分器做出無限響應。對于低通濾波器，-σ軸下方的極點位置意味著ω0，時間常數更短，因此瞬態響應更快。相反，靠近jω軸的極點會導致更長的瞬態響應。

到目前為止，我們已經將一些簡單電路的數學傳遞函數與它們在復頻平面中的相關極點和零點相關聯。從這些函數中，我們推導出了電路的頻率響應（以及波特圖）及其瞬態響應。由于積分器和RC濾波器在其傳遞函數的分母中只有一個s，因此它們各只有一個極點。也就是說，它們是一階濾波器。

但是，從圖1b可以看出，一階濾波器不能提供非常選擇性的頻率響應。為了更貼近應用需求定制過濾器，我們必須轉向更高的階數。從現在開始，我們將使用 f（s） 而不是繁瑣的 V 來描述傳遞函數外/在在.

二階低通濾波器

二階濾波器具有2在分母和復平面中的兩個極點。通過在無源電路中使用電感和電容，或者創建由電阻器、電容器和放大器組成的有源電路，可以獲得這種響應。例如，考慮圖3a中的無源LC濾波器。我們可以證明它的傳遞函數具有以下形式：

?（s） = XC/（R + XL+ XC） = （1/sC）/[R + sL + （1/sC）] = 1/（LCS2+ 遙控S+ 1)

如果我們定義：

ω02 = 1/LC and Q = ω0L/R = 1/(RCω0)

然后：

?（s） = 1/[（s/ω0)2+ s/（ω0Q） + 1] = ω02/[s2+ s（ω0/Q） + ω02]

哪里哦0是濾波器的特征頻率，Q是品質因數（R越低意味著Q越高）。

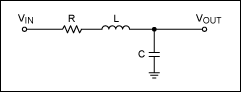
圖 3a.RLC低通濾波器。

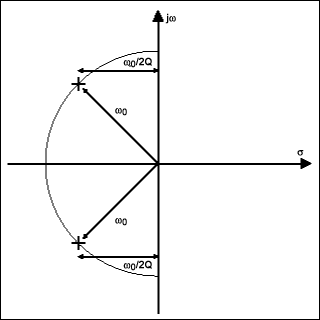
圖 3b.RLC低通濾波器的極點零點圖。

極點出現在分母變為零的 s 值處;也就是說，當2+ 不銹鋼0/Q+z02= 0。我們可以通過記住 ax 的根來解決這個方程2+ bx + c = 0 由下式給出：

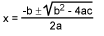
在這種情況下，a = 1， b = ω0/Q， 和 c = ω02.術語（b2- 4ac） 等于 ω02（1/Q2- 4).因此，如果 Q 小于 0.5，則兩個根都是實數，并且位于負實軸上。該電路的行為非常類似于級聯中的兩個一階RC濾波器。這種情況不是很有趣，所以我們只考慮 Q > 0.5 的情況，這意味著 （b2- 4ac）為負數，根很復雜。

因此，實部是 -b/2a，即 -ω0/2Q，并且兩個根共有。根的虛部在符號上是相等和相反的。計算根在復平面中的位置，我們發現它們位于 ω 的距離處0（相關的數學，簡單但乏味，將留給更受虐狂的讀者練習。

變化哦0更改極點與原點的距離。減小 Q 會使兩極彼此靠近;增加 Q 會使半圓中的極點彼此遠離并朝向 jω 軸。當 Q = 0.5 時，兩極在 -ω 處相遇0在負實軸上。在這種情況下，相應的電路相當于兩個級聯的一階濾波器，如前所述。

現在我們應該檢查二階函數的頻率響應，看看它如何隨 Q 變化。和以前一樣，圖4a將函數顯示為曲面，在由復平面和垂直幅度矢量形成的三維空間中表示。此外，Q = 0.707，您可以立即看到響應是低通濾波器。

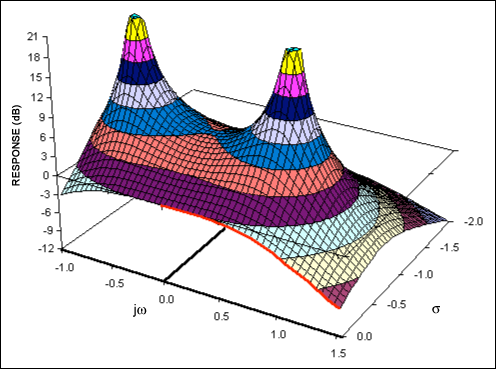
圖 4a.二階低通濾波器的復函數（Q = 0.707）。

增加 Q 值會使圓形路徑中的極點向 jω 軸移動。圖 4b 顯示了 Q = 2 的情況。由于極點離jω軸更近，因此它們對頻率響應的影響更大，從而在通帶的高端產生峰值。

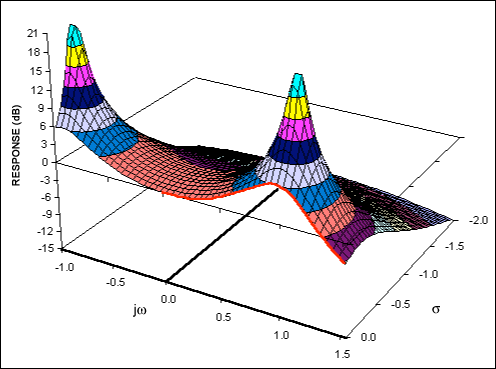
圖 4b.二階低通濾波器的復函數（Q = 2）。

對濾波器的瞬態響應也有影響。由于極點的負實部較小，輸入階躍函數將導致濾波器輸出端出現振鈴。Q值越低，振鈴越小，因為阻尼越大。如果Q變為無窮大，則極點到達jω軸，在s = ω處引起無限頻率響應（不穩定和連續振蕩）0.在圖3a的LCR電路中，除非R = 0，否則這種情況是不可能的。然而，對于包含放大器的濾波器，這種情況確實是可能的，必須在設計過程中加以考慮。

二階濾波器提供變量 ω0和 Q，它允許我們將極點放置在復平面中我們想要的任何位置。盡管如此，這些極點必須以復共軛對的形式出現，其中實部相等，虛部具有相反的符號。這種極點放置的靈活性是一個強大的工具，使二階級成為許多開關電容濾波器的有用元件。與一階情況一樣，二階低通傳遞函數隨著頻率增加到無窮大而接近零。然而，二階函數的下降速度是其兩倍，因為2分母的因素。結果是無窮遠處的雙零。

在討論了一階和二階低通濾波器之后，我們現在需要在兩個方向上擴展我們的概念：我們將討論其他濾波器配置，例如高通和帶通部分，然后我們將討論高階濾波器。

高通和帶通濾波器

為了將低通濾波器變為高通濾波器，我們將s平面從內向外轉動，使低頻高，高頻低。無限頻率的雙零變為零頻率;零頻率下的有限響應變為無限。為了完成這種轉換，我們使s = ω02/s，因此當ω02/s 0時s∞，反之亦然。在 ω0 處，s 的舊值和新值相同。s = 1 處的雙零變為零;我們在 S = 0 時的有限響應移動到無窮大，產生一個高通濾波器：

?(s) = ω02/[(ω04/s2) + (ω03/Qs) + ω02]

如果我們將分子和分母乘以s2/ω02,

?（s） = s2/[s2+ （sω0/Q） + ω02]

此形式與以前相同，只是分子是 s2而不是 ω02. 換句話說，我們可以通過改變分子并保留分母來將低通函數轉換為高通函數。

波特圖為低通到高通變換提供了另一種視角。圖5a顯示了二階低通函數的波特圖：平坦到截止頻率，然后以-40dB/十倍頻程下降。乘以 s2為此功能增加+40dB/十倍頻程斜率。額外的斜率提供低于截止頻率的低頻滾降;高于截止值時，它通過消除原始的-5dB/十倍頻程斜率來提供平坦的響應（圖40b）。

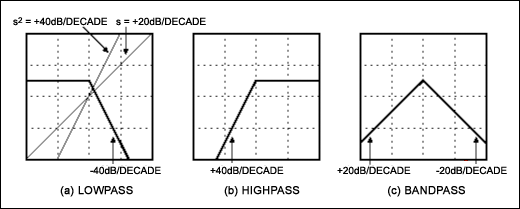
圖5.二階濾波器的波特圖。

我們可以使用相同的想法來生成帶通濾波器。將低通響應乘以s，即可獲得+20dB/十倍頻程斜率。然后，凈響應比截止值低+20dB/十倍頻程，高于截止值-20dB/十倍頻程。這會產生圖5c中的帶通響應：

?（s） = ω0s/[s2+ （sω0）/Q） + z02]

請注意，二階帶通濾波器的截止速率是其他類型的一半。這是因為可用的40dB/十倍頻程斜率必須在濾波器的兩個裙邊之間共享。

總之，歸一化形式的二階低通、帶通和高通函數具有相同的面額，但它們的分子為 ω02哦0s 和 s2分別。

陷波和全通濾波器

陷波或帶阻濾波器抑制特定頻段內的頻率，同時通過所有其他頻段。同樣，您可以通過更改標準二階特征的分子來導出此濾波器的傳遞函數：

?(s) = (s2 + ωZ2)/s2 + (sω0/Q) + ω02

考慮極限情況。當 s = 0 時，f（s） 減小到 ω跟2/哦02，這是有限的。當 s 為∞時，方程減少到 1。在 s = jω 時跟，分子變為零，f（s） 變為零（雙零，實際上是因為2在分子中），并且我們具有陷波濾波器的特征。在陷波頻率高于和低于陷波時，增益將有所不同，除非ω跟= 哦0.陷波濾波器方程也可以表示為：

?(s) = s2 + (ωZ2)/s2 + (sω0/Q) + ω02 =
[s2/s2 + (sω0/Q) + ω02] + [ωZ2/s2 + (sω0/Q) + ω02]

這可以簡單地說明。陷波濾波器基于低通和高通特性的總和。我們在實際濾波器實現中利用這一事實，從現有的高通和低通響應生成陷波響應。我們通過添加兩個響應來創建零似乎很奇怪，但它們的相位關系使之成為可能。

最后，還有全通濾波器，其形式為：

?（s） = [s2- （sω0/Q） + ω02]/[s2+ （sω0/Q） + ω02]

該響應的極點和零點對稱地放置在jω軸的兩側，如圖6所示。這些極點和零點的影響精確抵消，以提供電平和均勻的頻率響應。似乎一根電線可以更便宜地提供這種效果。然而，與導線不同，全通濾波器提供了相位響應隨頻率的有用變化。

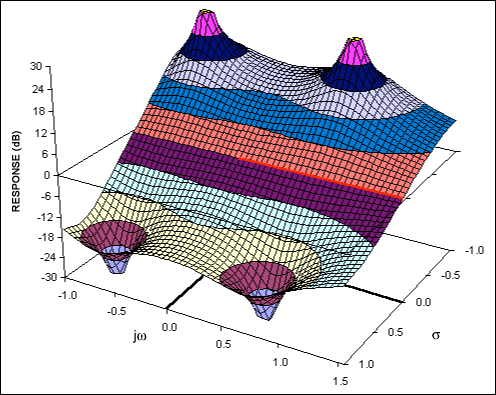
圖6.二階全通濾波器的復雜函數。

高階濾波器

我們很幸運不必單獨處理高階濾波器，因為任何長度的 s 中的多項式都可以分解為一系列二次項（如果多項式是奇數，則加上單個一階項）。例如，五階低通濾波器可能具有傳遞函數：

?（s） = 1/[s5 + a4s4 + a3s3 + a2s2 + a1s + a0]

其中所有 a0 都是常量。我們可以將分母分解為：

?（s） = 1/[（s2 + sω1/Q1 + ω12）（s2 + sω2/Q2 + ω22）（s + ω3）]

這與：

?（s） = [1/（s2 + sω1/Q1 + ω12）] × [1/（s2 + sω2/Q2 + ω22）] × [1/（s + ω3）]

最后一個方程表示一個濾波器，我們可以在物理上實現為兩個二階部分和一個一階部分，全部級聯。

這種配置簡化了設計，使復頻平面中的極點和零點響應可視化變得更加容易。我們知道，每個二階項貢獻一個復共軛極對，一階項在負實軸上貢獻一個極點。如果傳遞函數在分子中具有高階多項式，則該多項式也可以分解，這意味著二階部分將是低通部分以外的其他內容。

使用上述合成原理，我們可以簡單地通過將極點和零點放置在復頻平面的不同位置來構建各種各樣的濾波器。然而，大多數應用只需要有限數量的可能性。對他們來說，許多早期的實驗者，如巴特沃斯和切比切夫，已經制定了細節。

巴特沃斯過濾器

許多應用中常見的一種濾波器要求在通帶內保持平坦的響應，但之后盡可能急劇地切斷。您可以通過在半圓形軌跡周圍排列間距相等的低通濾波器的極點來獲得該響應。結果將是巴特沃茲濾波器。例如，圖7a的零極圖表示巴特沃茲濾波器的四階類型。

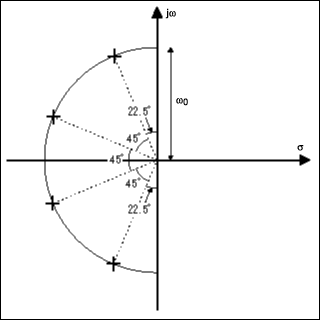
圖 7a.四階巴特沃茲低通濾波器的極點零圖。

圖7a中的極點具有不同的Q值，但它們都具有相同的ω0因為它們與原點的距離相同。對應于該濾波器的三維表面（圖7b）說明了當最低Q極點的影響開始消失時，下一個極點接管，直到極點用完并且響應以-80dB/十倍頻程下降。

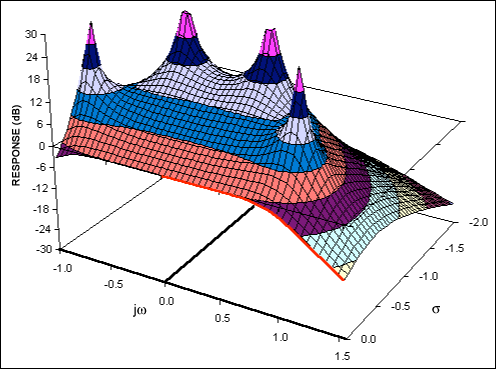
圖 7b.四階巴特沃茲低通濾波器的復雜函數。

您可以構建高通、帶通和其他濾波器類型的巴特沃茲版本，但這些濾波器的極點不會排列在一個簡單的半圓中。在大多數情況下，您首先設計一個低通濾波器，然后應用轉換來生成其他類型的濾波器。

切比切夫過濾器

通過將極點靠近jω軸（增加它們的Qs），我們可以制造出頻率截止比巴特沃茲更陡峭的濾波器。這種安排有一個缺點：每個極點的影響將在濾波器響應中可見，從而產生幅度變化，稱為通帶中的紋波。然而，通過適當的極點排列，變化可以相等，這導致了切比切夫濾波器。

通過將每個極點以相同的比例靠近 jω 軸，使極點位于橢圓上，您可以從巴特沃斯推導出切比切夫濾波器（圖 8a）。圖8b顯示了每個極點如何為通帶紋波貢獻一個峰值。將極點移近jω軸會增加通帶紋波，但在阻帶中提供更突然的截止。因此，切比切夫濾波器在紋波和截止之間提供了權衡。在這方面，巴特沃茲濾波器，其中通帶紋波設置為零是切比切夫的一個特例。

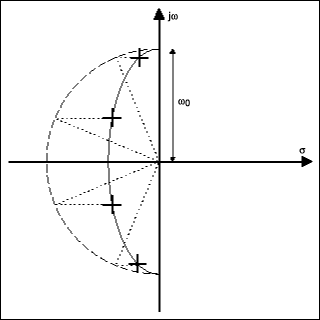
圖 8a.四階切比切夫低通濾波器的極點零圖。

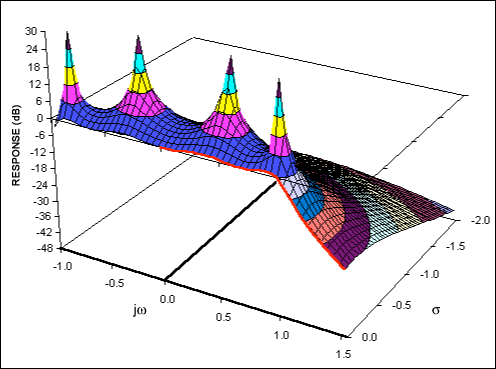
圖 8b.四階切比切夫低通濾波器的復雜函數。

貝塞爾濾波器

具有尖銳截止的巴特沃斯和切比切夫濾波器帶有從其極點在 s 平面中的位置可以明顯看出的懲罰。使極點靠近jω軸會增加它們的Q值，從而降低濾波器的瞬態響應。可能會導致響應邊沿出現過沖甚至振鈴。

貝塞爾濾波器代表了與北海相反方向的權衡。貝塞爾極點位于離jω軸更遠的軌跡上（圖9）。瞬態響應得到改善，但代價是阻帶的截止值不那么陡峭。

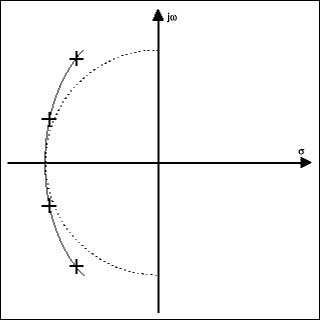
圖9.四階貝塞爾低通濾波器的極點零點圖。

橢圓濾波器

通過增加最接近通帶邊緣的極點的Q，可以獲得比切比切切夫更清晰的阻帶截止的濾波器，而不會產生更多的通帶紋波。單獨這樣做會產生增益峰值，但您可以通過在阻帶底部提供一個零來補償峰值。必須沿阻帶間隔額外的零點，以確保濾波器響應保持在所需的阻帶衰減水平以下。圖10a顯示了這種類型的零極圖：橢圓濾波器。圖10b顯示了相應的傳遞函數表面。正如您可能想象的那樣，橢圓濾波器的高Q極點產生的瞬態響應甚至比切比切夫還要差。

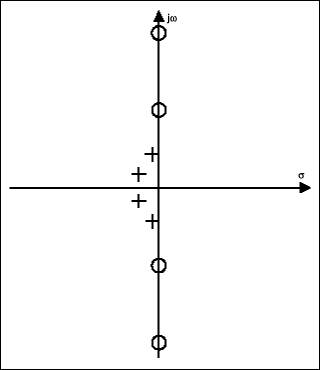
圖 10a.四階橢圓低通濾波器的極點零點圖。

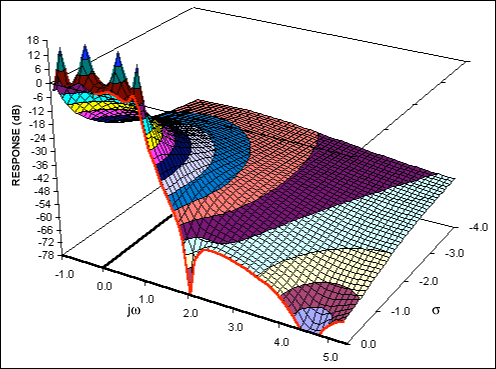
圖 10b.四階橢圓低通濾波器的復雜函數。

請注意，所描述的所有濾波器都具有與極點相同的零數。（必須如此，否則傳遞函數將不是無量綱表達式。例如，橢圓濾波器在阻帶中沿jω軸將其零點間隔開。在貝塞爾、巴特沃斯和切比切夫的情況下，所有的零都在無窮大處彼此重疊。由于分子中沒有顯式零，因此這些濾波器類型有時稱為全極點濾波器。

現在，我們已經擴展了我們的概念，不僅涵蓋了一階和二階濾波器，還涵蓋了高階濾波器，包括一些特別有用的情況。現在是時候從抽象理論轉向討論實際電路了。

狀態變量篩選器

如前所述，我們可以從一階和二階構建塊構造任何濾波器。您可以將一階濾波器視為二階濾波器的特例。因此，我們的基本構建塊應該是二階部分，從中我們可以導出低通、高通、帶通、陷波或全通特性。

狀態變量濾波器是二階部分的便捷實現。它使用兩個級聯積分器和一個求和結，如圖11所示。

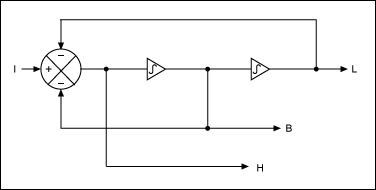
圖 11.二階狀態變量篩選器。

我們知道積分器的特性只是ω0/s.但是為了在簡化數學的同時演示原理，我們可以假設兩個積分器都有ω0= 1，并且它們的特性只是 1/s。然后，我們可以為圖 11 中的每個積分器編寫方程：

L = B/s 或 B = sL

B = H/s 或 H = sB = s2L

圖11中求和結的公式很簡單：

H = I - B - L

如果我們使用積分器方程代入 H 和 B，我們得到：

s2L = I - sL - L

Or

s2L + sL + L = I

在這種情況下：

L（s2 + s + 1） = I

Or

L/I = 1/（s2 + s + 1）

公式22是經典的歸一化低通響應。因為 B = sL 和 H = s2L，所以：

B/I = s/（s2 + s + 1） 和 H/I = s2/（s2 + s + 1）

公式23分別顯示了經典帶通和高通響應。

因此，一個濾波器同時提供低通、帶通和高通輸出。我們可以創建實際值為 ω 的實際濾波器0和 Q 通過構建具有 ω 的積分器從這些方程中得出0≠ 1 并將因子反饋到值為 ≠1 的求和交匯點。

理論上，您可以通過級聯兩個以上的積分器來創建高階濾波器。一些集成電路濾波器使用這種方法，但它有缺點。若要對這些篩選器進行編程，必須計算高階多項式的系數值。此外，一長串集成器引入了穩定性問題。通過將自己限制在二階部分，我們的優勢是可以直接使用 ω0以及與每個極點關聯的 Q 變量。

開關電容濾波器

無論架構如何，所有有源濾波器的特性都取決于其RC時間常數的精度。由于集成電阻和電容的典型精度約為±30%，因此設計人員在嘗試對集成濾波電路中的元件使用絕對值時會受到阻礙。然而，芯片上的電容器值之比可以精確控制在2000年的<>部分左右。開關電容濾波器使用這些電容比來實現精度，而無需精密的外部元件。

在圖12所示的開關電容積分器中，組合C.1開關模擬電阻。

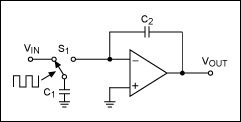
圖 12.開關電容積分器。

開關 S1 以時鐘頻率 fCLK 連續切換。當S1位于左側時，電容C1向VIN充電。當它向右切換時，C1將電荷轉儲到積分器的求和節點中，并從該節點流入電容器C2。每個時鐘周期內C1上的電荷為：

Q = C1VIN

因此，傳輸到求和結的平均電流為：

I = QfC = C1VIN × fCLK

請注意，電流與 V 成正比在，所以我們具有與值電阻相同的效果：

R = VIN/I = 1/(C1fCLK)

積分器的 ω0因此：

ω0 = 1/RC2 = C1fCLK/C2

因為哦0與兩個電容器的比率成正比，其值可以非常精確地控制。此外，該值與時鐘頻率成正比，因此您可以通過更改f來改變濾波器特性時鐘，如果需要。但開關電容是一個采樣數據系統，因此不完全等同于時間連續RC積分器。事實上，這些差異給設計師帶來了三個問題。

首先，通過開關電容器的信號由時鐘頻率調制。如果輸入信號包含接近時鐘頻率的頻率，則它們可能會相互調制，并在系統帶寬內產生雜散輸出頻率。對于許多應用來說，這不是問題，因為輸入帶寬已經限制在時鐘頻率的一半以下。否則，開關電容濾波器之前必須有一個抗混疊濾波器，該濾波器可去除輸入頻率高于時鐘頻率一半的任何分量。

其次，積分器輸出（圖12）不是線性斜坡，而是時鐘頻率下的一系列步進。在由開關注入的電荷引起的階躍轉換處可能存在小尖峰。如果濾波器之后的系統帶寬遠低于時鐘頻率，則這些像差可能不是問題。否則，必須在開關電容濾波器的輸出端再次添加另一個濾波器，以消除時鐘紋波。

第三，開關電容濾波器的行為與理想的時間連續模型不同，因為輸入信號每個時鐘周期僅采樣一次。當濾波器的極點頻率接近時鐘頻率時，濾波器輸出會偏離理想值，特別是對于低Q值時。但是，您可以計算這些效應，并在設計過程中允許它們。

考慮到上述情況，最好保持時鐘與中心頻率的比值盡可能大。開關電容濾波器的典型比率范圍約為28：1至200：1。例如，MAX262允許的最大時鐘頻率為4MHz，因此使用28：1的最小比率可獲得140kHz的最大中心頻率。在低端，開關電容濾波器的優點是可以處理低頻，而無需使用令人不安的大R和C值。您只需降低時鐘頻率即可。

結論

本文介紹了與開關電容有源濾波器相關的概念和術語。如果您已經掌握了此處介紹的材料，您應該能夠理解大多數濾波器數據手冊。

審核編輯：郭婷