光波在介質(zhì)中的傳播可由介質(zhì)中的麥克斯韋方程組精確描述。物質(zhì)方程描述了感應電磁場（D、B）與電磁場（E、H）、極化場（P、M）之間的關系。不考慮非線性效應，而僅在線性光學的情形下討論，那么極化場與電磁場之間呈線性關系。利用上述這些方程可以推導出在各向同性、均勻、無磁性、無自由電荷及電流的介質(zhì)中的波動方程。電場與磁場之間存在固定的關系，所以只需要考慮電場即可，磁場可以由電場得到。

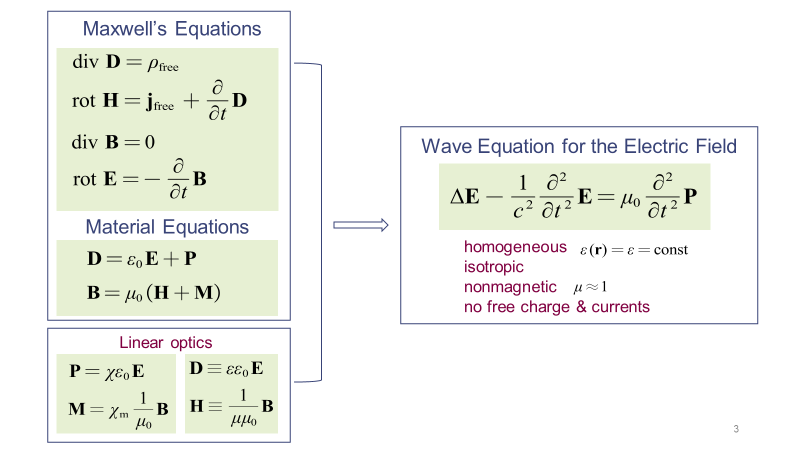
在求解波動方程時，如果不考慮介質(zhì)的色散，而且假定電磁波沿z軸方向傳播，那么波動方程可以進行簡化。簡化后的波動方程有一個最基本的特解——平面波解，而其他任何復雜的波都可以展開成平面波解的線性疊加。因此，暫時只需要討論平面波解。平面波是一種橫向電磁波，其電場、磁場的方向，以及波傳播的方向三者兩兩垂直。當平面波從光疏介質(zhì)傳輸?shù)焦饷芙橘|(zhì)中時，其頻率ν不發(fā)生變化，但是波數(shù)k、波速vp和波長λ均會發(fā)生改變。

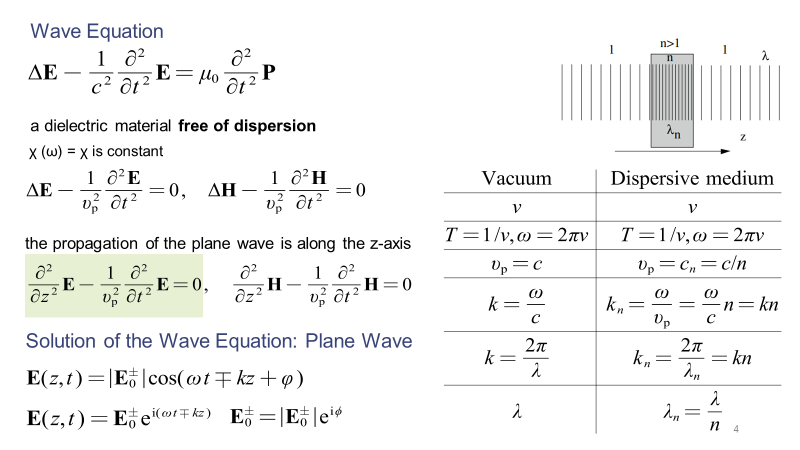
平面波的常見偏振狀態(tài)可分為線偏振、圓偏振和橢圓偏振三種。最一般的情況就是橢圓偏振，這種偏振狀態(tài)的電場由沿x軸和y軸兩個方向、具有一定相位差且振幅任意的振動矢量疊加得到。逆著波傳播的方向觀察，橢圓偏振狀態(tài)總的電場振動向量的軌跡是一個橢圓。當沿x軸和y軸的振動相位差為0時，總的電場振動向量的軌跡是一條線段，此時的平面波處于線偏振狀態(tài)；當沿x軸和y軸的振動相位差為±π/2，且振幅相等時，總的電場振動向量的軌跡是一個圓，這樣的平面波處于圓偏振狀態(tài)。

電場和磁場之間的叉乘用來定義Poynting矢量，也即能流密度。對于平面波來說，能流密度矢量與傳播時的等相位面垂直，即沿著波數(shù)k的方向。在計算能流密度與能量密度的瞬時值時需要注意利用的是平面波電場和磁場的實數(shù)部分；而計算能流密度與能量密度的時間平均值時，需要對代入復數(shù)電磁場后的最終結(jié)果取實部，并乘以1/2。

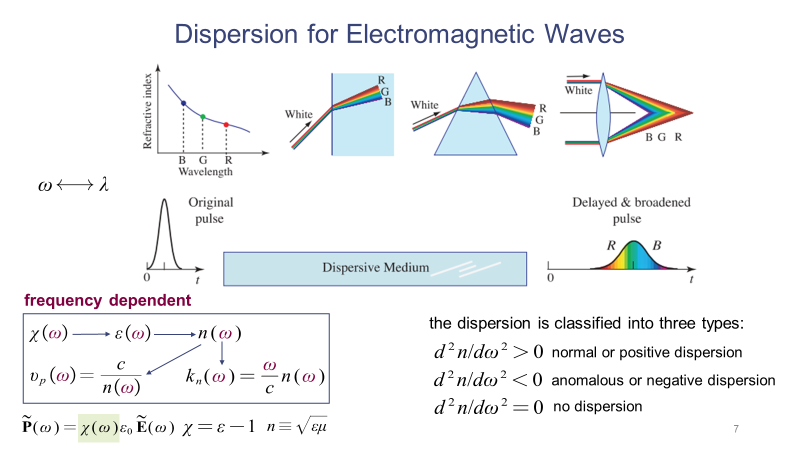
下面介紹平面波在色散介質(zhì)中的傳播。我們可以用兩個例子來理解色散。第一個是白光光束經(jīng)過介質(zhì)折射后的“擴束”現(xiàn)象；第二個是光脈沖經(jīng)過介質(zhì)傳播后的脈沖寬度展寬現(xiàn)象。這些現(xiàn)象源于不同頻率的光在介質(zhì)中傳播時具有不同的折射率，使得光的偏折角度和傳播速度會彼此不同。這種折射率對光頻率（或波長）的依賴就導致了各種色散現(xiàn)象，色散現(xiàn)象分為三種：正常色散、反常色散和無色散。在介質(zhì)正常色散的區(qū)間內(nèi)，長波長的光波傳播速度要比短波長的光波快，反常色散則剛好相反。

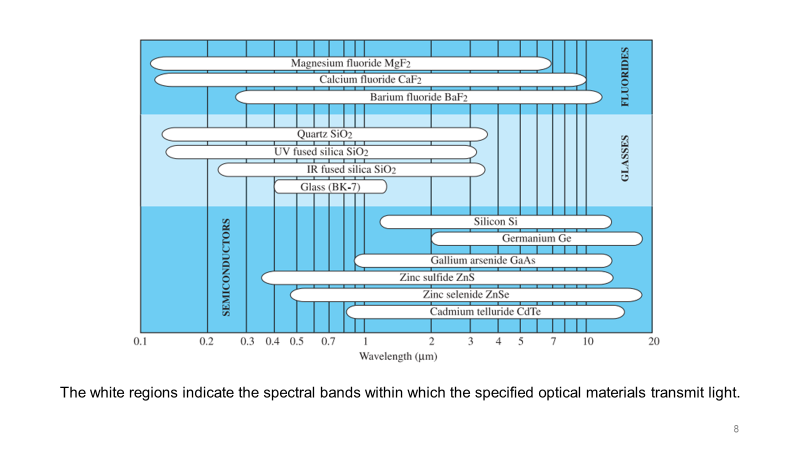
除了色散，不同光學材料擁有不同的可透光波長范圍，由光學材料的吸收特性所決定。

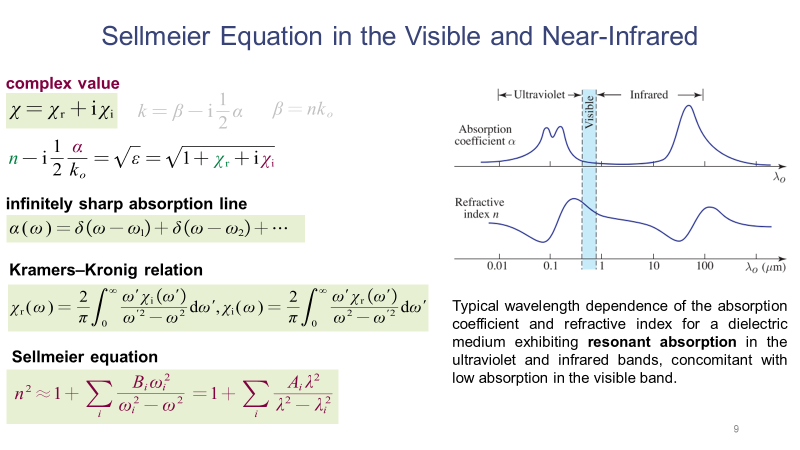
介質(zhì)的色散（折射率的頻率依賴性）和吸收與極化率密切相關。極化率通常為復數(shù)，其實部與折射率n相關，虛部與吸收系數(shù)α相關，并且極化率的實部和虛部滿足Kramers-Kronig關系，根據(jù)這一關系，知道實部和虛部中的一個就可以得到另一個。如果所關注的波長范圍遠離介質(zhì)的共振吸收頻率，那么可以將介質(zhì)的共振吸收峰近似為無限銳吸收線，也即可以用δ函數(shù)近似表示吸收系數(shù)，進而根據(jù)吸收系數(shù)α再求得折射率n的表達式，也即Sellmeier公式。

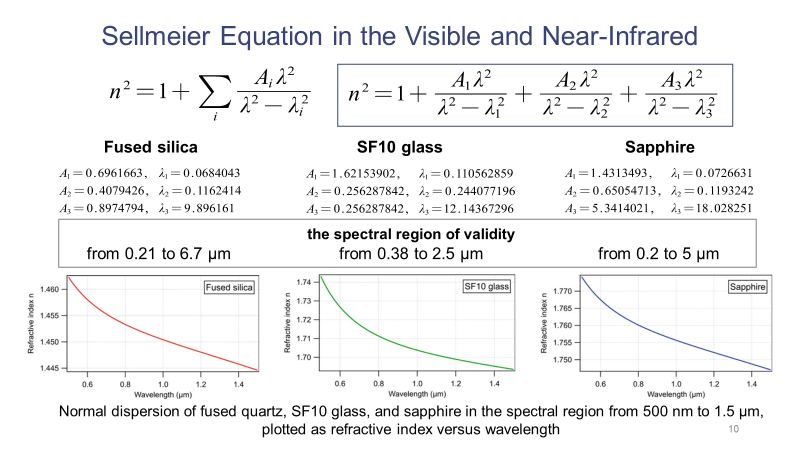
根據(jù)Sellmeier公式，對于特定的介質(zhì)，當知道該式中的各個參數(shù)的值，就可以得到折射率隨波長的變化關系。下面的幻燈片列舉了熔融二氧化硅、SF10玻璃和藍寶石這三種介質(zhì)利用Sellmeier公式得到折射率與波長的關系曲線。

當我們關注的波長小于200nm，到達真空紫外、極紫外甚至是X射線的區(qū)域時，由于介質(zhì)強烈的吸收，Sellmeier公式不再適用，這時需要利用新的計算公式來得到介質(zhì)的折射率。

在計算中需要用到的各種參數(shù)也可以通過查閱工具書得到，下面的幻燈片展示了碳（C）和鋁（Al）的計算結(jié)果。

以上從麥克斯韋方程組和物質(zhì)方程出發(fā)，推導得到波動方程，隨后討論平面波解的特性，最后介紹平面波在色散介質(zhì)中傳播時的色散現(xiàn)象，以及在不同波長范圍內(nèi)如何計算介質(zhì)的折射率。

審核編輯：劉清