狀態(tài)機(jī)模式是一種行為模式,通過(guò)多態(tài)實(shí)現(xiàn)不同狀態(tài)的調(diào)轉(zhuǎn)行為的確是一種很好的方法,只可惜在嵌入式環(huán)境下,有時(shí)只能寫(xiě)純C代碼,并且還需要考慮代碼的重入和多任務(wù)請(qǐng)求跳轉(zhuǎn)等情形,因此實(shí)現(xiàn)起來(lái)著實(shí)需要一番考慮。
近日在看到了一個(gè)狀態(tài)機(jī)的實(shí)現(xiàn),也學(xué)著寫(xiě)了一個(gè),與大家分享。
首先,分析一下一個(gè)普通的狀態(tài)機(jī)究竟要實(shí)現(xiàn)哪些內(nèi)容。
狀態(tài)機(jī)存儲(chǔ)從開(kāi)始時(shí)刻到現(xiàn)在的變化,并根據(jù)當(dāng)前輸入,決定下一個(gè)狀態(tài)。這意味著,狀態(tài)機(jī)要存儲(chǔ)狀態(tài)、獲得輸入(我們把它叫做跳轉(zhuǎn)條件)、做出響應(yīng)。
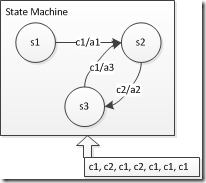
如上圖所示,{s1, s2, s3}均為狀態(tài),箭頭c1/a1表示在s1狀態(tài)、輸入為c1時(shí),跳轉(zhuǎn)到s2,并進(jìn)行a1操作。
最下方為一組輸入,狀態(tài)機(jī)應(yīng)做出如下反應(yīng):

當(dāng)某個(gè)狀態(tài)遇到不能識(shí)別的輸入時(shí),就默認(rèn)進(jìn)入陷阱狀態(tài),在陷阱狀態(tài)中,不論遇到怎樣的輸入都不能跳出。
為了表達(dá)上面這個(gè)自動(dòng)機(jī),我們定義它們的狀態(tài)和輸入類(lèi)型:
typedef int State;
typedef int Condition;
#define STATES 3 + 1
#define STATE_1 0
#define STATE_2 1
#define STATE_3 2
#define STATE_TRAP 3
#define CONDITIONS 2
#define CONDITION_1 0
#define CONDITION_2 1
在嵌入式環(huán)境中,由于存儲(chǔ)空間比較小,因此把它們?nèi)慷x成宏。此外,為了降低執(zhí)行時(shí)間的不確定性,我們使用O(1)的跳轉(zhuǎn)表來(lái)模擬狀態(tài)的跳轉(zhuǎn)。
首先定義跳轉(zhuǎn)類(lèi)型:
typedef void (*ActionType)(State state, Condition condition);
typedef struct
{
State next;
ActionType action;
} Trasition, * pTrasition;
然后按照上圖中的跳轉(zhuǎn)關(guān)系,把三個(gè)跳轉(zhuǎn)加一個(gè)陷阱跳轉(zhuǎn)先定義出來(lái):
// (s1, c1, s2, a1)
Trasition t1 = {
STATE_2,
action_1
};
// (s2, c2, s3, a2)
Trasition t2 = {
STATE_3,
action_2
};
// (s3, c1, s2, a3)
Trasition t3 = {
STATE_2,
action_3
};
// (s, c, trap, a1)
Trasition tt = {
STATE_TRAP,
action_trap
};
其中的動(dòng)作,由用戶(hù)自己完成,在這里僅定義一條輸出語(yǔ)句。
void action_1(State state, Condition condition)
{
printf("Action 1 triggered.\\n");
}
最后定義跳轉(zhuǎn)表:
pTrasition transition_table[STATES][CONDITIONS] = {
/* c1, c2*/
/* s1 */&t1, &tt,
/* s2 */&tt, &t2,
/* s3 */&t3, &tt,
/* st */&tt, &tt,
};
即可表達(dá)上文中的跳轉(zhuǎn)關(guān)系。
最后定義狀態(tài)機(jī),如果不考慮多任務(wù)請(qǐng)求,那么狀態(tài)機(jī)僅需要存儲(chǔ)當(dāng)前狀態(tài)便行了。例如:
typedef struct
{
State current;
} StateMachine, * pStateMachine;
State step(pStateMachine machine, Condition condition)
{
pTrasition t = transition_table[machine- >current][condition];
(*(t- >action))(machine- >current, condition);
machine- >current = t- >next;
return machine- >current;
}
但是考慮到當(dāng)一個(gè)跳轉(zhuǎn)正在進(jìn)行的時(shí)候,同時(shí)又有其他任務(wù)請(qǐng)求跳轉(zhuǎn),則會(huì)出現(xiàn)數(shù)據(jù)不一致的問(wèn)題。
舉個(gè)例子:task1(s1, c1/a1 –> s2)和task2(s2, c2/a2 –> s3)先后執(zhí)行,是可以順利到達(dá)s3狀態(tài)的,但若操作a1運(yùn)行的時(shí)候,執(zhí)行權(quán)限被task2搶占,則task2此時(shí)看到的當(dāng)前狀態(tài)還是s1,s1遇到c2就進(jìn)入陷阱狀態(tài),而不會(huì)到達(dá)s3了,也就是說(shuō),狀態(tài)的跳轉(zhuǎn)發(fā)生了不確定,這是不能容忍的。
因此要重新設(shè)計(jì)狀態(tài)機(jī),增加一個(gè)“事務(wù)中”條件和一個(gè)用于存儲(chǔ)輸入的條件隊(duì)列。修改后的代碼如下:
#define E_OK 0
#define E_NO_DATA 1
#define E_OVERFLOW 2
typedef struct
{
Condition queue[QMAX];
int head;
int tail;
bool overflow;
} ConditionQueue, * pConditionQueue;
int push(ConditionQueue * queue, Condition c)
{
unsigned int flags;
Irq_Save(flags);
if ((queue- >head == queue- >tail + 1) || ((queue- >head == 0) && (queue- >tail == 0)))
{
queue- >overflow = true;
Irq_Restore(flags);
return E_OVERFLOW;
}
else
{
queue- >queue[queue- >tail] = c;
queue- >tail = (queue- >tail + 1) % QMAX;
Irq_Restore(flags);
}
return E_OK;
}
int poll(ConditionQueue * queue, Condition * c)
{
unsigned int flags;
Irq_Save(flags);
if (queue- >head == queue- >tail)
{
Irq_Restore(flags);
return E_NO_DATA;
}
else
{
*c = queue- >queue[queue- >head];
queue- >overflow = false;
queue- >head = (queue- >head + 1) % QMAX;
Irq_Restore(flags);
}
return E_OK;
}
typedef struct
{
State current;
bool inTransaction;
ConditionQueue queue;
} StateMachine, * pStateMachine;
static State __step(pStateMachine machine, Condition condition)
{
State current = machine - > current;
pTrasition t = transition_table[current][condition];
(*(t- >action))(current, condition);
current = t- >next;
machine- >current = current;
return current;
}
State step(pStateMachine machine, Condition condition)
{
Condition next_condition;
int status;
State current;
if (machine- >inTransaction)
{
push(&(machine- >queue), condition);
return STATE_INTRANSACTION;
}
else
{
machine- >inTransaction = true;
current = __step(machine, condition);
status = poll(&(machine- >queue), &next_condition);
while(status == E_OK)
{
__step(machine, next_condition);
status = poll(&(machine- >queue), &next_condition);
}
machine- >inTransaction = false;
return current;
}
}
void initialize(pStateMachine machine, State s)
{
machine- >current = s;
machine- >inTransaction = false;
machine- >queue.head = 0;
machine- >queue.tail = 0;
machine- >queue.overflow = false;
}




 狀態(tài)機(jī)要實(shí)現(xiàn)哪些內(nèi)容
狀態(tài)機(jī)要實(shí)現(xiàn)哪些內(nèi)容