接下來的Matlab數(shù)值計算,將以電池建模的foster型等效電路為基礎(chǔ),在連續(xù)時間內(nèi)對電池進(jìn)行系統(tǒng)同定。
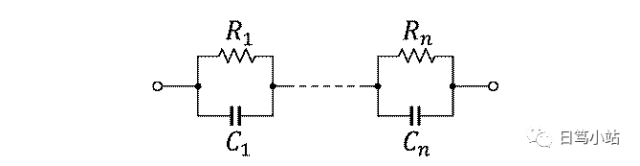
foster等效電路
首先,我們利用輸入輸出的數(shù)據(jù)來推測電池模型的參數(shù)。推測的參數(shù)為:
θ = [ R0 Rd Cd FCC SOC0 ] T

輸入輸出數(shù)據(jù)與SOC
電池的建模(Matlab)
數(shù)值實(shí)驗(yàn)用輸入出數(shù)據(jù)的生成:
[ex_batt.m]1
%%假想實(shí)驗(yàn)數(shù)據(jù)的作成
Te = 2*3600; %實(shí)驗(yàn)結(jié)束時刻[sec]
Ts = 1; %采樣周期[sec]
t = ( 0: Ts: Te );
N = length(t);
%輸入(電流)的設(shè)定
u = 40sawtooth( tsqrt(2)) + 10*sin(t) - 18;
%輸出(電壓)的生成
SOC0 = 95; %初期SOC[%]
FCC = 40*3600; %滿充電容量[C]
R0 = 0.450e-3; %電池內(nèi)阻[ohm]
Rd = 0.500e-3; %擴(kuò)散電阻[ohm]
Cd = 82000; %擴(kuò)散電容[F]
th0 = [ R0, Rd, Cd, FCC ];
Nd = 3; %foster等效電路的近似級數(shù)
[ f, h, A, C, ymodel ] = batterymodel_foster(Nd);
%Simulation
[ y0, x ] = ymodel( u, t, th0, [SOC0; zeros(Nd, 1)] );
SOC = x(1, :);
%含有誤差的采樣值的模擬
um = u + randn(1, N) * 0.1; %電流傳感器的誤差
ym = y0 + randn(1, N) * 0.01; %電壓傳感器的誤差
%波形
figure(3), hold on
subplot(3,1,1); plot(t/60, u)
ylabel('Current [A]'), xlim([0 Te/60]), ylim([-100 50)]
subplot(3,1,2); plot(t/60, y0)
ylabel('Voltage [V]'), xlim([0 Te/60]), ylim([3.2 4.2)]
subplot(3,1,3); plot(t/60, SOC)
ylabel('SOC [%]'), xlim([0 Te/60]), ylim([0 100)]
xlabel('Time [min]),
上述 “m file” 里面使用的函數(shù) “batterymodel_foster" , 用以下方式記述。
[batterymodel_foster.m]
function [ f, h, A, C, ymodel ] = batterymodel_foster(Nd)
n = 1:Nd;
%參數(shù)矢量與物理常數(shù)的關(guān)系定義
R0 = @(th) th(1);
Rd = @(th) th(2);
Cd = @(th) th(3);
FCC = @(th) th(4);
A = @th blkdiag(0, -pi^2/4 * diag((2*n-1).^2)/Rd(th)/Cd(th();
B = @th [100/FCC(th); 2*ones(Nd,1)/Cd(th)];
f = @(x, u, th) A(th)*x + B(th)*u;
h = @(x, u, th) SOC2OCV(x(1,:)) + [0, ones(1, Nd)]*x+R0(th)*u;
%利用數(shù)值微分來計算SOC的雅可比數(shù)列
C = @(x) [numdiff(@SOC2OCV, x(1)), ones(1, Nd)];
%yhat:預(yù)測輸出的函數(shù)
function [y, x] = proto_ymode(u, t, th, x0)
x = lsim(ss(A(th), B(th), eye(Nd+1), 0), u, t, x0, 'zoh')';
y = h(x, u, th);
end
ymodel = @proto_ymodel;
end
上述的雅可比數(shù)列A,C為狀態(tài)推算時使用。
我們再來看看偏微分的數(shù)值計算。
[numdif.m]
function [dfdx] = numdiff(f, x)
n = length(x);
h = eye(n)*1e-5;
dfdx = arrayfun(@(k) (f(x+h(:, k)) - f(x-h(:,k)))/(2*h(k, k)), 1:n);
end
另外,SOC-OCV特性的簡易模型我們可以用以下m file來記述。
[SOC2OCV.m]
function ocv=SOC2OCV(SOC)
%系數(shù)設(shè)定
E0 = 4.14;
K1 = 0.237;
K2 = -0.0516;
K3 = 1.05e-3;
K4 = 0.183;
mode = @(soc) E0 + K1.*log(soc/100) + K2.*log(1-soc/100) - K3./soc*100 - K4.*soc/100;
ocv = model(SOC);
ocv(SOC >98) = numdiff(model, 98)*(SOC(SOC >98)-98) + model(98);
ocv(SOC 2) = numdiff(model, 2)*(SOC(SOC< 2)-2) + model(2);
end
下面繼續(xù)[ex_batt.m]來進(jìn)行連續(xù)時間里的電池系統(tǒng)同定,轉(zhuǎn)而來推算模型的參數(shù)。
[ex_batt.m]2
%%連續(xù)時間系統(tǒng)同定
yhat = @(th) ymodel(um, t, th(1:4), [th(5); zeros(Nd, 1)]);
%初期推算值
thhat0 = [1e-3, 1e-3, 1e5, 30*3600, 80];
%輸出誤差最小化的參數(shù)推算
thhat = Isqnonlin(...
@(th) ym-yhat(th.*thhat0), thhat0./thhat0, [ ], [ ],...
optimoptions(@Isqnonlin, 'Display', 'iter',...
'Algorithm', 'levenberg-marquardt')) .*thhat0
綜如上述所訴,在連續(xù)時間內(nèi)利用系統(tǒng)同定的方法,從實(shí)驗(yàn)得到的輸入輸出數(shù)據(jù),可以定義內(nèi)含物理現(xiàn)象的電池模型的參數(shù)。
電池狀態(tài)的推定
眾所周知,電池的狀態(tài)主要包括SOC(剩余電量)和SOH(剩余壽命)。
SOC的推定方法可以總結(jié)為:
- 依據(jù)放電試驗(yàn)的SOC測定
- 基于電池端子電壓的SOC推定
- 基于OCV測試的SOC推定
- 依據(jù)安時積分法的SOC推定
- 基于模型的SOC推定

SOH的推定方法可以總結(jié)為:
- 利用完全充放電測試容量的SOH推定
- 依據(jù)內(nèi)部電阻查表的SOH推定
- Bookkeeping的SOH推定
- 基于模型的SOH推定
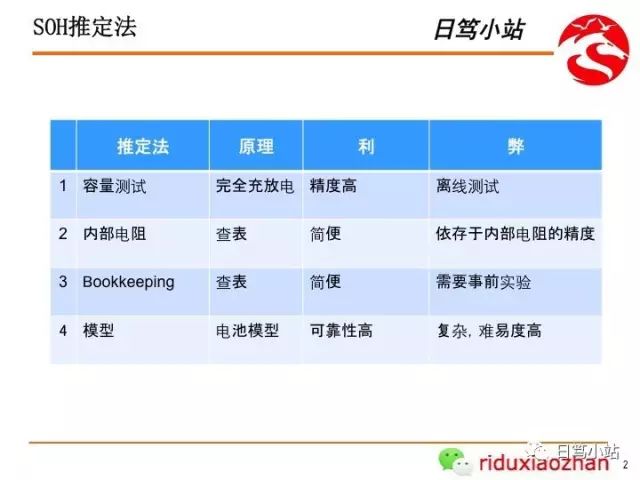
內(nèi)部電阻的推定方法可以總結(jié)為:
- 依據(jù)I-V特性(電流電壓特性)的線性回歸的內(nèi)部電阻推定
- 從step跳躍應(yīng)答的內(nèi)部電阻推定
- 依據(jù)電阻測試的內(nèi)部電阻推定
- 基于模型的內(nèi)部電阻推定

雖然有各種推算方法,但是我們需要根據(jù):要求精度,使用環(huán)境,硬件條件,在線連續(xù)推定的必要性等等來具體判斷用什么方法。
下面我們就給出比較復(fù)雜的利用卡爾曼濾波以及安時積分推算SOC的Matlab建模方法。
[ex_batt.m]3
%%利用EKF的狀態(tài)推定
%離散時間的狀態(tài)空間建模
f_ct = @(x, u) f(x, u, th0); %模型參數(shù)的固定
f_dt = c2d_euler(f_ct, Ts); %euler法的離散化
%fd的雅可比數(shù)列
Ad = expm(A(th0)*Ts); %f的雅可比解析計算
Q = diag([0.1Ts)^2, 1e-6ones(1, Nd)]); %系統(tǒng)外亂
R = 0.01^2; %觀測外亂
xhat = zeros(Nd+1, N); %狀態(tài)推算值
P = zeros(Nd+1, Nd+1, N); %推定分散
%初期推算值
SOChat0 = OCV2SOC(ym(1));
xhat(:,1) = [SOChat0; zeros(Nd,1)];
P(:,:,1) = diag([1e2, 1e-4*ones(1, Nd)]);
%更新時間
for k=2:N
[xhat(:,k),P(:,:,k)] =...
ekf(@(x) f_dt(x, um(k-1)), @x h(x, um(k), th0),...
@(x) Ad, C, Q, R, ym(k), xhat(:,k-1), P(:,:,k-1));
end
%表示結(jié)果
figure, plot_SOC(t, xhat(1,:), squeeze(P(1,1,:))',SOC);
EKF_RMSE = sqrt(mean((xhat(1,:) - SOC).^2,2));
%%安時積分法
SOC_cc = zeros(1, N);
SOC_cc(1) =SOChat(0);
for k=1:N-1
SOC_cc(k+1) = SOC_cc(k) + um(k)*Ts/FCC*100;
end
%表示結(jié)果
figure, plot_SOC(t, SOC_cc, [ ], SOC);
CC_RMSE = sqrt(mean((SOC_cc - SOC).^2,2));
上述euler的離散時間的狀態(tài)方程式變化方法為:
[c2d_euler.m]
function fd = c2d_euler(fc, h)
fuction x_new = fproto(x, u)
x_new = x + h*fc(x, u);
end
fd = @fproto;
end
SOC推算結(jié)果的表示
[plot_SOC.m]
function [ ] = plot_SOC(t, SOChat, P, SOC)
subplot(2,1,1), hold on
plot(t/60, SOC, 'r', 'LineWidth', 2)
plot(t/60, SOChat, 'b', 'LineWidth', 0.5)
xlim([0 t(end)/60]), ylim([0 100]);
xlabel('Time [min]'), ylabel('SOC [%]')
legend('True', 'Estimated', 'Location', 'Best')
box on
subplot(2,1,2), hold on
if ~isempty(P)
hold on
patch([t, fliplr(t)]/60,...
[(SOChat-SOC-2*sqrt(P)), fliplr(SOChat-SOC+2*sqrt(P))],...
' ','FaceColor', [0.5, 0.5, 1], 'FaceAlpha', 0.5,...
'EdgeAlpha', 0)
end
plot(t/60, SOChat-SOC, 'b')
plot([0 t(end)/60], [0 0], 'r', 'LineWidth', 2)
xlabel('Time [min]'), ylabel('Error [SOC%]')
xlim([0 t(end)/60]), ylim([-5 3]);
box on
end
上述為線性卡爾曼濾波的推算方法,非線性卡爾曼濾波的matlab建模方式基本相同,這里就不做介紹了。另外,本文是以EV為對象所建模,以HEV為對象時,由于電流波形的差異,推定的結(jié)果會有變故。HEV的剎車回生充電,內(nèi)燃機(jī)回生充電,SOC都是在50%附近控制,所以對于輸入的電流波形,不會有低頻率的成分。
對于實(shí)際使用電池的系統(tǒng)來說,有著電池組內(nèi)的誤差,生產(chǎn)誤差,環(huán)境溫度誤差等各項影響因素,所以未來我們使用模型推算電池狀態(tài)時,不僅要考慮到這些誤差因素的影響,更要考慮到鋰電池材料進(jìn)化的影響。未必復(fù)雜的算法適用于每個產(chǎn)品,我們需要根據(jù)實(shí)際的條件以及性價比等各種綜合因素來挑選推算的方法,希望讀者朋友們互相切磋,共同進(jìn)步。
-
SoC芯片
+關(guān)注
關(guān)注
1文章
615瀏覽量
34955 -
MATLAB仿真
+關(guān)注
關(guān)注
4文章
176瀏覽量
19945 -
卡爾曼濾波
+關(guān)注
關(guān)注
3文章
166瀏覽量
24661 -
電池系統(tǒng)
+關(guān)注
關(guān)注
9文章
390瀏覽量
29950
發(fā)布評論請先 登錄
相關(guān)推薦
卡爾曼濾波的原理說明
如何在單片機(jī)上實(shí)現(xiàn)卡爾曼濾波詳細(xì)計算方法和程序概述
基于擴(kuò)展卡爾曼濾波的SOC估算仿真
卡爾曼濾波的數(shù)學(xué)基礎(chǔ)
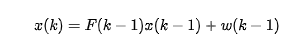




 電池SOC估算中的安時積分與卡爾曼濾波的數(shù)值計算方法
電池SOC估算中的安時積分與卡爾曼濾波的數(shù)值計算方法











評論