1.概述
橢球擬合是一種用于校準加速度計傳感器的方法。該方法假設各軸之間相互直,加速度傳感器在靜止狀態(只受重力的情況下),在三維空間中,各個姿態的x,y,z軸的重力點都在一個球面上。然而,由于各軸之間都會有偏差,所以各姿態重力點都落在一個橢球面上。橢球的中心即為加速度的偏移量,也就是校準值。 橢球擬合的核心方法是最小二乘法。 最小二乘法,也稱為最小平方法,用于通過最小化殘差的平方和來找到一條最佳擬合直線或曲線,從而找到自變量和因變量之間的關系。目的是:用于找到一組參數,使得模型的預測值與觀測值之間的平方誤差最小化。換句話說,它找到了最能代表變量之間關系的直線或曲線。它可以應用于線性回歸、多項式回歸和其他類型的回歸分析。 而線性回歸是一種基于最小二乘法的統計方法,用于建立自變量和因變量之間的線性關系模型。
2.加速度計的工作原理[1]
在這里再簡單的單獨介紹一下加速度的工作原理,前面也寫過一篇《MEMS 慣性傳感器 01-加速度計&陀螺儀工作原理》的博文詳細介紹了加速度計和陀螺儀的工作原理。 我們依據姿態傳感器的各軸的方向來想象有這樣一個立方體的盒子,盒子里裝有一個球。 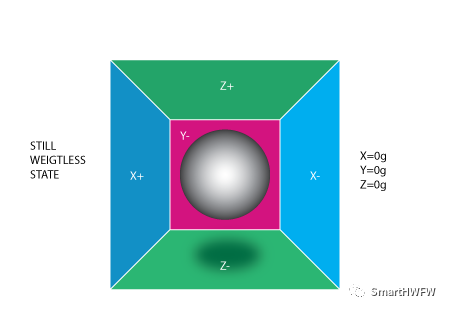
01
假設我們把這個盒子放進太空(沒有重力場),此時處于靜止狀態,三個軸的加速值都為[0, 0, 0]g。 如果我們突然將盒子向左移動(以加速度 1g = 9.8m/s^2 加速它),球將撞到 X-。然后,我們測量球施加到 X- 的壓力,并在X軸上輸出[-1, 0, 0]g 的值。 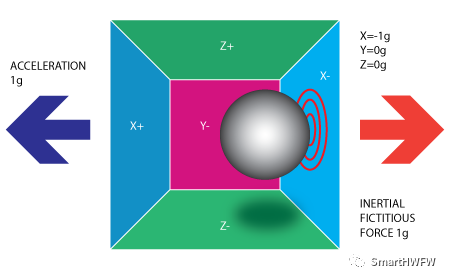 note:加速度計實際上將檢測到與加速度矢量方向相反的力。
note:加速度計實際上將檢測到與加速度矢量方向相反的力。
02
現在我們把立方體的盒子放在存在重力的地球上,Z 軸向上放在地球上,盒體內的球受到地球重力的影響會落在 Z- 內壁上,并在內壁上施加 [0, 0, -1]g 的值。在這種情況下,盒子沒有移動,但我們仍然在 Z 軸上得到 -1g 的讀數。球施加在內壁上壓力是由重力引起的。 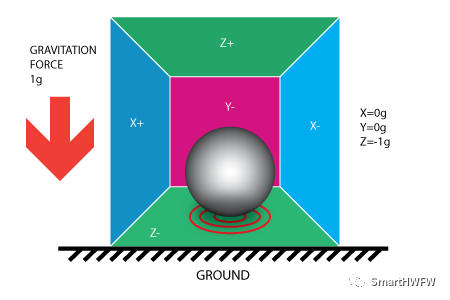
04
我們將盒子傾斜 45° 時,球將接觸 Z 和 X- 兩個面墻,將重力加速度正交分解,測得的X、Z軸的值為都為 [-g/√2, 0, -g/√2] 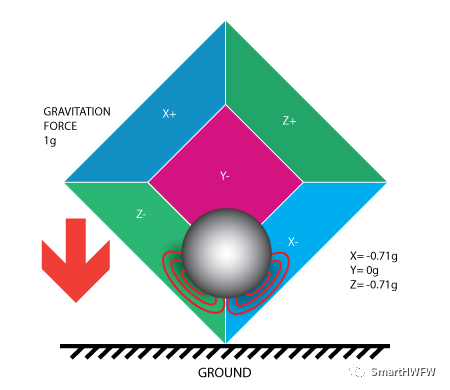
3.橢球擬合方法
01
橢球擬合算法描述 橢球擬合,可對多個位置(N)進行測量,并可進行組合以找到未知數(偏移、增益和交叉軸增益)。 和正六面體校準相比,正立面體需要準確的翻轉傳感器設備6次。 但是,對于橢球擬合,不需要知道傳感器的真實參考源,因為唯一的要求是真實參考源的模數是常數(X、Y 和 Z 的平方和的平方根)。 對于加速度計的情況:要僅測量重力,傳感器不得有任何其他加速度;那么真實參考源的模數就是重力的模數 橢球擬合算法數學理論可以在網上找很多,我參考閱讀的是:橢圓/球擬合法推導(快速入門)這篇[2] https://blog.csdn.net/qq_39667840/article/details/106607279
02
橢球擬合流程 1)橢球面的標準方程為: 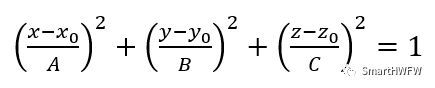 ?需要擬合的參數有六個,他們分別是橢球的中心和半軸長 ? ?2)將標準方程寫成一般形式為:
?需要擬合的參數有六個,他們分別是橢球的中心和半軸長 ? ?2)將標準方程寫成一般形式為: 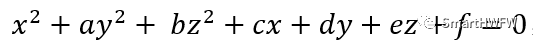 通過對參數a、b、c、d、e、f的求解間接求出參數 x0 、y0 、z0 、A、B、C ? ?3)建立誤差方程
通過對參數a、b、c、d、e、f的求解間接求出參數 x0 、y0 、z0 、A、B、C ? ?3)建立誤差方程 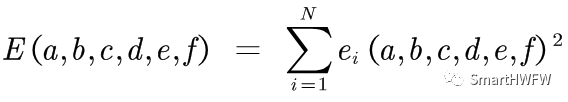 ? ?4)改寫成目標函數
? ?4)改寫成目標函數 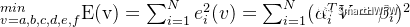 ? 5)根據線性最小二乘理論,求最優解(即a,b,c,d,e,f)
? 5)根據線性最小二乘理論,求最優解(即a,b,c,d,e,f) 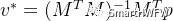 其中
其中 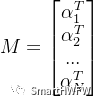 ? ?
? ?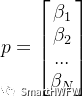 ? 6)計算x0 、y0 、z0 、A、B、C
? 6)計算x0 、y0 、z0 、A、B、C 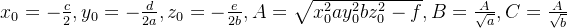 ? 7)校準結果為:
? 7)校準結果為: 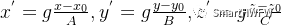
4.C語言實現橢球擬合
01
源碼
02
擬合計算出x0 、y0 、z0 、A、B、C 的值 ? 
01
擬合加速度計的前/后數據對比 


4.橢球擬合校準效果演示
-
陀螺儀
+關注
關注
44文章
784瀏覽量
98717 -
加速度計
+關注
關注
6文章
702瀏覽量
45897 -
模型
+關注
關注
1文章
3244瀏覽量
48844
原文標題:MEMS_慣性傳感器15 - 加速度計校準的橢球擬合方法(基于QMI8658 姿態傳感實現演示)
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
陀螺儀LSM6DSOW開發(2)----上報匿名上位機實現可視化

請問為什么陀螺儀需校準而加速度計不需?
介紹加速度計和陀螺儀的數學模型和基本算法
介紹加速度計和陀螺儀的數學模型和基本算法
三分鐘了解慣性導航系統、加速度計、陀螺儀的工作原理
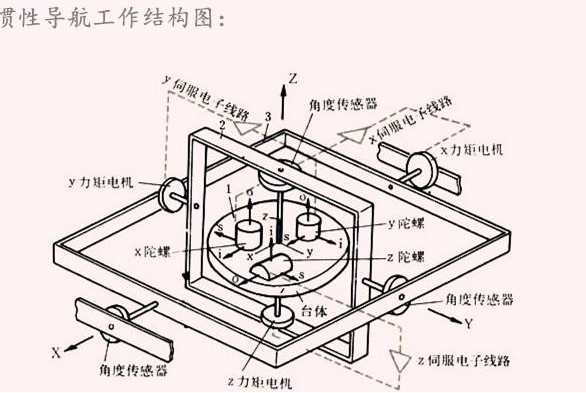
加速度計和陀螺儀的參數意義





 加速度計和陀螺儀的工作原理
加速度計和陀螺儀的工作原理











評論