Razavi教授在他的CMOS模擬IC設計教科書中介紹了米勒補償?shù)膬杉?a href="http://www.xsypw.cn/tags/放大器/" target="_blank">放大器,這是一個很經(jīng)典的結構,里面有很多問題可以分析。可以毫不過分地說,看一個人對模擬IC設計的理解水平,首先就應該問他對兩級放大器的細節(jié)理解程度。
一個初學者通常會有的疑惑是:如何直觀理解兩級放大器采用Rm電阻串接Cc后,零點從右半平面移動到左半平面?
本文旨在解決上述問題,接下來將會做如下兩件事:
①給出一種直觀地判斷兩級放大器零點位置的方法,具體講就是直觀看出零點是左半平面還是右半平面的方法;
②將我們發(fā)展出的零點判定方法使用在其它更復雜的結構上以進一步驗證這種方法。
先說明①
首先必須承認一個事實:若在兩個電壓端點之間存在不止一條路徑,則該電壓傳遞函數(shù)中存在零點。在實際電路設計中,“不止一條路徑”通常指的是兩條路徑。
如果考慮一個五管差分對,會發(fā)現(xiàn)鏡像零點帶來的是左半平面零點(LHPZ)。這是因為五管差分對的差分輸入信號匯聚到輸出有兩條路徑,并且它們最終在輸出是同相疊加的。不可能反相疊加,因為這不符合放大器的定義。那么也就是說,同相疊加的信號路徑將會形成左半平面零點(LHPZ)。
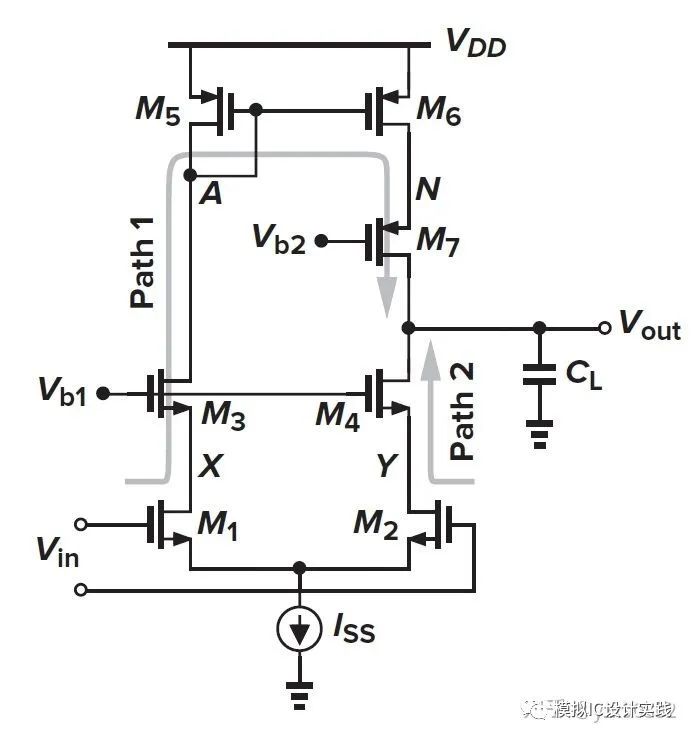
圖1 一個五管差分對以及它的信號路徑
現(xiàn)在考慮米勒補償?shù)膬杉壏糯笃鳎瑔为毧此牡诙壘涂梢苑治龀隽泓c是右半平面的
。這就是我們需要首先分析的問題:如何直觀理解這個右半平面零點?

圖2 一個米勒補償?shù)膬杉壏糯笃?/p>
直觀理解右半平面零點是容易的。考慮高頻下,Cc幾乎將第二級的輸入和輸出短接,原本在低頻下,他們的極性是相反的,但是現(xiàn)在由于短接極性似乎被強迫為同相,這就造成了右平面零點。或許這么講還是不太清楚,再考慮如下例子就會更加清楚:
將第二級的Cc替換成電阻Rm。當Rm=0時,第二級的輸入和輸出被強迫為同相;當Rm= ∞時,輸入輸出被隔離,維持反相。因此中間必然存在一個Rm,使得這種同相反相存在突變點(類似于高中所學的零點存在性定理)。稍微進行電壓增益分析會發(fā)現(xiàn)這個分界點就是 直觀地判斷兩級放大器零點位置
。在這個分界點的左右,就分別對應著左平面和右平面零點。
也就是說,高頻信號同相疊加,則零點為左平面;高頻信號反相疊加,則零點為右平面。目前為止,這個邏輯適合于五管差分對的電流鏡負載和兩級放大器的簡單米勒補償/串聯(lián)電阻補償。因此①的目的達到了。
然后說明②
上面的直觀判斷放大器零點位置的理論應該被更復雜的結構驗證。比如下面的NMC三級放大器,是一個常用的低效率補償結構,我們剛剛發(fā)展出來的的理論也應該適用它。

圖3 一個NMC補償?shù)娜壏糯笃?/p>
根據(jù)我們的理論,首先判斷NMC結構中的雙路結構:分別有紅色和藍色兩組,這對應了開環(huán)傳遞函數(shù)中的兩個零點。注意跨導的符號就是增益的符號,藍色在高頻處為反相疊加;紅色在高頻處為正向疊加。因此藍色代表右平面零點,紅色代表左平面零點,整個放大器的零點為一左一右。

圖4 一個NMC補償?shù)娜壏糯笃鞯男盘柫?/p>
根據(jù)嚴格的分析,三級放大器的傳遞函數(shù)為

可見分子是一個開口向下的二次函數(shù),必然有實根,且一左一右,驗證了我們的理論。那么,是否還能驗證其它的結構呢?
-
CMOS
+關注
關注
58文章
5727瀏覽量
235768 -
放大器
+關注
關注
143文章
13617瀏覽量
213837 -
電阻器
+關注
關注
21文章
3787瀏覽量
62214 -
IC設計
+關注
關注
38文章
1298瀏覽量
104125 -
模擬器
+關注
關注
2文章
879瀏覽量
43294
發(fā)布評論請先 登錄
相關推薦
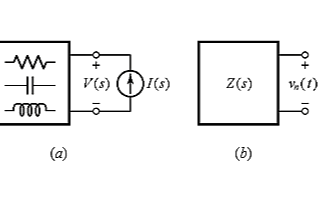
利用電路的自然響應來說明極點和零點位置的影響
兩級功率放大器靜態(tài)偏置點的研究
CMOS兩級運算放大器調(diào)零電路性能分析
利用電路的自然響應說明極點/零點位置的影響




 如何直觀地判斷兩級放大器的零點位置呢?
如何直觀地判斷兩級放大器的零點位置呢?











評論