經典控制理論的特點是以輸入輸出特性（主要是傳遞函數）為系統數學模型，采用頻率響應法和根軌跡法這些圖解分析方法，分析系統性能和設計控制裝置。在實際操作中，確定控制參數也就是這兩個步驟，一是確定系統的開環傳遞函數，二是整定傳遞函數，得到控制參數。

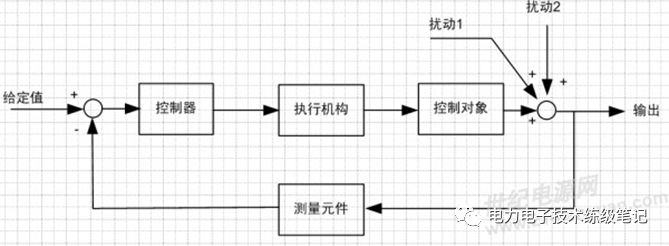
典型的反饋控制系統的框圖

在反饋控制系統中，控制器對被控對象施加的控制作用是取自被控量（即輸出量）的反饋信息，用來不斷地修正被控量與給定值之間的偏差，從而實現對被控對象進行控制任務，這就是反饋控制的原理。

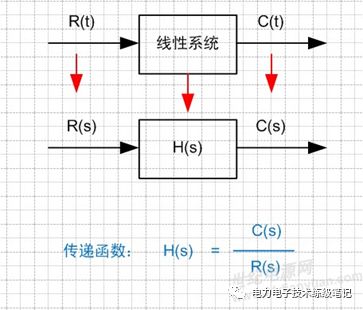
傳遞函數是在頻域里面研究系統特性。頻域里面，只需要幅值、頻率和相位三個信息就能完全確定一個正弦信號。閉環傳遞函數比較復雜，特點不鮮明，同時所有的控制都是負反饋，所以只要開環傳遞函數確定了，閉環傳遞函數的特性也唯一了。

低頻增益就是頻率接近0時（直流分量），幅頻特性的縱坐標值，如下圖的藍色圈所示。這個值決定了閉環系統的穩態精度。對于低頻增益，我們希望越大越好，最好是無窮大。大家所熟知的積分環節，低頻增益就是無窮大，用于消除穩態誤差的。

高頻增益就是頻率比較高的增益，如下圖藍框所示。這一段增益決定了系統抗干擾的能力。大家所熟知的干擾都含有高頻成分。開環傳遞函數對高頻的增益越低，衰減就越大，就不會對系統造成太大的擾動。所以我們希望高頻段能快速降到0db一下，斜率越陡越好。

帶寬就是開環幅頻特性過0db所對應的頻率Wc，也叫截止頻率，如下圖藍框所示。截止頻率越高，代表系統響應速度越快。截止頻率以下，增益大于1，截止頻率以上，增益小于1。也就是說，截止頻率越高，系統能響應的信號頻率也就越高，當然響應速度也就越快了。

相角裕度指的是在截止頻率處，相頻特性對應的相角和-180度之間的距離。相角裕度決定了系統的穩定性。該值越大，系統越穩定。-180度是不穩定的點，這是因為-180度就相當于反向，乘以了-1，就把本身的負反饋變成了正反饋，系統就失穩了。或者可以這么理解閉環傳遞函數為G/(1+G)，可能使分母為零的點是不穩定點，G=-1，必須同時滿足兩個條件：開環傳遞函數的相位為-180°，同時|G|=1。

上面講的都是用波特圖分析系統穩定性的一些基本概念。大家可能更關心的是知道了開環傳遞函數后怎么計算PI參數？這個有很多種辦法，下面介紹按照I型或者II型系統整定方法，需要指出的是，這只是工程中估計PI參數的一種，并非唯一方法。

首先說一下n型系統概念。對于開環傳遞函數，分母中有r個s，就是r型系統。0型系統，分母中沒有s，低頻增益是一個有限值，會有穩態誤差。3型及以上系統很難穩定，因為分母的一個s就是90度響應，多個s相角裕度很快就沒有了。所以常用的就是I型和II型系統。

典型I型系統

I型系統結構簡單，1+Ts為系統本身的一階慣性環節，只需要確定K值即可。該系統的缺點是，對斜坡和加速輸入跟蹤性能差。從bode圖上看，I型系統低頻增益無窮大，沒有穩態誤差。高頻以-40db斜率衰減，抗干擾能力強。截止頻率越高，相角裕度越小；截止頻率越低，相角裕度越大。

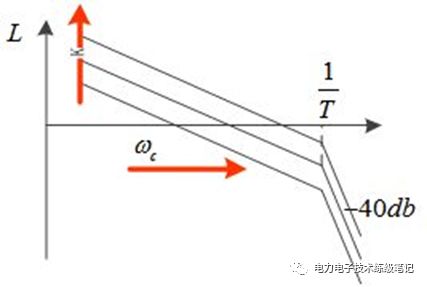
隨著K增大，截止頻率增大，增加了快速性；但降低了相角裕度和抗擾性。在配置中，通常取KT=0.5，來權衡快速性和穩定性。

典型II型系統

II型系統需要確定分子的兩個參數K和τ，分母的1+Ts為系統的一階慣性環節。II型系統對斜坡和加速輸入能無靜差跟蹤。是電力電子控制中最常用的。K和τ有眾多種組合，怎么來合理的確定它們呢？前人們針對II型系統有個中頻帶寬的概念，

確定了中頻寬h，就確定了τ，再改變K使得幅頻特性上下平移，改變ωc。

學者們發現，對于確定的h，存在一個確定的K，使得閉環幅頻特性峰值最小。K和h的關系為：

所以我們的工作就剩下，選擇合適的h就可以了。不同的h有什么影響呢？如下圖所示，h越小，階躍響應越快，但震蕩越多，超調越大；h越大，階躍響應越慢，但震蕩越小，超調越小。大家可以根據自己的需要，選擇不同的h來配置II型系統。