01

—

摘要

分布式聲學傳感(DAS)數據已被廣泛用于監測多裂縫水力壓裂。利用DAS數據解釋水力壓裂幾何形狀（寬度和長度）是當前研究的熱門主題。然而，之前的研究只能從單個低頻DAS (LF-DAS) 數據估計鄰井附近的壓裂寬度。由于多重性問題，沒有人研究從DAS數據表征壓裂長度。本文提出了一個新的模型，從多個數據源（LF-DAS、高頻DAS (HF-DAS) 和注入速率數據）反演出壓裂長度和寬度隨時間的變化。首先，通過對比本井的高頻分布聲學傳感器（HF-DAS）瀑布圖和注入速率曲線，確定注入到每個裂縫中的流體體積。鄰井的低頻分布聲學傳感器（LF-DAS）數據通過Green函數與裂縫寬度關聯起來。通過結合Green函數和流體體積約束，確定裂縫的長度和寬度。

其次，使用Picard方法和最小二乘法來提高模型計算的魯棒性。通過位移不連續方法（DDM）生成的裂縫擴展案例來驗證反演模型。此外，討論了光纖與井眼之間的距離、空間采樣間距、裂縫間距對反演模型計算穩定性的影響。通過結合分布聲學傳感器（DAS）數據和本井或鄰井的其他監測數據（例如，注入速率），可以準確估算出隨時間變化的裂縫長度和寬度。裂縫幾何形狀解釋的結果可以優化壓裂設計，幫助提高生產效率。

02

—

引言

近年來，水力壓裂診斷技術已廣泛應用于非常規油氣藏的開發（Tang and Zhu 2022）。這對于指導壓裂設計和提高生產率至關重要。DAS監測技術是水力壓裂監測的最新研究趨勢之一（Jin and Roy 2017）。DAS監測技術通過井眼沿線的光纖傳遞地下信號，傳感器靠近井眼和儲層，提供了對水力壓裂處理的實時響應。與微地震監測（Rutledge 2004; Warpinski et al. 2004）、壓力/速率瞬態分析（Hu et al. 2022; Ibrahim et al. 2020; Tu et al. 2022）和示蹤數據分析（Karmakar et al. 2016）等傳統監測技術相比，DAS數據更直觀。數據主要用于解釋應變和流動分布。同時，應變和流動分布與壓裂幾何形狀相關，這是評估水力壓裂效果的關鍵指標。因此，DAS監測技術在水力壓裂數據處理過程中對壓裂幾何形狀的解釋具有更大的潛力。

具體而言，根據頻帶范圍，DAS數據可以分為低頻（<1 Hz）和高頻（200–7000 Hz）信號（Tang and Zhu 2022）。與巖石破壞事件相關的LF-DAS數據主要用于應變監測（Li et al. 2020）。光纖周圍的應變變化導致光纖材料變形，這改變了光纖各處的DAS信號振動波形。波形相位與應變有線性關系，這可以定量描述沿光纖物理場擾動位置的應變（Lindsey et al. 2020; Martin et al. 2019）。一些研究人員嘗試通過實地實驗和數值模擬分析LF-DAS應變數據與壓裂幾何形狀之間的關系。

Molenaar 和 Cox (2013)使用沿光纖井的DAS瀑布圖來判斷裂縫是否開啟。Sookprasong等人(2014)觀察了緊密氣井中水力壓裂處理的DAS和分布式溫度傳感監測結果。結合水力壓裂程序，他們發現裂縫的擴展、閉合和重開與DAS數據有很強的相關性。金和羅伊(2017)基于低頻DAS應變和應變速率數據研究了裂縫的開啟和擴展機制。他們利用壓裂作業中來自鄰井的低頻DAS響應的現場實例，證明了低頻DAS數據可用于確定裂縫間距和大小范圍。Sherman等人(2019)模擬了隨機離散裂縫網絡的單一裂縫擴展和相應的合成DAS測量結果，該模擬是由一個包括巖石物理、流體流動和彈性波傳播的多物理程序進行的。Shahri等人(2021)模擬了各種條件下的應變瀑布圖。合成的光纖數據與實際數據非常吻合，顯示出光纖數據與裂縫力學模擬的良好一致性。劉等人(2021a, 2021b)提出了一個基于從DDM演化出的Green函數的反演算法。該算法可以直接從由鄰井監測的低頻DAS應變數據反演裂縫寬度。同時，劉等人(2021c)分析了裂縫高度對裂縫寬度反演結果的敏感性，反演模型由兩個現場案例驗證。唐和朱(2022)開發了一種方法，使用DDM模擬本井的多裂縫擴展和遠場應變速率響應。由于低頻DAS應變數據的一維監測范圍的限制，前面的研究只能定性解釋裂縫擴展或定量計算部分裂縫參數（例如，裂縫寬度）。水力壓裂過程中完整裂縫幾何形狀的動態變化很難僅通過低頻DAS應變數據來反演。

此外，高頻DAS數據與井筒中的流體流動事件有關，主要用于流體分布解釋（Pakhotina等人，2020年）。對于高頻DAS瀑布圖，在裂縫孔位置處提取頻帶（FBE）信號的強度可以定性地確定流體注入的強度。結合相應時間的FBE信號和注入速率數據，可以進一步確定每個射孔簇的流量分布（Pakhotina等人，2020年）。盡管流量分布結果不能直接描述每個裂縫的幾何形狀，但它們可以作為約束條件被納入到Green函數中。因此，低頻DAS應變數據和高頻DAS FBE數據的聯合分析可以解決不同裂縫長度條件下Green函數多解性的問題。此外，原始DAS數據通常以高頻率記錄。可以通過對高頻DAS數據進行降采樣來獲得低頻DAS數據。如果只在本井中安裝光纖，可以從相同的原始DAS數據中獲得高頻DAS和低頻DAS數據，這會很大程度上節省光纖安裝的成本。

本文試圖通過整合Green函數和流動分布函數來開發一種新的水力壓裂反演模型。該模型用于基于DAS數據（即本井的HF-DAS數據和鄰井的LF-DAS數據）和注入速率數據進行壓裂長度和寬度的同時表征，這些數據通常是開源的。首先，對原始DAS數據進行低頻采樣以獲得LF-DAS數據。實測的光纖DAS數據有噪聲。建議使用高保真度濾波算法處理原始數據（如S-G算法），以去除噪聲數據，同時盡可能保留原始數據中的無噪聲有效值。然后，根據DDM發展出的Green函數，將壓裂長度和寬度與鄰井沿線的應變數據相關聯。同時，使用一種動態壓裂網格化方法來表征Green函數的不確定壓裂長度。然后，通過快速傅里葉變換從原始DAS數據中獲得HF-DAS FBE數據。結合HF-DAS FBE和注入速率數據確定相應時間的流動分布。最后，使用流固耦合算法將Green函數和流動分布函數關聯起來。使用Picard方法求解該算法，并確定滿足應變和流動分布條件的壓裂的長度和寬度。通過由正向DDM模型生成的壓裂傳播案例驗證了反演模型。本文還討論了光纖與井筒的距離、空間采樣間距和壓裂間距對反演模型計算穩定性的影響。我們重新推導了一個反向模型，以直接和定量地將光纖數據與時間上的壓裂幾何形狀關聯起來。該模型將常規壓裂數據（例如注入速率）與光纖數據耦合。

03

—

材料與方法

在這一部分，我們推導了一個多裂縫幾何反演模型，主要用于計算裂縫參數（即每個裂縫的長度和寬度）。我們的模型應用了LF-DAS應變數據和HF-DAS FBE數據。

首先，從DDM模型中推導出應變函數，該函數描述了裂縫寬度、裂縫長度和應變之間的關系。井筒、裂縫和光纖的相對位置如圖1所示。根據圖1，有t個垂直裂縫，一個光纖和一個井筒。井筒中的注入速率為Q。光纖與井筒之間的距離為d。離散裂縫之間的間距為df。光纖的空間采樣距離為ds。每個裂縫的長度Lt都有所不同，但所有的裂縫都被劃分為n個裂縫單元。光纖與井筒平行，可以劃分為m個感測點。

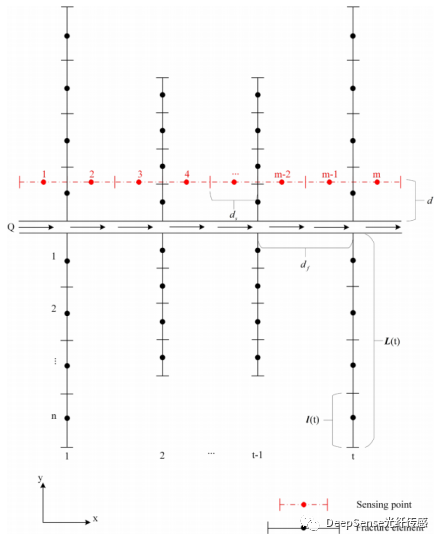
圖1 井筒、裂縫和光纖的示意圖

04

—

模型驗證

這部分通過一個裂縫擴散案例來驗證反演模型。使用DDM模型（Wu 2014）生成這個案例。應變響應是通過劉等人提出的方法（Liu等人，2020；Tang和Zhu，2022）產生的，對應于壓裂時間。對于裂縫生長，擴散準則是最大環向應力準則。

用于模擬的基本參數如表1所示，這些參數來自于吳等人（2017）的案例。我們利用DDM正向模型模擬了表1中的條件下的裂縫擴展。模擬模型的網格包括裂縫網格、光纖網格和層網格。具體來說，層范圍是240×240米，共有3600個網格。光纖總長度為240米，有60個網格，網格大小等于光纖空間采樣距離。裂縫長度和網格大小隨時間變化（最大裂縫長度為150米），有60個網格。圖3顯示了由DDM正向模型模擬的裂縫擴展過程中的壓力和最大裂縫寬度變化。圖4顯示了在裂縫擴展結束時裂縫周圍的位移和應變場。應變可以通過等式3從位移確定。我們在光纖位置分離應變場（圖5a）。結合對應時間的應變場和累積注入，通過反演模型確定裂縫寬度分布。我們比較了DDM正向模型和反演模型在裂縫擴展結束時的裂縫寬度分布（圖5b）。結果顯示，即使在不同的裂縫剖面策略下，反演模型仍然可以通過在光纖位置的有限應變場準確計算裂縫寬度。

表1 用于模型驗證的基本參數

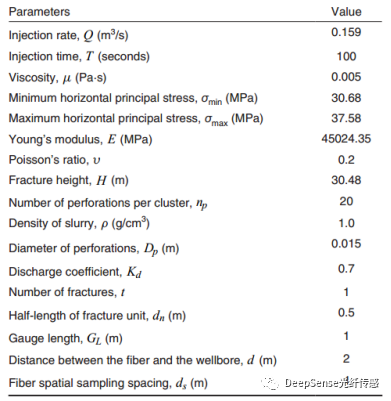
圖3 (a) DDM正演模型模擬的壓力與時間關系。(b) DDM正演模型模擬的最大裂縫寬度隨時間的變化

圖4 (a)裂縫擴展結束時二維位移場，(b)裂縫擴展結束時二維應變場。

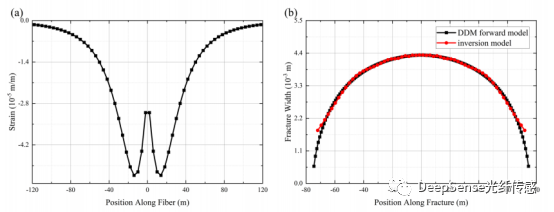
圖5 (a)裂縫擴展末端光纖位置的應變場，(b)采用DDM正演模型和反演模型計算的裂縫寬度分布

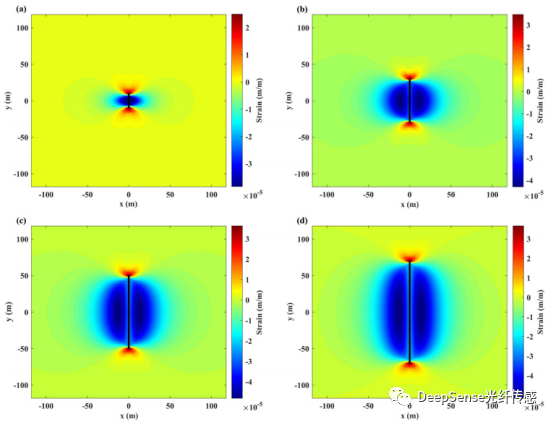
圖62D不同時刻應變場：(a) 9.246秒；(b) 32.862秒；(c) 64.174秒；(d) 98.456秒

此外，我們通過本文的模型確定了每個時間的裂縫的幾何形狀，并與正向模型進行了比較。使用DDM正向模型在每個時間模擬的2D應變場（圖6），我們可以確定光纖位置處的應變的瀑布圖隨時間的變化（圖7）。使用圖7和相應時間的累積注入，可以確定每一時刻的裂縫半長度和寬度。圖8顯示了通過DDM正向和我們的模型確定的所有裂縫半長度和最大裂縫寬度的比較結果。同時，添加了對稱性正則化項，井眼兩翼的裂縫半長度相等，裂縫寬度以井眼為中心對稱分布。結果表明，裂縫半長度和最大裂縫寬度的平均計算誤差分別為1.41和7.47×10?9 m。

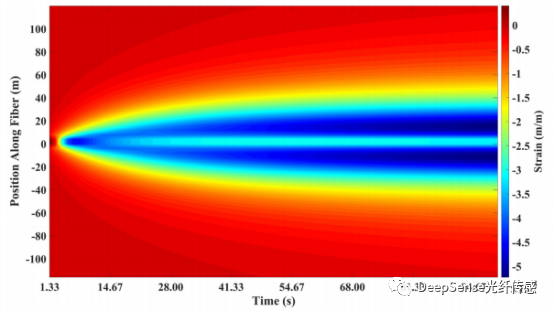
圖7光纖位置應變瀑布隨時間變化圖

與裂縫擴展過程的DDM正向模型相比，反演模型依賴于每次光纖位置的應變數據。此外，反演模型有有限的常數數量的裂縫網格和動態網格長度，使得計算速度更快，收斂更穩定。根據結果的比較，這種動態網格策略的計算精度不會出現大幅偏差。

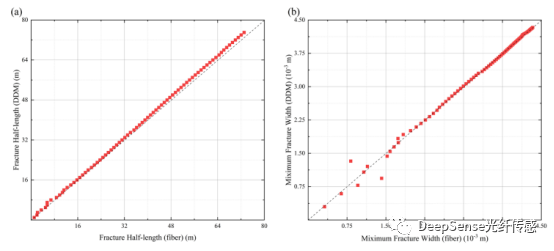
圖8 (a)采用DDM正演模型和反演模型計算的裂縫半長，(b)DDM正演模型與反演模型計算的最大裂縫寬度

05

—

結果和討論

這部分主要討論光纖和井眼之間的距離、空間采樣間隔、和裂縫間距對反演模型計算穩定性的影響。計算的主要參數如表2所示。

表2用于討論的基本參數。

光纖與井眼之間的距離的影響。光纖與井眼之間的距離（d）分別設定為2、14、26和38米。用于計算的主要參數是表2中的情況1。通過DDM正向模型重新模擬得到的相應應變瀑布圖如圖9所示。圖9中，不同光纖位置的應變瀑布圖的"心形"位置不同，這表明裂縫尖端到達光纖的時間不同。使用應變瀑布圖，可以確定傳播過程中的裂縫幾何形狀。

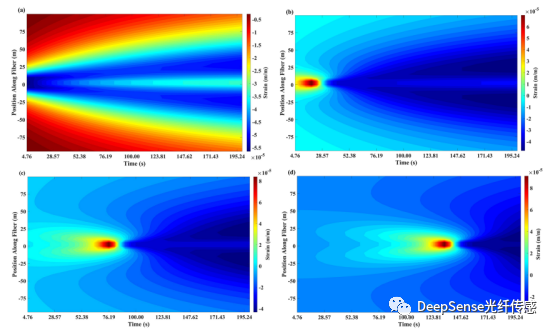
圖9光纖與井筒不同距離處的應變瀑布圖:(a) 2米，(b) 14米，(c) 26米，(d) 38米

為了比較不同距離的計算的穩定性和準確性，反演模型計算的傳播結束時的裂縫半長度和裂縫寬度分布如圖10和圖11所示。圖10展示了反演模型計算裂縫半長度的迭代過程。如圖10所示，裂縫半長度在d為2和26米時收斂最快，而在d為14米時收斂最慢。但模型收斂所需的裂縫半長度的初始值隨著d的增加而增加。光纖的位置影響了裂縫半長度收斂的速度和裂縫半長度的初始范圍。光纖在更遠的距離測量到的應變數據傾向于局部收斂，并且需要更嚴格的迭代初始值。在模擬的情況中，當裂縫半長度的初始值等于或大于光纖距離時，模型的收斂性最好。如圖11所示，由更近的光纖測量到的應變數據能更準確地反演出裂縫寬度分布。但光纖的位置并不影響裂縫寬度反演結果的整體范圍。結果表明，通過光纖沿線的應變數據計算裂縫幾何形狀是受到光纖和井眼之間距離的限制的。劉等人（2021a）已經證明，LF-DAS應變數據可以準確地計算出裂縫碰撞位置的裂縫寬度。除此之外，我們的模型中還增加了本井的HF-DAS數據和注入速率，所有時間和地點的裂縫長度和寬度可以一起計算，通過對裂縫半長度增加嚴格的初始迭代約束，可以改進反演結果。

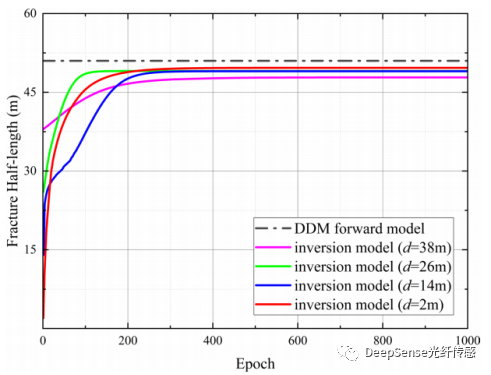
圖10裂縫半長迭代過程

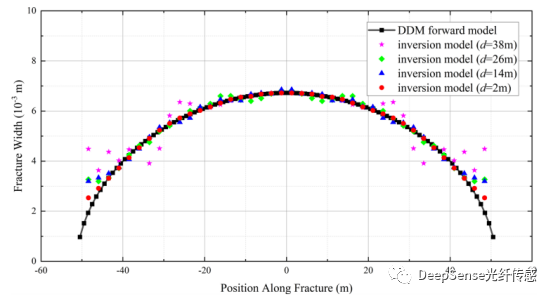
圖11 DDM正演模型與反演模型計算的光纖與井筒不同距離處裂縫寬度分布：(a) 2米，(b) 14米，(c) 26米，(d) 38米

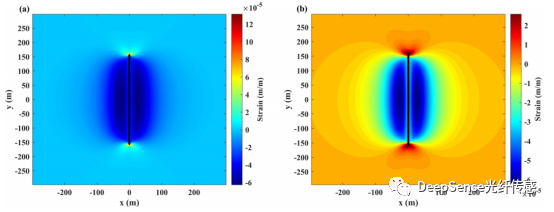
圖122D不同空間采樣間距下的應變場：(a) 2米，(b) 10米

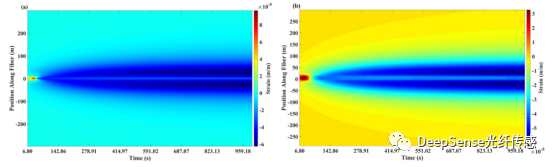
圖13不同空間采樣間距下的應變瀑布圖：(a) 2米，(b) 10米

光纖通常布置在鄰井或本井上。對于鄰井的LF-DAS應變監測，監測距離越遠，應變響應越小。超過一定距離，鄰井的光纖不能監測到應變。模擬案例也表示，對小于鄰井光纖距離的裂縫半長度（裂縫對稱擴散），很難反演出裂縫幾何形狀。因此，需要通過光纖應變瀑布圖的心形位置確定裂縫碰撞位置。使用裂縫碰撞位置作為迭代裂縫半長度的初始值來計算裂縫長度和寬度。對于本井的LF-DAS應變監測，瀑布圖的心形通常不出現，因為光纖與井眼之間的距離為零。因此，模型不需要嚴格的裂縫半長度初始值就可以穩定收斂。

空間采樣間距的影響。光纖空間采樣間距（ds）和標距（GL）是光纖設備的參數，影響了測量的分辨率和數據量級。標距是反演模型的參數之一。因此保持反演模型和光纖設備的測量長度一致，不影響模型計算的準確性。對于空間采樣間距，參考表2中的案例2，分別設置2米和10米的空間采樣間距，反演出場地規模的裂縫幾何形狀。此外，注入時間增加到1000秒，光纖和井眼之間的距離增加到15米。圖12和13顯示了兩種情況的2D應變場和應變瀑布圖，說明了小空間采樣間距的變化更為平滑。特別是，對于圖12的裂縫尖位置和圖13的裂縫碰撞位置，它們附近區域的應變變化顯著。較小的空間采樣間距可以在這些位置確定更大的應變范圍。

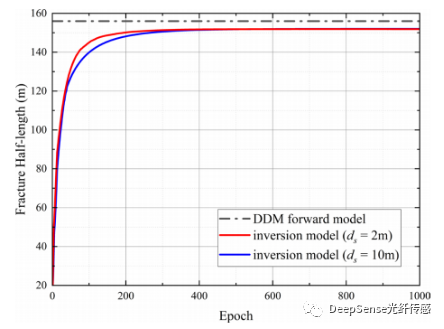
圖14裂縫半長迭代過程

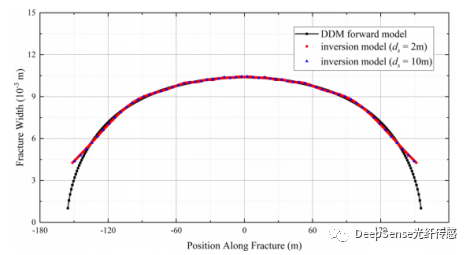
圖15不同空間采樣間距下DDM正演模型和反演模型計算的裂縫寬度分布：(a) 2m，(b) 10m

根據圖14和15所示的計算結果，空間采樣間隔幾乎不影響裂縫幾何形狀計算的穩定性和準確性。結果表示反演模型通常會高估裂縫尖端位置的裂縫寬度，而對最大裂縫寬度的反演相對準確。此外，較小的空間采樣間距需要更長的計算時間。因此，只要在裂縫位置范圍內有足夠的光纖傳感點，使用低分辨率的應變瀑布圖反演裂縫關鍵參數是平衡計算效率和準確性的更好選擇。

裂縫間距的影響。使用四個雙裂縫案例來比較不同裂縫間距對反演模型的影響。裂縫間距(df)分別設定為10，20，30和40米。用于計算的主要參數在表2的案例3中。由DDM正向模型重模擬得到的相應應變瀑布圖在圖16中顯示。計算結果顯示在圖17和18中。小的裂縫間距會產生應力陰影，并模糊兩個裂縫在位移和應變位移中的邊界。同時，隨著裂縫間距的減小，應變瀑布圖趨向于呈現單裂縫特征。在恒定流動分布的情況下，較小的裂縫間距會導致較小的平均裂縫寬度和更大的裂縫長度。光纖在準確位置測得的不同應變數據可用于準確計算裂縫長度和寬度分布。

圖16不同裂縫間距下的應變瀑布圖：(a) 10米，(b) 20米，(c) 30米，(d) 40米

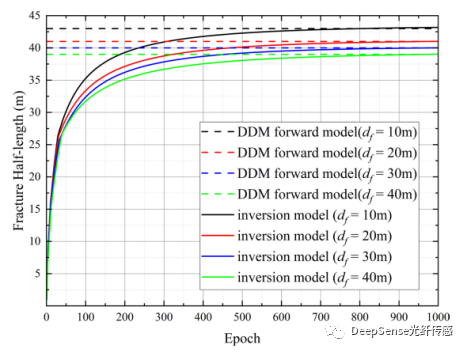
圖17裂縫半長迭代過程

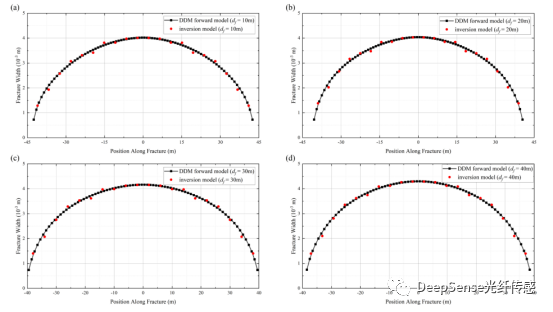
圖18不同裂縫間距下DDM正演模型與反演模型計算的裂縫寬度分布：(a) 10米，(b) 20米，(c) 30米，(d) 40米

06

現場應用

以水力壓裂測試站2（Ciezobka 2021，2022）的一個實地案例來說明模型計算的過程。測試站包括一個垂直導向孔（B5PH）和八個水平井（T13H，T14H，T15H，T16H，B1H，B2H，B3H和B4H）。實地案例來自B1H的第19階段，其遠場應變由部署在B3H上的光纖測量。B1H和B3H是平行且在相同深度的。井間距約為365.76米。裂縫高度約為300米（Wang et al. 2022）。計算的基本參數在表3中。

表3 -用于計算的基本參數

這個部分將通過一個來自水力壓裂試驗站2（Hydraulic Fracturing Test Site 2）（Ciezobka 2021, 2022）的實地案例來說明模型計算的過程。該試驗站包括一個垂直試驗孔（B5PH）和八個水平井（T13H、T14H、T15H、T16H、B1H、B2H、B3H和B4H）。實地案例來源于B1H的第19階段，其遠場應變由部署在B3H的光纖光學測量。B1H和B3H平行且深度相同。井距約為365.76米。裂縫高度約為300米（Wang et al. 2022）。用于計算的基本參數如表3所示。

圖19展示了隨時間在光纖位置的應變瀑布圖。在當前階段有一個裂縫擊中了光纖井(B3H)。通過圖19可以確定裂縫到達B3H的擊中時間為8700秒(Liu et al. 2021d)。我們在裂縫擊中時間計算了沿著光纖的裂縫長度、寬度和應變。圖20a顯示了逆向和真實應變的比較。逆向應變和測量應變可以很好地匹配。應變的平均計算誤差為1.68×10?6m/m。圖20b顯示了裂縫半長度的迭代過程。結果顯示，裂縫在擊中時間到達光纖。與井間距比較，裂縫半長度計算的誤差為4.91米。總的來說，水力壓裂測試站2的實地案例證明了反演模型的穩健性和準確性。

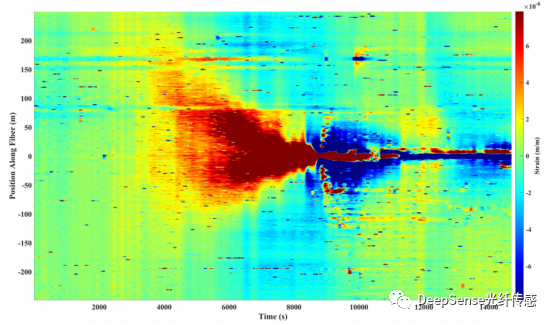
圖19光纖位置應變瀑布圖隨時間變化。

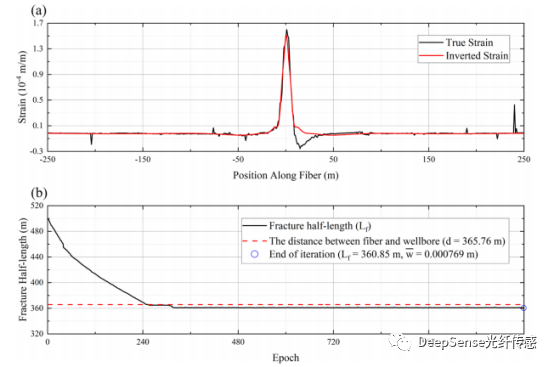
圖20 (a) 8700秒時使用倒寬度的LF-DAS實測應變數據與計算應變數據對比，(b)斷裂半長迭代過程及結果

07

結論

開發了一個基于Green函數和流動分布函數的水力裂縫幾何反演模型。該模型主要利用DAS和注入速率數據來反演裂縫長度和寬度分布。同時，使用流-固耦合算法將Green函數和流動分布函數聯系起來。用Picard方法求解流-固耦合算法。還分析了光纖與井筒之間的距離、空間采樣間距和裂縫間距對算法計算穩定性的影響。這是首次將DAS和注入速率數據結合起來，用于描述裂縫的幾何形狀。

從這項研究中，可以得出以下結論。第一，反演模型將DAS數據、注入速率、裂縫長度和寬度與流體分布函數和Green函數的耦合關聯起來。該方法允許通過在有限的光纖傳感點上的應變穩定反演不同尺度多裂縫幾何形狀。第二，使用遠距離光纖測量的應變數據，可能會導致短裂縫的反演結果不穩定。這是因為DAS應變數據對遠距離的裂縫段不敏感。通過對裂縫半長增加嚴格的初始迭代約束，可以穩定反演過程。第三，光纖的空間采樣間距和標距長度都不影響反演結果的穩定性。但是建議在斷裂位置兩側提供足夠的光纖測點，以提供更多的應變數據。最后，兩個相鄰裂縫的DAS數據呈現出“單裂縫”特征。但裂縫間距不影響反演計算的準確性和穩定性。

反演模型存在以下不足。第一，模型沒有考慮裂縫轉向，裂縫長度的反演結果可能會被低估。第二，測量的應變數據有大量噪聲，這可能導致反演結果不穩定。需要額外的濾波算法來對應變數據進行降噪。第三，反演模型假設裂縫兩翼之間具有對稱性。此外，裂縫模型是2D模型。為適應復雜3D裂縫的反演必須開發更靈活的約束條件。最后，反演模型沒有考慮流體從裂縫到基質的泄露，可能會高估裂縫長度的反演結果。

審核編輯：劉清