1. 原****由
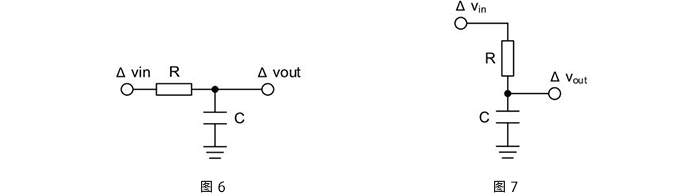
傳遞函數是針對線性時不變(Linear Time-Invariant,LTI)系統定義的,嚴格來說,時變傳遞函數的說法并不十分嚴謹。但 “時變”和“非線性”才是實際系統的本質特性,就拿最簡單的RC電路來說,電阻會隨溫度變化,電容也會隨使用時間發生變化,RC參數的變化就會造成傳遞函數的時變。對于已經建好的傳遞函數,需要分析參數時變的影響時,或者已經建好的某種控制算法,需要驗證對于參數時變的適應能力時,應該如何處理呢?
這時,由線性時不變系統傳遞函數推廣得到的時變傳遞函數是一個不錯的選擇。
2. 方法
2.1 方法一:通過微分方程實現時變傳遞函數
傳遞函數由微分方程通過拉普拉斯(Laplace)變換得到,已知傳遞函數形式后,可以反推出微分方程,再在Simulink中利用基本模塊搭建模型。
如某時變二階系統,其傳遞函數為:
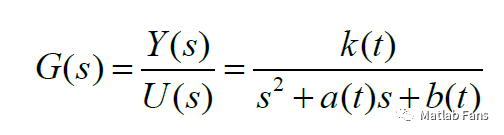
其中,k(t),a(t),b(t)為時變參數。
傳遞函數反推出微分方程為:
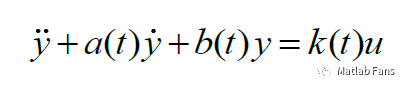
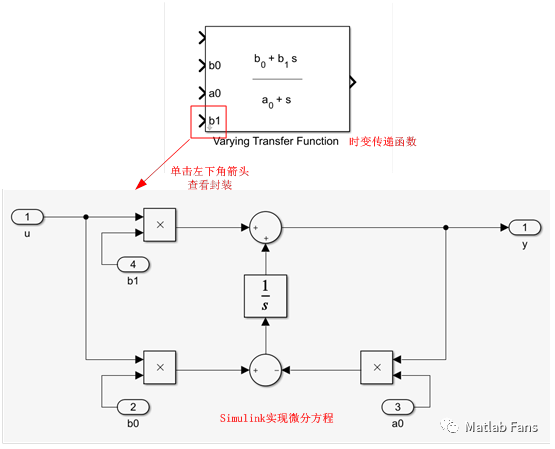
上述微分方程在Simulink中容易搭建:
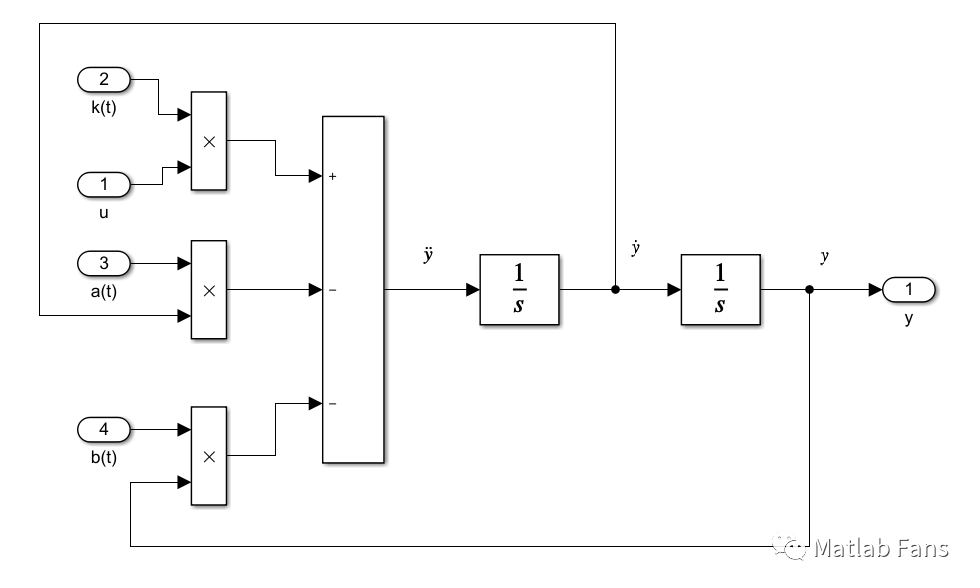
更方便的是,Matlab 2017b之后在控制系統工具箱(Control system toolbox)中推出了時變傳遞函數模塊(Varying Transfer Function),可供用戶直接選用。
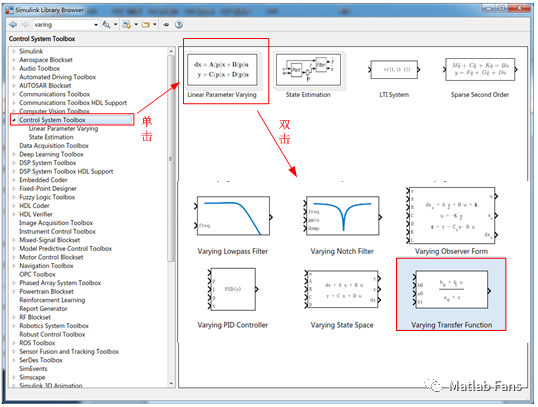
Simulink自帶的這個時變傳遞函數模塊(Varying Transfer Function)就是使用的微分方程方法實現的。
2.2 方法二:通過狀態空間實現時變傳遞函數
傳遞函數還可以轉變為狀態空間形式,如上述二階系統可轉變為可控標準型狀態空間:
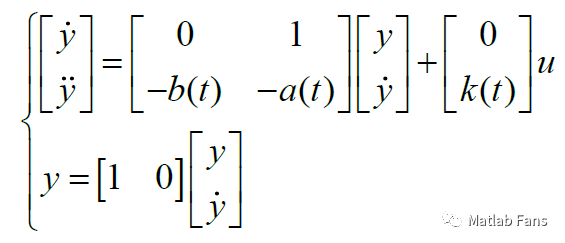
通過上述狀態空間形式也可在Simulink中方便的實現時變傳遞函數。同樣,Matlab 2017b之后在控制系統工具箱(Control system toolbox)中推出了時變狀態空間模塊(Varying State Space),可供用戶直接選用。
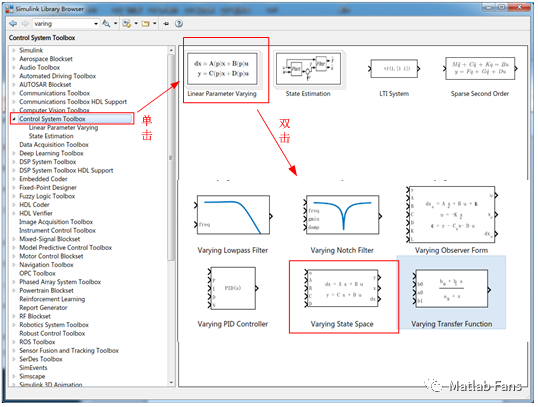
2.3 方法三:通過S函數實現時變傳遞函數
核心思路與方法二相同,即:傳遞函數轉變為狀態空間(可選可控標準型和可觀標準型),通過傳遞函數系數重構狀態空間矩陣,通過狀態空間實現時變傳遞函數。
在Matlab 2017b版本中推出線性時變系統表達方式之前,筆者早年使用Level-2 S函數開發時變傳遞函數模塊,可供Matlab 2017b版本以前的用戶使用 ,也可供需要學習Level-2 S函數使用方法的用戶參考。
2.4 方法四:通過DCP模塊實現時變傳遞函數
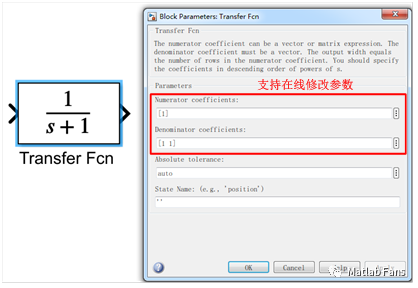
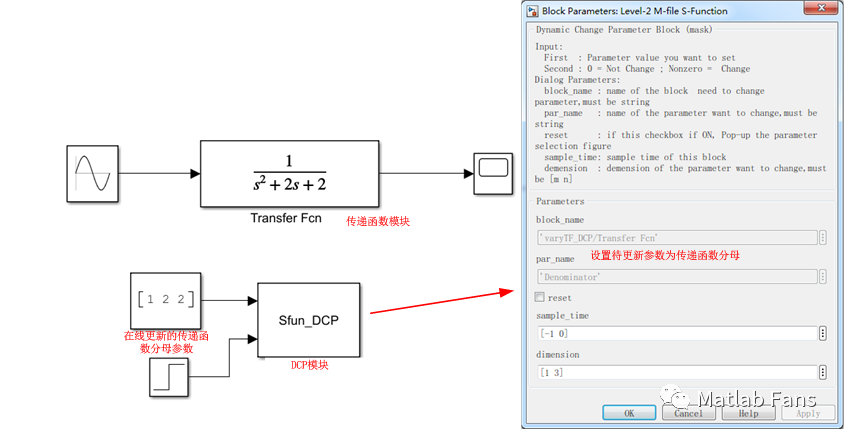
Simulink中的傳遞函數模塊(Transfer Fcn)的分子系數(Numerator coefficients)和分母系數(Denominator coefficients)都支持在線調整,即在仿真過程中可通過set_param函數來在線調整傳遞函數的分子分母系數,由此實現時變傳遞函數。

筆者開發的DCP模塊可實現各類模塊在線更新參數的需求,通過DCP模塊可方便的實現時變傳遞函數。
3. 演示
二階時變傳遞函數:
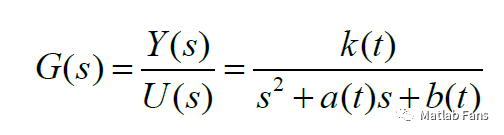
參數時變規律為:
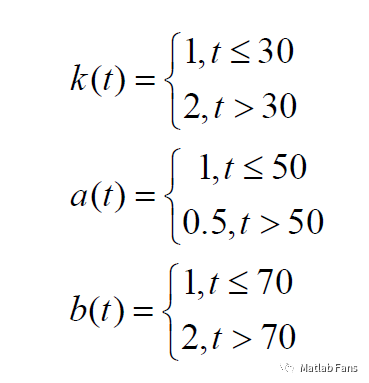
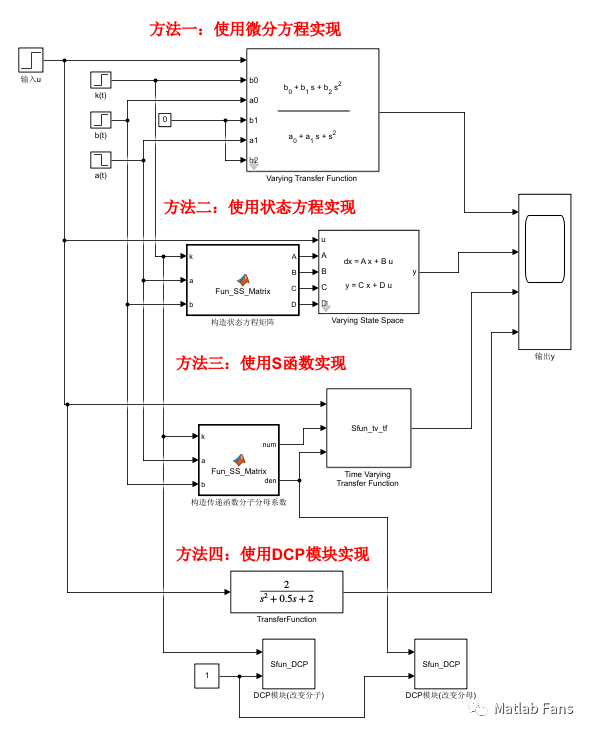
四種方法的Simulink模型:
階躍響應仿真結果:
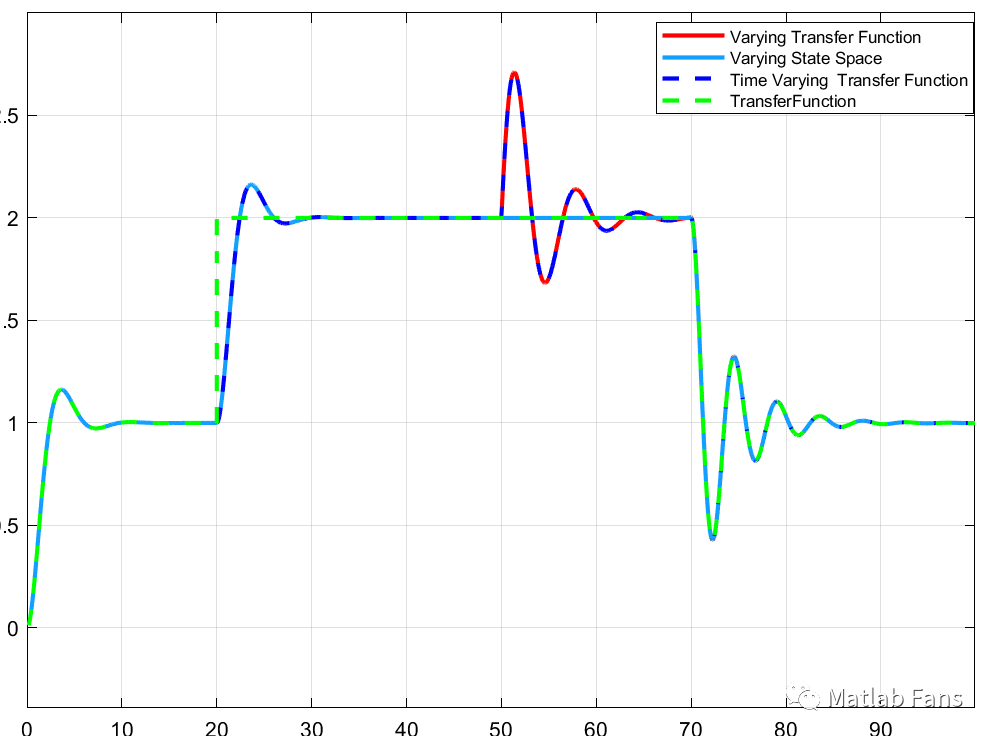
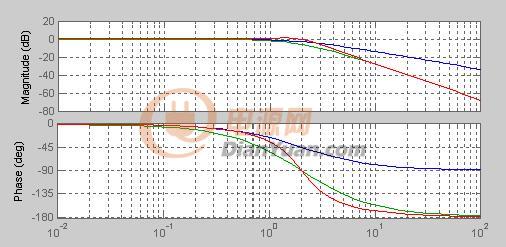
正弦響應仿真結果:
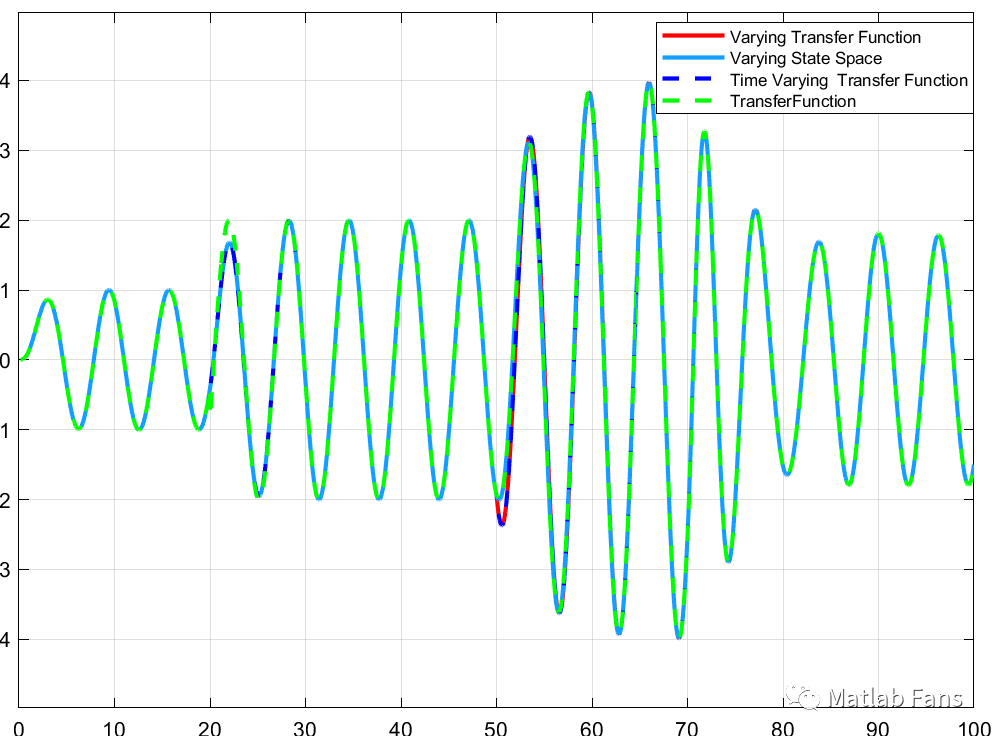
分析仿真結果 :
其主要原因為四種建模方式不同,模型中的記憶環節(如積分環節、狀態量)選取不同,記憶環節與輸出之間的映射關系也不同,因此某些參數變化體現在記憶環節之前的輸入參數中,有些參數變化體現在記憶環節之后的輸出參數中,由此造成突變瞬間動態過程的響應差別,但進入穩態后的響應是相同的。應用中需要根據實際系統的特點靈活選擇實現方式。
-
控制系統
+關注
關注
41文章
6628瀏覽量
110652 -
仿真器
+關注
關注
14文章
1018瀏覽量
83781 -
狀態機
+關注
關注
2文章
492瀏覽量
27554 -
DCP
+關注
關注
0文章
30瀏覽量
17249 -
simulink仿真
+關注
關注
0文章
75瀏覽量
8583
發布評論請先 登錄
相關推薦
模擬電路中傳遞函數的快速列寫方法
基于Butterworth標準傳遞函數設計
傳遞函數的頻率特性




 Simulink中構造時變傳遞函數的四種方法
Simulink中構造時變傳遞函數的四種方法
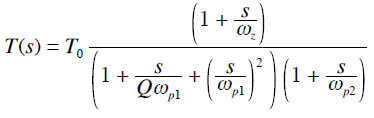
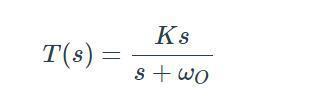










評論