在實際問題中，已知量是數據和數據標簽，決策函數是未知的，即神經網絡的結構未知。

因此，在使用人工神經網絡結構解決實際問題時，需先假設人工神經網絡結構，再將訓練數據輸入到該結構中 ，最后求解待求參數。

一、假設人工神經網絡結構

假設人工神經網絡結構主要需要確定兩個問題：

（1）人工神經網絡結構共有多少層？

（2）每層神經元的數量是多少？

目前，上述兩個問題沒有標準答案，開發人員需根據經驗解決上述兩個問題。解決上述兩個問題時，開發人員可根據以下準則：

（1）若問題是簡單的，兩個類別的分界曲線是不復雜的，則可選用較簡單的人工神經網絡結構，即人工神經網絡層數和每層神經數量均可較少。



圖片來源：中國慕課大學《機器學習概論》

（2）若問題是復雜的，例如：人臉識別問題，則可選用較復雜的人工神經網絡結構，即人工神經網絡層數和每層神經數量均可較多。

（3）若訓練數據較少，則可選用較簡單的人工神經網絡結構。

（4）若訓練數據較多，則可選用較復雜的人工神經網絡結構。

二、求解人工神經網絡待求參數

以兩層神經網絡模型為例，如圖一所示，輸入為(X,Y)，其中，X=[x1,x2]T，Y是標簽值（label），問題為通過改變ω和b的值，使得標簽值Y與實際的人工神經網絡輸出值y最接近。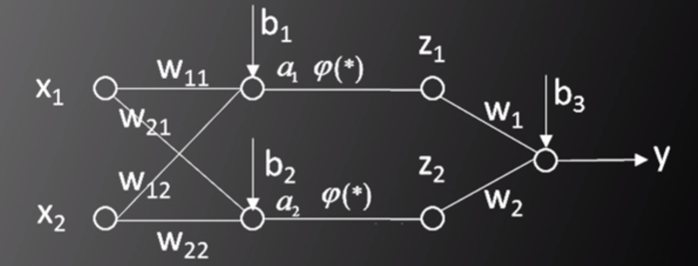



圖一，圖片來源：中國慕課大學《機器學習概論》

根據前篇文章，y的表達式為： y=ω1φ(ω11x1+ω12x2+b1)+ω2φ(ω21x1+ω22x2+b1)+b3

使得y和Y最接近可表達為： Minimize:E(ω,b)=E(X,Y)[(Y-y)2]

其中，E(X,Y)為訓練樣本和標簽的數學期望（平均值）。因為y是(ω,b)的非凸函數，所以該問題無法求得唯一最小值。

因此，采用梯度下降法(Gradient Descent Method)求解局部極小值。梯度下降法的步驟如下：

（1）隨機選取ω和b的初始值(ω(0),b(0))

（2）應用迭代算法求目標函數的局部極值，在第n步迭代中，ω和b的迭代公式為： ω(n+1)=ω(n)-α·?E/?ω b(n+1)=b(n)-α·?E/?b

其中，α為學習率（Learning rate），α由開發人員設定，開發人員需選取合適的α值，若α值被設定得過大，則容易錯過局部極值點，若α值被設定得過小，則可能較長時間不能找到局部極值點，只有當α值被設定得合適時，才能快速收斂至局部極值點。但因為人工神經網絡對應的決策函數未知，所以沒有一種可求解α值的方法，開發人員需根據經驗設定α值。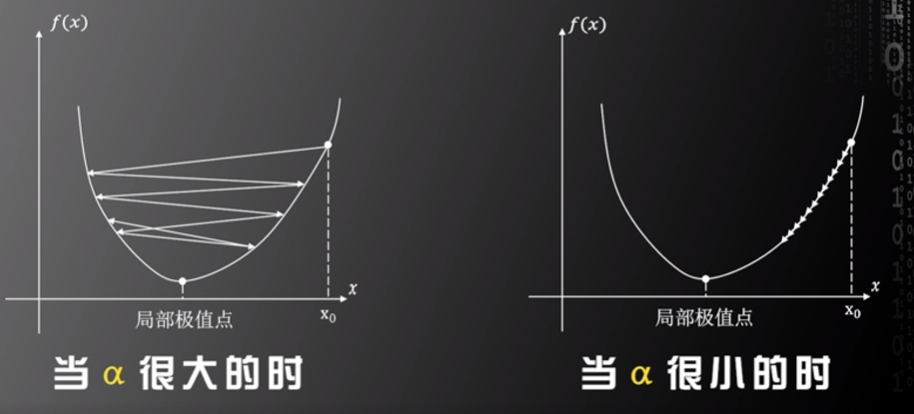



圖片來源：中國慕課大學《機器學習概論》

梯度下降法的含義：如圖二所示，通過迭代的方式逐步遍歷x1，x2，x3，…，xn，最終找到函數的局部極小值，此值即為y和Y最接近的值。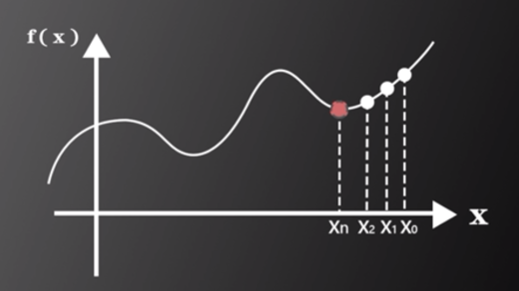



圖片來源：中國慕課大學《機器學習概論》

審核編輯：劉清