一、DFT、DCT和DWT的概述
1.1 DFT與FFT簡介
DFT(Discrete Fourier Transform)代表著離散傅里葉變換,是作為有限長序列的在數(shù)字信號(hào)處理中被廣泛使用的一種頻域表示方法,。DFT來源于傅里葉變換(FT)和周期序列的離散傅里葉級(jí)數(shù)(DFS),DFS是一種適用于周期序列的變換。但由于實(shí)際的數(shù)字信號(hào)處理的過程中獲取和處理的序列是有限長的序列,而周期序列作為一種理論上的模型實(shí)際上只有有限個(gè)序列值才具有意義,而且它和有限長序列有著本質(zhì)上的聯(lián)系。因此可以從周期序列的離散傅里葉級(jí)數(shù)(DFS)出發(fā)推導(dǎo)出有限長序列的離散頻譜表達(dá)式(DFT)。可以將DFT所要變換的對(duì)象——有限長序列看成是周期序列的一個(gè)周期表示,即先把序列值周期延拓后再取主值序列后即可得到有限長序列。從而可以推斷出DFT和IDFT的變換式為:
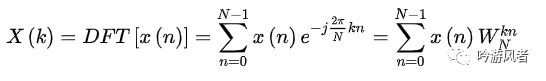
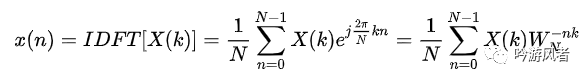
同時(shí)x(n)的N點(diǎn)DFT也是其傅里葉變換在區(qū)間[0,2π]上的N點(diǎn)等間隔采樣,因此與傅里葉變換(FT)也關(guān)系密切。一般情況下,信號(hào)序列x(n)及其頻譜序列都是用復(fù)數(shù)來表示的,因此計(jì)算DFT的一個(gè)值X(k)需要進(jìn)行N次復(fù)數(shù)乘法和N-1次復(fù)數(shù)加法。這就說明直接計(jì)算N點(diǎn)的DFT需要進(jìn)行N2次復(fù)數(shù)乘法以及N(N-1)次復(fù)數(shù)加法,IDFT亦是如此。因此,DFT與IDFT的運(yùn)算次數(shù)與N2成正比,隨著N的增加,運(yùn)算量將急劇增加。
為了減少DFT的計(jì)算量從而快速的得到變換之后的結(jié)果,研究人員發(fā)明了一種算法——FFT算法。FFT算法將時(shí)域序列逐次分解為一組子序列,利用旋轉(zhuǎn)因子的特性由子序列的DFT來實(shí)現(xiàn)整個(gè)序列的DFT。DIT-FFT算法的原理是通過將原始有限長序列不斷進(jìn)行奇偶分解成2M個(gè)DFT,再利用旋轉(zhuǎn)因子的特性和DFT的隱含周期性將計(jì)算量縮短。因此N=2M的序列經(jīng)過M級(jí)時(shí)域奇偶抽取可分解為N個(gè)1點(diǎn)DFT(即時(shí)域序列本身)和M級(jí)蝶形運(yùn)算,其中每一級(jí)蝶形運(yùn)算有N/2個(gè)蝶形,含N/2次復(fù)乘和N次復(fù)加。通過計(jì)算可以得到總運(yùn)算量為 次復(fù)乘和 次復(fù)加。FFT算法比直接計(jì)算DFT的運(yùn)算量大大減少,尤其是N較大時(shí),計(jì)算量的減少更為顯著。比如,當(dāng)N=1024時(shí),采用FFT算法時(shí)復(fù)數(shù)乘法的次數(shù)低于直接DFT時(shí)的次數(shù)的千分之五。
1.2 DCT簡介
DCT為離散余弦變換,是在DFT的基礎(chǔ)上推導(dǎo)出來的,是DFT的一種特殊形式。在DFT傅立葉級(jí)數(shù)展開式中,如果被展開的函數(shù)是實(shí)偶函數(shù),那么其傅立葉級(jí)數(shù)就只包含余弦項(xiàng),再將其離散化(DFT)可導(dǎo)出該余弦項(xiàng)的余弦變換就是離散余弦變換(DCT)。離散余弦變換被展開的函數(shù)是實(shí)偶函數(shù),因此離散余弦變換相當(dāng)于一個(gè)長度是其本身兩倍的離散傅里葉變換,并且離散余弦變換后的函數(shù)仍然為一個(gè)實(shí)偶函數(shù)。一維的DCT變換公式如下:
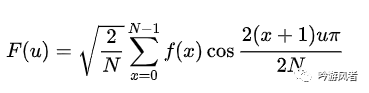
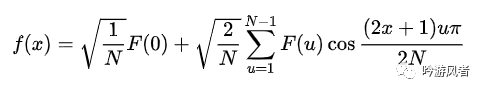
對(duì)于圖像這類的二維離散序列A來說,它的二維離散余弦變換定義如下所示:
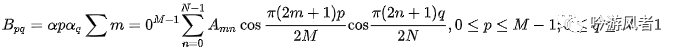
其中B的值被稱為矩陣A的DCT系數(shù),在得到所有的DCT系數(shù)后,便形成了一個(gè)與A同樣大小的矩陣B。通過下面的反離散余弦變換公式,可以由矩陣B恢復(fù)原來的離散序列A:
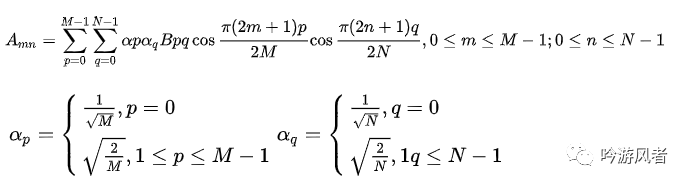
1.3 DWT簡介
DWT(Discrete Wavelet Transformation)代表著離散小波變換,是對(duì)基本小波的尺度和平移進(jìn)行離散化的一種新型譜分析工具。它既能過考察考察局部時(shí)域過程的頻域特征,又能考察局部頻域過程的時(shí)域特征,因此即使是那些非平穩(wěn)過程能夠進(jìn)行很好的變換和處理。對(duì)于圖像來說,它能夠?qū)D像變換為一系列的小波系數(shù)并將這些系數(shù)進(jìn)行高效的壓縮和儲(chǔ)存,并且小波的粗略邊緣消除了DCT壓縮普遍具有的方塊效應(yīng)從而可以更好地還原和表現(xiàn)圖像。
在數(shù)字圖像處理的過程中需要將連續(xù)的小波及小波變換進(jìn)行離散化。一般計(jì)算機(jī)是二進(jìn)制運(yùn)算和處理的,因此使用計(jì)算機(jī)進(jìn)行小波變換的實(shí)現(xiàn)需要進(jìn)行二進(jìn)制離散處理。這種離散化的小波及其相應(yīng)的小波變換稱為離散小波變換。實(shí)際上,離散小波變換是對(duì)連續(xù)小波變換的尺度、位移按照2的冪次進(jìn)行離散化得到的,因此也被稱為二進(jìn)制小波變換。雖然經(jīng)典的傅里葉變換能夠反映出信號(hào)的全局及整體信息,但其表現(xiàn)形式卻不夠直觀,并且信號(hào)頻譜易受噪聲信息的干擾從而復(fù)雜化。因此需要使用一系列的帶通濾波器將信號(hào)分解為不同的頻率分量并對(duì)這些頻率子帶進(jìn)行分開處理。而小波分解的好處就在于它能夠在不同的尺度上對(duì)信號(hào)進(jìn)行分解,可以根據(jù)不同的用途及目標(biāo)選擇不同的尺度來獲得想要的頻域信息。
對(duì)于很多信號(hào)來說,其低頻分量常常蘊(yùn)藏在信號(hào)的基本特征,而高頻信號(hào)只是給出了信號(hào)的細(xì)節(jié)信息,如圖像信號(hào)的邊緣輪廓信息。語音信號(hào)如果去掉了高頻信號(hào)仍能聽出所承載信息的基本內(nèi)容,盡管聲音聽起來和以前可能不同;如果去掉信號(hào)的低頻部分,則聽到的是一些沒有意義的聲音。因此我們可以有選擇的丟棄掉高頻信息以達(dá)到有損壓縮信號(hào)的目的。在小波分析中經(jīng)常將信號(hào)分解為近似部分和細(xì)節(jié)部分,其中近似部分表示信號(hào)的低頻信息;細(xì)節(jié)部分代表著信號(hào)的高頻信息。因此原始信號(hào)通過兩個(gè)相互的濾波器產(chǎn)生兩個(gè)信號(hào)。通過不斷的分解可以將近似信號(hào)連續(xù)分解成許多低分辨率的信號(hào)成分直到達(dá)到想要的目標(biāo)。因此在實(shí)際的應(yīng)用中,一般根據(jù)信號(hào)的特征或者合適的標(biāo)準(zhǔn)來選擇適當(dāng)?shù)姆纸鈱訑?shù)。
對(duì)于一個(gè)二維平面的任意函數(shù) 來說,其連續(xù)的小波變換為:
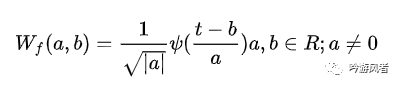
其重構(gòu)公式(逆變換)為:
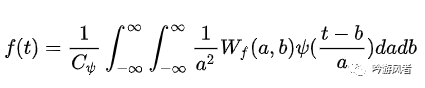
離散小波變換需要將連續(xù)小波變換中的尺度參數(shù)a和平移參數(shù)b平移參數(shù)b進(jìn)行離散化。因此可以得到相應(yīng)的離散小波變換為:
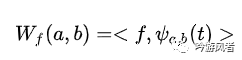
其重構(gòu)公式為:
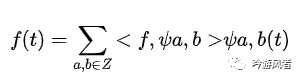
二、DFT、DCT和DWT的聯(lián)系和區(qū)別
2.1 聯(lián)系
這三種變換都是通過將空間域上的圖像信號(hào)轉(zhuǎn)換到頻域中,然后在將圖像的頻域分解各個(gè)子帶并對(duì)各個(gè)子帶進(jìn)行分析以得到想要的圖像信息。其中DCT是DFT的一種特殊的形式,若被展開的函數(shù)是實(shí)偶函數(shù),則其傅立葉級(jí)數(shù)中只包含余弦項(xiàng),再將其離散化(DFT)就可導(dǎo)出DCT。因此DCT屬于DFT 的一個(gè)子集,它們都是對(duì)信號(hào)的整體進(jìn)行分析變換。而DCT和DWT的聯(lián)系在于圖像信號(hào)經(jīng)過這兩種變換之后的基本信息都集中于左上角,因此都可以只保留左上角的數(shù)據(jù)而刪除其他數(shù)據(jù)并很好的還原回原始數(shù)據(jù)從而能進(jìn)行圖像壓縮(見圖1)。
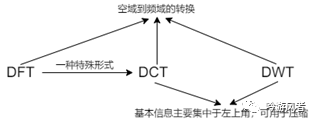
圖1 DFT、DCT和DWT的聯(lián)系示意圖
2.2 區(qū)別
從上文可知DCT是DFT的一種特殊的形式,DCT是對(duì)實(shí)偶函數(shù)進(jìn)行轉(zhuǎn)換的,它相當(dāng)于一個(gè)長度大概是其兩倍的傅里葉變換,并且變換之后得到的函數(shù)仍然是實(shí)偶函數(shù)。在圖像處理的運(yùn)用方面,DFT主要用于去除雜質(zhì)成分對(duì)圖像造成的干擾,如圖像去噪等。圖像經(jīng)過離散傅里葉變換之后從時(shí)域信息變成了頻域信息進(jìn)而分為高頻部分和低頻部分,對(duì)高頻噪聲進(jìn)行濾波即可去除掉在時(shí)域中難以區(qū)分的噪聲及雜質(zhì)成分。DCT則主要用于圖像的壓縮。圖像經(jīng)過離散余弦變換后其基本信息主要集中在左上角,因此可以去除除左上角之外的其他數(shù)據(jù)也能很好的將圖像復(fù)原成原始的樣子,因此能夠在誤差可接受的范圍內(nèi)將圖像進(jìn)行壓縮儲(chǔ)存。DWT和DCT的區(qū)別在于圖像進(jìn)行DWT變換后其小波域分為四個(gè)子帶,每個(gè)子帶不僅包括圖像的頻域成分還包括其空域成分。并且其包含圖像主要信息的左上角子帶(LL子帶)能夠再次不斷的進(jìn)行DWT變換從而將其連續(xù)分解成許多不同分辨率的信號(hào)成分(見圖2),這意味著我們可以通過控制小波變換的層數(shù)來實(shí)現(xiàn)不同的壓縮率目標(biāo)。

圖2 連續(xù)DWT變換示意圖
從圖3中我們可以看到盡管原始圖像經(jīng)過了多次小波變換,其基本的圖像信息仍然集中在左上角的LL子帶。因此雖然其圖像的分辨率成指數(shù)級(jí)下降,我們還是可以使用各個(gè)層級(jí)的LL子帶的數(shù)據(jù)恢復(fù)出原始的圖像從而達(dá)到基本恢復(fù)圖像的前提下各種壓縮比的要求。

圖3 三次haar小波變換后生成的圖像
-
小波變換
+關(guān)注
關(guān)注
2文章
183瀏覽量
29783 -
DCT
+關(guān)注
關(guān)注
1文章
56瀏覽量
19891 -
DWT
+關(guān)注
關(guān)注
0文章
20瀏覽量
11154 -
數(shù)字信號(hào)處理器
+關(guān)注
關(guān)注
5文章
470瀏覽量
27375 -
DFT算法
+關(guān)注
關(guān)注
0文章
27瀏覽量
7555
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦




 DFT、DCT和DWT之間有何聯(lián)系呢?其區(qū)別在哪?
DFT、DCT和DWT之間有何聯(lián)系呢?其區(qū)別在哪?










評(píng)論