做控制時，大家經常會有這樣的感受“代碼很豐滿，現實很骨感”，這是因為將計算機指令轉移到實際硬件時，由于物體的慣性以及各種非理想化的因素影響，往往會出現實際與預期不符合的情況。

這篇文章將以“操控遙控飛機從地面飛到10米高度并懸停”為例子，用最通俗易懂的方式，讓你理解PID。在這個問題中，我們假設加速度是可以直接調控的（實際生活中往往也是這樣），因此，我們輸入的量為加速度的大小和方向（正負），而我們最終想要得到的結果就是高度穩定在10米。

首先我們來講控制方法：

控制方法主要分為“開環控制”和“閉環控制”，這兩種控制方法的簡單理解為：

開環控制：計算出飛機從地面到10米高度所需要的加速度以及作用時間，然后將其編寫為一條固定的指令，“一次執行，全過程受益”。

閉環控制：在飛機飛行的過程中，系統時刻關注飛機的狀態，并做出相應的調整。而PID控制就是最常用的閉環控制。

PID原理

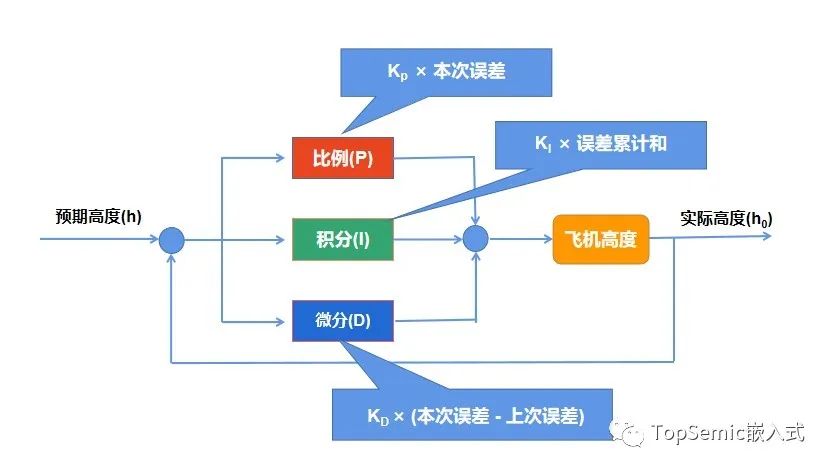
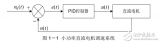
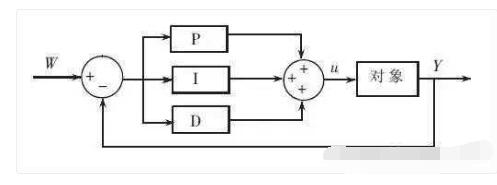
一講到原理，很多人都會搬出PID公式，數學較好或者學過自控的人還好，要是遇見一個半路轉行做控制的，看見“微分”和“積分”，頭都大了。其實，由于生活中信號采樣具有一定的間隔，因此我們經常遇見的都是離散信號的控制，只需要讀懂下圖即可：

實踐出真知(python實現PID)

3.1 導入包

`importtime`

`importmatplotlib.pyplotasplt`

3.2 PID實現

#實現一個PID控制器
classPIDController:

def__init__(self,kp,ki,kd):

"""

初始化PID控制器

參數:

kp(float):比例系數

ki(float):積分系數

kd(float):微分系數

"""

self.kp=kp#比例系數

self.ki=ki#積分系數

self.kd=kd#微分系數

self.prev_error=0#上一次的誤差

self.integral=0#誤差積分值

defcalculate(self,setpoint,current_value):

"""

計算PID控制器的輸出

參數:

setpoint(float):設定值（目標值）

current_value(float):當前值（被控制的系統當前狀態）

返回:

output(float):控制器的輸出

"""

error=setpoint-current_value#計算誤差

self.integral+=error#更新誤差積分

derivative=error-self.prev_error#計算誤差導數

output=self.kp*error+self.ki*self.integral+self.kd*derivative

#計算控制輸出，包括比例、積分和微分部分

self.prev_error=error#保存當前誤差作為下一步的上一次誤差

returnoutput#返回控制器的輸出

3.3 飛行器模擬

#飛行器模擬
classAircraftSimulator:

def__init__(self):

self.height=0#飛行器初始高度為0

self.velocity=0#飛行器初始速度為0

defupdate(self,throttle,time_step):

"""

更新飛行器狀態：高度和速度

參數:

throttle(float):油門輸入，控制引擎輸出的力量

time_step(float):時間步長，模擬器更新的時間間隔

"""

acceleration=throttle-0.1*self.velocity

#根據簡化的動力模型計算飛行器的加速度

#加速度等于油門輸入減去速度的一部分，這是簡化的模型

self.velocity+=acceleration*time_step

#根據加速度更新速度

#新速度等于當前速度加上加速度乘以時間步長

self.height+=self.velocity*time_step

#根據速度更新飛行器的高度

#新高度等于當前高度加上速度乘以時間步長

3.4 主函數與繪圖

#主函數

defmain():

#PID參數

kp=5.0

ki=0.1

kd=10

#初始化PID控制器和飛行器模擬

pid_controller=PIDController(kp,ki,kd)

aircraft_simulator=AircraftSimulator()

target_height=10.0

time_step=0.1

total_time=20#總模擬時間增加到20秒

current_time=0.0

#存儲時間和高度數據的列表

time_data=[]

height_data=[]

#模擬循環

whilecurrent_time

	

	實驗與參數理解

	PID的控制經常會涉及到KP、KI、KD三個參數的調節，如果盲目調節則會花較長時間，接下來我們將用直觀實驗來理解以下幾個參數的具體含義。

	4.1 比例環節

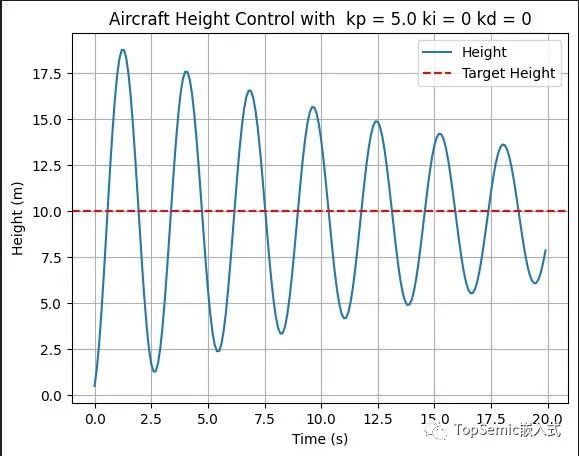
	計算公式為KP × 誤差，具體的含義即為誤差越大，值越大。這一點是非常直觀的，誤差越大則說明偏離預期值越遠，我們要加大“油門”，快速調整！以下是當KI、KD為0，只有KP=5的測試結果：

	

	從圖中我們可以看到雖然慢慢的想10收斂，但由于誤差越大，其“油門”越大，就像是一個“莽夫”，盡管每次都在調整，但總是用力過猛！

	4.2 微分環節

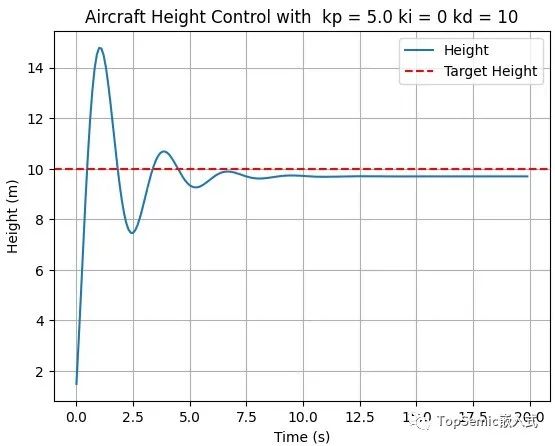
	計算公式為KD × (本次誤差 - 上次誤差)，對于這個公式，我們可以理解為用來中和“用力過猛”。以下是當KP=5、KD=10、KI=0的測試結果：

	

	顯然，這個結果要比上次好很多，但始終低于10，這是因為我們在模擬中加入了一個干擾條件：

	
#添加擾動

disturbance=-1.5

control_signal+=disturbance


	

	因此，要想消除這個干擾，就需要積分環節的加入。

	4.3 積分環節

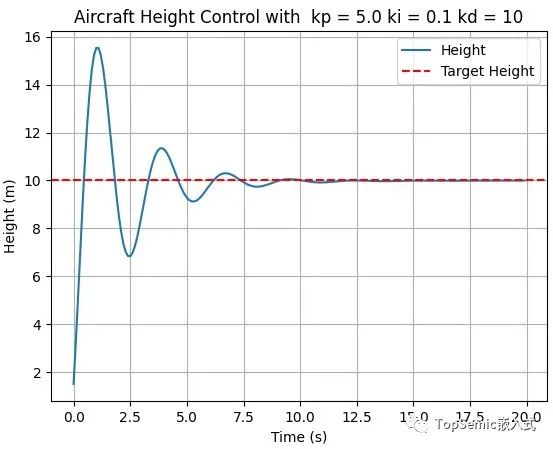
	積分環節的公式為KI × 誤差累計和，用官方的語言來說，用來調整“穩態誤差”，其實，所謂的穩態誤差就可以理解為“一直存在的誤差”，也就是在本次實驗中加入的持續干擾！以下是當KP=5、KD=10、KI=0.1的測試結果：

	

	從這次的測試中，我們看出，得到了幾乎完美的結果！

	總結

	對于PID參數調節，認準3個點：

	P:大力出奇跡

	I：消除持續存在的誤差

	D：“中和”用力過猛，減少波動

	    責任編輯：彭菁