曲線是數學中的一個基本概念，它可以定義為一種平滑的、連續的、無限延展的函數圖像。在平面直角坐標系中，曲線通常由函數y=f(x)表示，其中x和y是變量，而f是函數關系。

切點是指曲線上的一個點，在該點處曲線的切線存在且垂直于該點處的切線。換句話說，切點是曲線在該點處的斜率等于該點處切線的斜率。

在數學中，通常使用導數來找到曲線在某一點的切線，它可以用于計算函數圖像上某一點處的斜率。因此，為了找到曲線在某一點的切線，首先需要計算該點處的導數，然后找到與該導數相對應的x和y值。這些值就是切點。

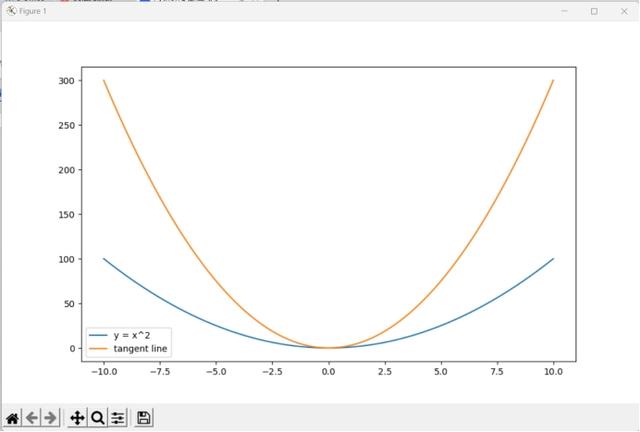
以下是一段使用Python的matplotlib庫繪制曲線并計算切線的示例代碼。這個例子會繪制一個簡單的二次函數（比如y = x^2）的圖像，然后在其上一點計算切線。

import numpy as np

import matplotlib.pyplot as plt

定義二次函數

def f(x):

return x**2

定義導函數

def df(x):

return 2*x

生成x的值

x = np.linspace(-10, 10, 400)

計算y的值

y = f(x)

計算切線的斜率

dx = 0.01 # 這是x的增量，可以根據需要進行調整

dy_dx = (f(x + dx) - f(x)) / dx # 根據定義，斜率等于函數值的增量除以x的增量

繪制原始函數圖像

plt.figure(figsize=(10, 6))

plt.plot(x, y, label='y = x^2')

繪制切線

plt.plot(x, y + dy_dx*x, label='tangent line')

添加圖例

plt.legend()

顯示圖像

plt.show()

這段代碼首先定義了一個二次函數f(x) = x^2和它的導函數df(x) = 2*x。然后，使用numpy得linspace函數生成了一組從-10到10的等間隔的x值，并根據這些x值計算對應的y值。

然后，通過改變x的值（增量為dx）并計算函數值的增量，來計算切線的斜率。最后，使用matplotlib得plot函數來繪制原始的二次函數和切線，并通過show函數顯示圖像。