Guava BloomFilter

布隆過濾器是一個(gè)很長的二進(jìn)制向量和一系列隨機(jī)映射函數(shù)。布隆過濾器可以用于檢索一個(gè)元素是否在一個(gè)集合中。它的優(yōu)點(diǎn)是空間效率和查詢時(shí)間都比一般的算法要好的多，缺點(diǎn)是有一定的誤識(shí)別率和刪除困難。

基本概念

當(dāng)需要判斷某個(gè)元素是否在某個(gè)數(shù)據(jù)集中時(shí)，一般會(huì)怎么做？

1. 將數(shù)據(jù)集封裝成集合，比如List、Set等
2. 通過集合提供的API判斷該元素是否存在于集合

這樣的實(shí)現(xiàn)比較簡單，同時(shí)通過現(xiàn)有的JDK都能很快達(dá)到目的，但是設(shè)想一下，如果上面說到的集合數(shù)據(jù)量非常的大，這樣不僅會(huì)耗費(fèi)較大的存儲(chǔ)空間，同時(shí) 在集合中檢索元素的時(shí)間復(fù)雜度也會(huì)隨之增加。那么有沒比較好的方法去實(shí)現(xiàn)判斷元素是否存在這樣的情形呢？

也就是 布隆過濾器 。

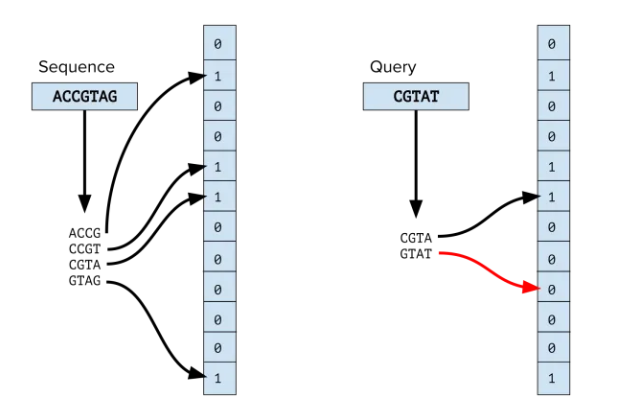
通過一系列的Hash函數(shù)將元素映射到一個(gè)位陣列（Bit Array）中的多個(gè)點(diǎn)位上，判斷元素是否存在，則是判斷所有點(diǎn)位是不是都為1。然而，位陣列上都為1并不一定能夠保證該元素一定存在，也有可能是其他元素Hash后落在了該點(diǎn)位上，這就是布隆過濾器的誤判。

因此通過布隆過濾器我們可以確定：

1. 元素可能在集合中
2. 元素一定不在集合中

應(yīng)用場(chǎng)景

• 網(wǎng)頁爬蟲時(shí)忽略已經(jīng)判定的URL路徑
• 郵箱通過設(shè)置過濾垃圾郵件
• 集合重復(fù)元素的判別，有效判斷元素不在集合中
• 防止數(shù)據(jù)緩存時(shí)的緩存穿透問題

優(yōu)缺點(diǎn)

• 優(yōu)點(diǎn)
  • 相比于其它的數(shù)據(jù)結(jié)構(gòu)，布隆過濾器在空間和時(shí)間方面都有巨大的優(yōu)勢(shì)。
  • 布隆過濾器存儲(chǔ)空間和插入/查詢時(shí)間都是常數(shù)。
  • Hash函數(shù)相互之間沒有關(guān)系，方便由硬件并行實(shí)現(xiàn)。
  • 布隆過濾器不需要存儲(chǔ)元素本身，對(duì)保密要求非常嚴(yán)格的場(chǎng)合有優(yōu)勢(shì)。
  • 布隆過濾器可以表示全集，其它任何數(shù)據(jù)結(jié)構(gòu)都不能。
• 缺點(diǎn)
  • 元素存在的誤判
  • 一般情況下不支持元素（位陣列）的刪除

實(shí)現(xiàn)原理

核心其實(shí)是元素如何存儲(chǔ)？如何判斷元素是否存在？核心方法就兩個(gè)，一個(gè)“存”一個(gè)檢查，里面涉及到了算法相關(guān)知識(shí)，感興趣可以深入研究下其實(shí)現(xiàn)原理與思想。

• put 將元素放入過濾器中，但不是存儲(chǔ)

public < T > boolean put(@ParametricNullness T object, Funnel< ? super T > funnel, int numHashFunctions, LockFreeBitArray bits) {
            long bitSize = bits.bitSize(); // 位數(shù)組，可以通過redis來實(shí)現(xiàn)分布式的布隆過濾器
            long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong(); //通過funnel將對(duì)象轉(zhuǎn)換成基本類型并計(jì)算64位hash
            int hash1 = (int)hash64; // 取低32位
            int hash2 = (int)(hash64 > >> 32); // 取高32位
            boolean bitsChanged = false;
            // 
            for(int i = 1; i <= numHashFunctions; ++i) {
                int combinedHash = hash1 + i * hash2;
                if (combinedHash < 0) {
                    combinedHash = ~combinedHash;
                }

                bitsChanged |= bits.set((long)combinedHash % bitSize);
            }

            return bitsChanged;
        }

• mightContain 與put相似，計(jì)算的過程相同，不同的是值的判斷

public < T > boolean mightContain(@ParametricNullness T object, Funnel< ? super T > funnel, int numHashFunctions, LockFreeBitArray bits) {
            long bitSize = bits.bitSize();
            long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong();
            int hash1 = (int)hash64;
            int hash2 = (int)(hash64 > >> 32);

            for(int i = 1; i <= numHashFunctions; ++i) {
                int combinedHash = hash1 + i * hash2;
                if (combinedHash < 0) {
                    combinedHash = ~combinedHash;
                }

                if (!bits.get((long)combinedHash % bitSize)) {
                    return false;
                }
            }

            return true;
        }

我們可以簡單第理解其實(shí)現(xiàn)原理？比如現(xiàn)在有一個(gè)容器，我們定義為String[] bitArray = new String[26]作為 位陣列 ， 現(xiàn)在有一堆由小寫英文組成的元素，我們假定Hash算法為a-z到1~26的映射。

1. 現(xiàn)在有一個(gè)元素abc，hash后為1110000000...，保存到bitArray ：1110000000...
2. 現(xiàn)在有一個(gè)元素cde, hash后為0011100000...，保存到bitArray ：1111100000...
3. 現(xiàn)在又有一個(gè)新的元素ade，hash后同樣為100110000...，很明顯會(huì)認(rèn)為該元素存在，這就是FFP

為什么判斷元素一定不在集合中呢？很顯然，如果一個(gè)元素存在，則該元素hash后的bit數(shù)組必須全部都是1，反之則不存在

示例

@Test
    public void match(){
        BloomFilter filter = BloomFilter.create(Funnels.stringFunnel(Charset.defaultCharset()),10000,0.2);
        List< String > ids = new ArrayList<  >();

        IntStream.rangeClosed(1,10000).forEach(index- >{
            String id = UUID.randomUUID().toString();
            ids.add(id);
            filter.put( id );
        });

        ids.forEach(id- >{
            // 正常情況下全部失敗，但是會(huì)有 20%的返回true
            System.out.println( id + ":" + filter.mightContain( id+1 ));
        });
    }

流程很簡單：

1. 根據(jù)配置構(gòu)建BloomFilter對(duì)象
2. 通過put方法，初始化數(shù)據(jù)到filter
3. 通過方法mightContain判斷元素是否存在

結(jié)束語

BloomFilter雖然看起來簡單，但是其內(nèi)部的實(shí)現(xiàn)包含了很多的數(shù)學(xué)與算法知識(shí)，我們只是通過其簡單的API就能各種復(fù)雜的功能。關(guān)于如何將目前說到的這些在具體的項(xiàng)目中進(jìn)行實(shí)踐與集成 后面會(huì)來介紹，首先我們能夠先了解一些技術(shù)一起能解決上面問題，理解了原理與目的，使用也就不是難事。