引言
加法器是非常重要的,它不僅是其它復雜算術運算的基礎,也是 CPU 中 ALU 的核心部件(全加器)。兩個二進制數之間的算術邏輯運算例如加減乘除,在數字計算機中都是化為若干步加法操作進行的,因此,學好數字電路,從學好加法器開始。
加法器分為半加器和全加器。全加器和半加器相比也就多了那么一個相加的進位輸入,全加器就是三位相加,半加器就是二位相加。例如,我們在做加法運算的時候,總是需要進行低位進位的判斷,從而再進行下一位的計算,這就是全加器的由來。詳細的也可以參考百度百科。
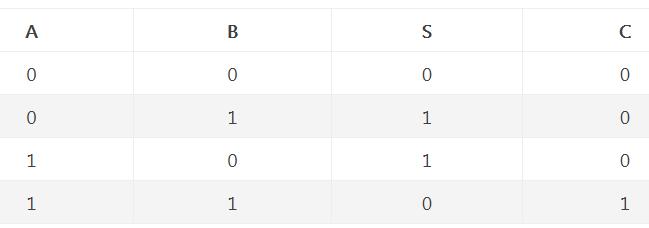
一、半加器的 Verilog 代碼實現和 RTL 電路實現
module Half_Adder(
input wire a, // 加數
input wire b, // 加數
output reg sum, // 和
output reg cout // 進位輸出
);
// 行為描述
always @(a or b) begin
sum = a ^ b; // 實踐證明,這里 <= 和 = 的結果都一樣;都是純粹的組合邏輯;
cout = a & b;
end
// 數據流描述
// assign sum = a ^ b;
// assign cout = a & b;
// 門級描述
// and(cout,a,b);
// xor(sum,a,b);
endmodule
基于多種方式描述的一個全加器電路的 RTL 電路圖如下所示:
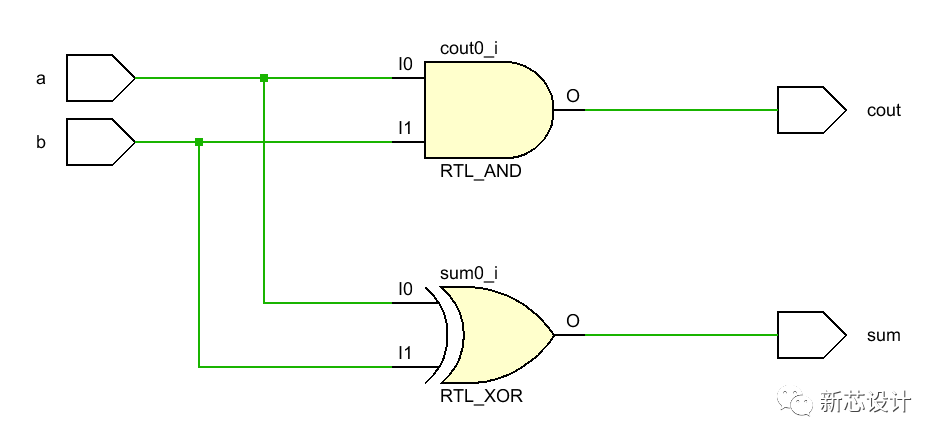
半加器的 RTL 電路實現
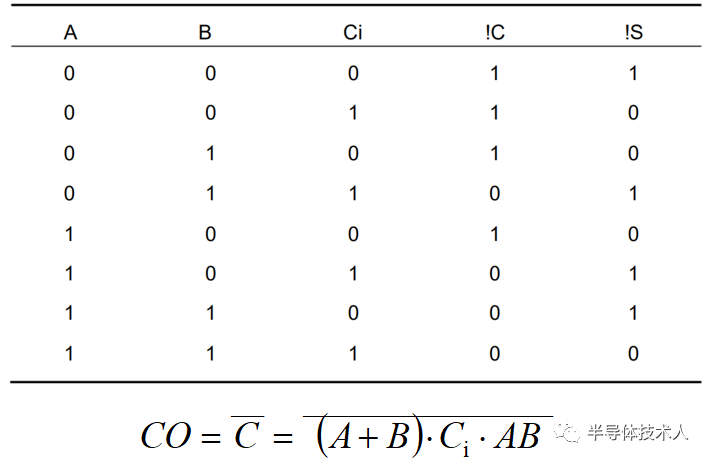
二、全加器的 Verilog 代碼實現和 RTL 電路實現
module Full_Adder(
input wire a, // 加數
input wire b, // 加數
input wire cin,// 進位輸入
output reg sum, // 和
output reg cout // 進位輸出
);
// 行為描述
always @(a or b or cin) begin
{cout,sum} <= a + b + cin;
end
// 行為描述
// always @(a or b or cin) begin
// sum = a ^ b ^ cin; // 實踐證明,這里 <= 和 = 的結果都一樣;都是純粹的組合邏輯;
// cout = a & b | b & cin | a & cin;
// end
// 數據流描述
// assign {cout,sum} = a + b + cin;
endmodule
這里,“{}” 符號表示的是 “拼接位”,即先計算 a 與 b 的值,當 a 與 b 為 “0” 和 “1” 時,它們之和為 1,那么就是{01},對應 cout 和 sum ;當 a 與 b 為 “1” 和 “1” 時,它們之和為 2,那么就是轉換為二進制就是{10},同樣對應 cout 和 sum 等等。
基于多種方式描述的一個全加器電路的 RTL 電路圖如下所示:

全加器的 RTL 電路實現
-
加法器
+關注
關注
6文章
183瀏覽量
30478 -
RTL
+關注
關注
1文章
387瀏覽量
60410 -
半加器
+關注
關注
1文章
29瀏覽量
8878 -
Verilog設計
+關注
關注
0文章
20瀏覽量
6596 -
全加器電路
+關注
關注
0文章
3瀏覽量
1660
發布評論請先 登錄
相關推薦







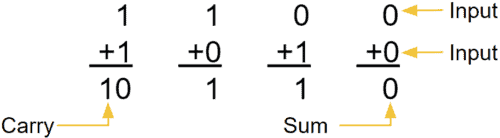












評論