1.概述:
在 PCS SVG APF UPS 等電力電子設備,都有設計合適的濾波器抑制開關諧波,濾波器在特定的工況下會產生諧振尖峰。
比如并網逆變器的LCL濾波器受電網阻抗影響,PCS離網運行受負載阻抗影響,充電樁多模塊并聯等由電抗或阻抗變化 造成諧振頻率變化,就容易產生諧振問題了。
2.LC濾波器諧振原理:
LC濾波器一般應用是典型的二階電路,串聯諧振時電路呈阻性,阻抗最小,電流達到最大也被稱為電流諧振,輸出是電容上的電壓。
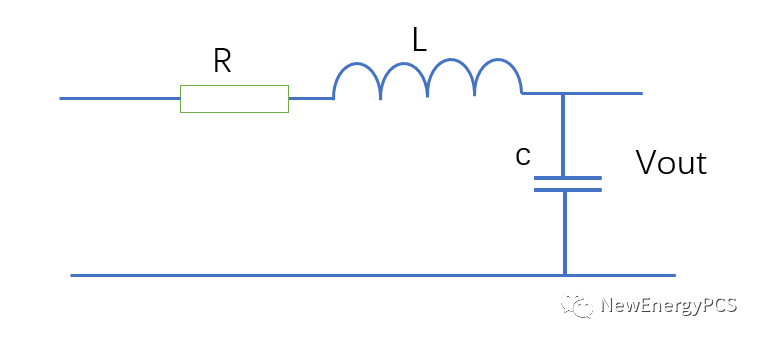
根據KVL建立動態方程:
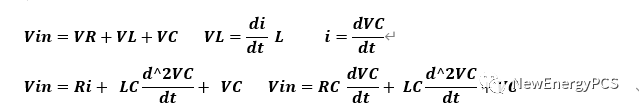 動態方程得到了二階非齊次方程,如果要解決諧振問題,那么需要找到二階非齊次方程的通解和特解。二階非齊次方程比較難求解,把它變成二階線性微分方程的標準形式和特征方程。
動態方程得到了二階非齊次方程,如果要解決諧振問題,那么需要找到二階非齊次方程的通解和特解。二階非齊次方程比較難求解,把它變成二階線性微分方程的標準形式和特征方程。
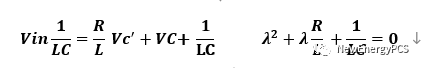
電路微分方程的特征根稱為電路的固有頻率,R L C取值不同,特征根有三種情況。兩個不相等的實數根,過阻尼狀態,兩個相等實數根,臨界阻尼狀態。共軛復數根,欠阻尼狀態。
過欠阻尼數學模型和函數圖像:


此時衰減震蕩,衰減系數和阻尼電阻的取值有關,決定了衰減的快慢。如果阻尼電阻為零,衰減系數為零,就會等幅震蕩。電感的磁場和電容的電場,相互交換。
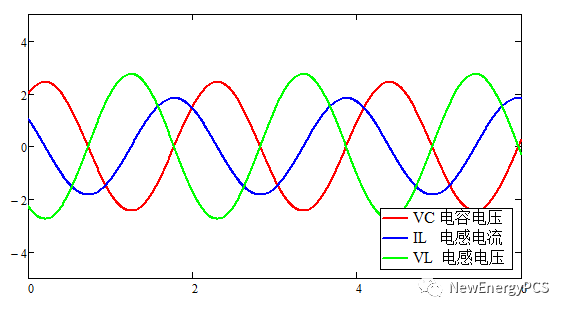
過阻尼函數圖像:
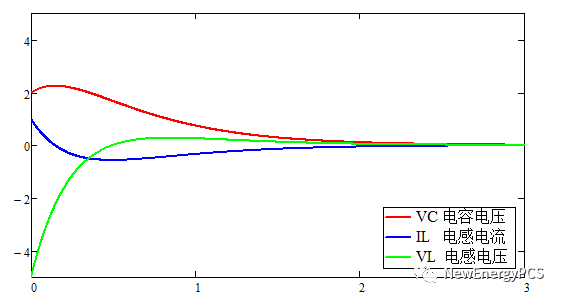
過阻尼放電,臨界阻尼類似以指數規律衰減。由于通解公式不同。模型中沒有建立。
通過建立時域模型小結:
1.調整阻尼電阻R,R值越大可以發現函數波形越不容震蕩,R值越小容易進入欠阻尼。就越容易震蕩產生尖峰。
2.調整濾波電容C,C值增大可以發現函數波形幅值變小,C值減小可以發現函數波形幅值變大。
3.調整濾波電感L,,L值減小可以發現函數波形幅值變小,L值增大可以發現函數波形幅值變大。
3.LC濾波器頻域分析:
上述用動態方程分析LC濾波器有很多不方便的地方。LC為二階濾波器,求解微分方程還行,LCL這種三階微分方程求解就比較復雜了。用傳遞函數和伯德圖來看消除諧振尖峰效果。
傳遞函數:
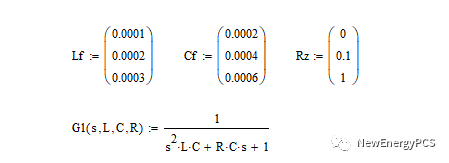
伯德圖:

伯德圖可以看出不同阻尼電阻的諧振尖峰抑制效果
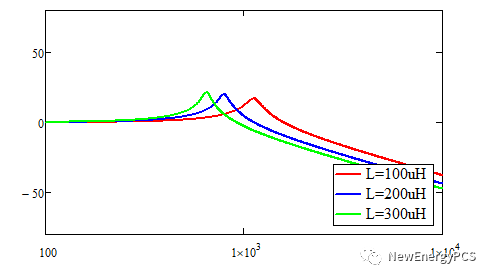
伯德圖可以看出不同濾波電感的諧振尖峰抑制效果
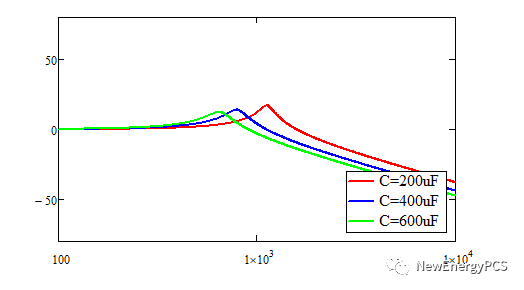
伯德圖可以看出不同濾波電容的諧振尖峰抑制效果
-
逆變器
+關注
關注
285文章
4728瀏覽量
207027 -
LC濾波器
+關注
關注
12文章
93瀏覽量
21684 -
PCS
+關注
關注
1文章
141瀏覽量
14684 -
二階電路
+關注
關注
0文章
16瀏覽量
9835 -
諧振抑制
+關注
關注
0文章
5瀏覽量
1797
發布評論請先 登錄
相關推薦
托克托電廠阻塞濾波器模態中心頻率偏移對抑制次同步諧振的影響
LC濾波器設計和制作方法的實用工具書:LC濾波器設計與制作PDF
LCL和LC濾波器的區別
如何進行大容量PWM壓源逆變器的LC濾波器設計
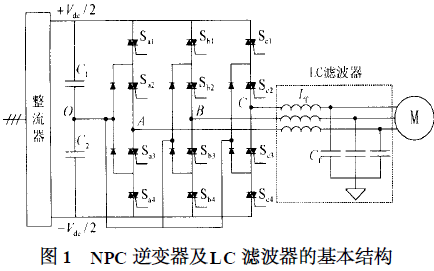




 LC濾波器諧振抑制概述
LC濾波器諧振抑制概述












評論