前 言
SAIMO
Preface
基于仿真的自動駕駛可靠性估計(一)中已經介紹,使用定步長泛化、樸素蒙特卡羅等方法生成驗證自動駕駛系統的仿真場景難以在可以接受的成本內精確估計被測試系統在指定邏輯場景即測試空間內的失效概率。本文將由此出發,介紹若干可以用來估計罕見事件發生概率的可靠性分析方法。
01. 問題定義
我們將一個擁有D個可泛化參數的邏輯場景等價于維參數空間,其中是一組隨機變量,其分布函數由邏輯場景決定,而的一組具體取值即為此邏輯場景下的一個具體場景。
被測試自動駕駛系統或車輛在某一具體場景中失效,指該系統及車輛的某項評價指標(kpi)處于失效域中。我們用表示某項kpi在場景上的取值,不失一般性地用表示此項kpi處于失效域中。故被測試系統或車輛在某一邏輯場景中的失效概率等價于對應測試空間中,參數組合落入失效域的概率,即
其中為此邏輯場景中參數的聯合分布。
本文剩余部分將介紹若干精確高效估計此概率的可靠性分析方法并通過數值實現說明其效率。一般我們會在標準正態空間中使用這些可靠性分析方法,故我們提前使用Rosenblatt變換將測試空間轉化為標準正態分布空間,之后的討論均基于標準正態分布空間。
02.一階可靠性分析方法(FORM)
一種經典的可靠性分析算法是將在失效臨界面(即的區域)上的一個點利用泰勒展開進行線性近似,即再通過來估計。如下圖所示,右上角的區域為失效域,FORM用線性展開即黃色線以上的區域來代替實際失效區域。
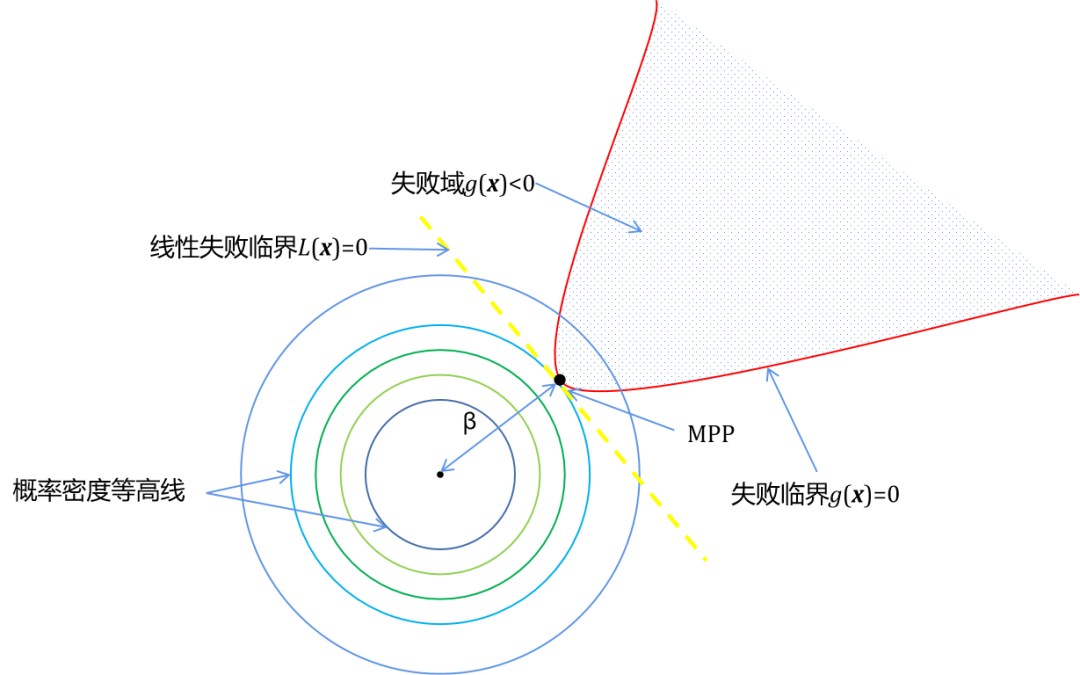
顯然失效臨界的形狀及的選取對近似的結果有很大的影響,直觀想來我們會選取失效臨界中最可能的點(實際是似然函數最大的點)MPP做為展開的中心,即 此時利用正態分布的性質及的約束可以證明其中為標準正態分布函數的概率分布函數,為原點到MPP的距離。可以看出FORM的精度取決于失效臨界與線性邊界的差距,而FORM算法的效率只取決于尋找MPP算法的速度。最早使用Rackwith-Fiessler算法來快速尋找MPP點,然而此算法并不能保證收斂,故在Rackwith-Fiessler算法不收斂時可以使用更為復雜的優化算法來實現,例如NLPQL。
03. 方向采樣算法
將測試空間考慮成一個多維球體,若在每個方向上存在最多一個失效臨界時,可以通過方向采樣算法估計失效概率。其基本原理是
1. 在半徑為的層球面進行均勻采樣,并記錄其中的失效場景;
2. 對失效場景所在的方向插值求解此方向的失效臨界場景;
3.注意測試空間為維標準正態分布空間,故其中任意一點與原點距離的平方服從自由度為的卡方分布(),故可對失效概率估計如下
其中是總采樣數,是失效方向數,是第個失效方向的臨界場景與原點間的距離。
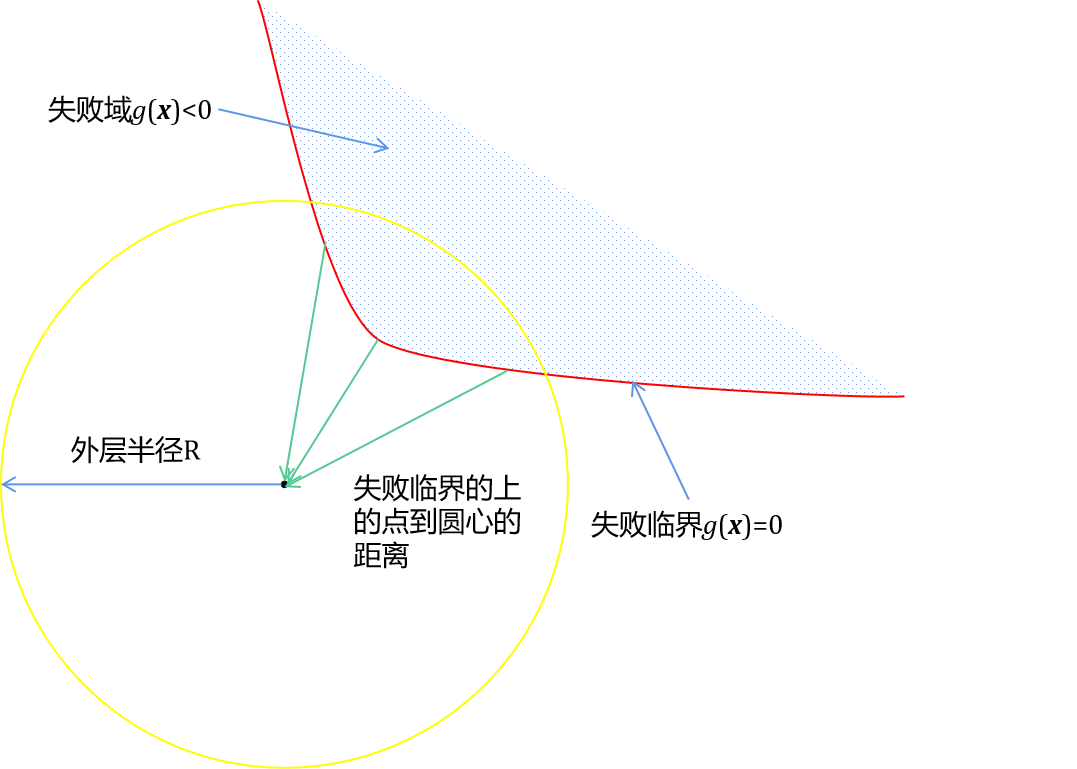
通過上面的介紹可以看出,方向采樣算法無法觀察到距離原點超過R的失效場景。在標準正態分布空間中無法觀測的失效場景概率占比小于等于,故往往取比較大的值例如至,如此漏掉的失效場景占比僅在至,是完全可以接受的。影響此算法精度的另一個因素是在外層球面采樣的均勻程度,我們使用球面拉丁超立方采樣代替傳統的方法獲取高維球面上的超均勻樣本,用相同數量的樣本實現對球面更好的覆蓋。
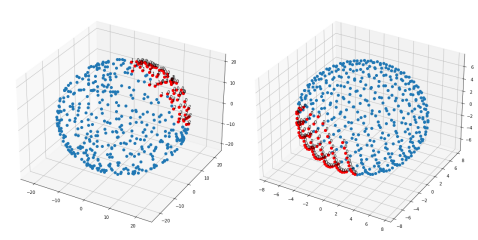
04. 重要性采樣算法
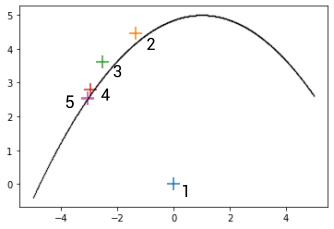
重要性采樣算法直接從蒙特卡羅方法失效的原因出發,使用提議分布來代替真實分布以期采集到更多的失效場景,并根據下面的方法估計失效概率其中是根據提議分布的采樣數,是其中的第個樣本觀察值。可以簡單的看出重要性采樣算法是失效概率的無偏估計,但算法的精度(相對誤差)主要取決于提議分布的選取,在最優提議分布,,下的相對誤差是0!但是這樣的提議分布顯然是無法獲取的,因為分母本身就是我們要估計的量,所以實際應用中會采用各種方法來逼近。我們選取混合高斯分布作為提議分布,使用交叉熵優化的方法基于每輪采樣的結果自適應調整提議分布中的參數,實現對全部主導失效域的覆蓋及失效概率的估計。下面的圖說明了使用重要性采樣的方法,自適應調整提議分布尋找失效樣本和失效臨界場景的過程。

重要性采樣算法。其中藍色點為安全場景,黃色點為本輪采樣中較危險場景,紅色點為失效場景,紫色點為失效臨界場景。其中左上和右小角的是小邊界為線性,左下和右上角的失效邊界為非線性。
05. 數值實驗
下面將用2個數值實驗,證明不同可靠性分析算法的有效性。
數值實驗一:
| 可靠性分析方法 | FORM |
| 測試空間 | |
| kpi函數 | |
| 理論失敗概率 |
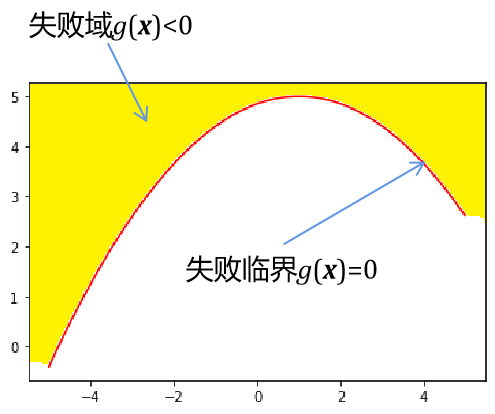
由于kpi函數的連續性及凸凹性較好,使用Rackwith-Fiessler算法快速迭代尋找MPP,得到如下實驗結果
| 失敗概率估計 | |
| 相對偏差 | 16% |
| 相對誤差 | 0,FORM方法不使用隨機采樣 |
| kpi函數調用次數 | 5次,5次迭代尋找MPP |
可以看當線性展開可以比較好的逼近失效臨界是,FORM方法可以很好的估計失效概率。此例中雖然無法在全局使用線性展開逼近失效臨界,但在MPP點附近逼近效果較好,即在對失效概率貢獻最大的區域逼近效果較好,故可以得到較好的估計效果。
數值實驗二
實驗二中我們使用測試空間中的Katsuki函數作為kpi函數,即 Katsuki函數通過是具備了不同形狀的失效臨界,其理論失效概率為。使用方向采樣及重要性采樣對其進行估計,下面將展示兩種算法的結果

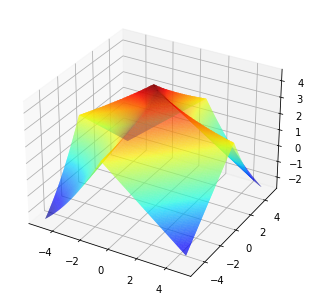
此實驗中方向采樣算法的球面采樣數為100,臨界面尋找的最大迭代次數為10;重要性采樣每輪采樣數為500。因為測試空間維度較低,方向采樣有著非常優秀的表現,同時兩者對比蒙特卡羅方法都體現出了超高的效率。需要注意的是,雖然重要性采樣使用的kpi函數平均次數更多,但在并行仿真下實際只有4輪仿真;而kpi調用次數較少的方向采樣因為缺乏并行仿真支撐能力,耗時反而更長。
最后對不同的可靠性分析算法能夠適應的情景做出分析,需要注意的是蒙特卡羅方法或拉丁超立方/sobol方法雖然不受測試空間的限制,但其效率僅能應對概率在及更大的情況。
掃描二維碼
關注賽目科技
 ?
?專注智能網聯汽車
測試丨驗證丨評價研究
作者:算法研究部-姚尚辰
原文標題:基于仿真的自動駕駛可靠性估計(二)
文章出處:【微信公眾號:賽目科技】歡迎添加關注!文章轉載請注明出處。
-
賽目科技
+關注
關注
0文章
41瀏覽量
715
原文標題:基于仿真的自動駕駛可靠性估計(二)
文章出處:【微信號:gh_c85a8e3c0f2a,微信公眾號:賽目科技】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
激光雷達光電組件的AEC-Q102認證:保障自動駕駛硬件的可靠性與品質

AUTOSAR通信對自動駕駛的影響 AUTOSAR通信與嵌入式系統設計
基于場景的自動駕駛驗證策略


FPGA在自動駕駛領域有哪些優勢?
FPGA在自動駕駛領域有哪些應用?
中級自動駕駛架構師應該學習哪些知識
初級自動駕駛架構師應該學習哪些知識
長電科技為自動駕駛芯片客戶提供多樣化高可靠性的封裝測試解決方案




 基于仿真的自動駕駛可靠性估計(二)
基于仿真的自動駕駛可靠性估計(二)












評論