SymPy 是一個Python庫,專注于符號數學,它的目標是成為一個全功能的計算機代數系統,同時保持代碼簡潔、易于理解和擴展。
舉一個簡單的例子,比如說展開二次方程:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = ((x+y)**2).expand()
print(d)
# 結果:x**2 + 2*x*y + y**2
你可以隨便輸入表達式,即便是十次方,它都能輕易的展開,非常方便:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = ((x+y)**10).expand()
print(d)
# 結果:x**10 + 10*x**9*y + 45*x**8*y**2 + 120*x**7*y**3 + 210*x**6*y**4 + 252*x**5*y**5 + 210*x**4*y**6 + 120*x**3*y**7 + 45*x**2*y**8 + 10*x*y**9 + y**10
下面就來講講這個模塊的具體使用方法和例子。
1.準備
開始之前,你要確保Python和pip已經成功安裝在電腦上,如果沒有,可以訪問這篇文章:超詳細Python安裝指南 進行安裝。
**(可選1) **如果你用Python的目的是數據分析,可以直接安裝Anaconda:Python數據分析與挖掘好幫手—Anaconda,它內置了Python和pip.
**(可選2) **此外,推薦大家用VSCode編輯器,它有許多的優點:Python 編程的最好搭檔—VSCode 詳細指南。
請選擇以下任一種方式輸入命令安裝依賴 :
- Windows 環境 打開 Cmd (開始-運行-CMD)。
- MacOS 環境 打開 Terminal (command+空格輸入Terminal)。
- 如果你用的是 VSCode編輯器 或 Pycharm,可以直接使用界面下方的Terminal.
pip install Sympy
2.基本使用
簡化表達式(化簡)
sympy支持三種化簡方式,分別是普通化簡、三角化簡、指數化簡。
普通化簡 simplify( ):
from sympy import *
x = Symbol('x')
d = simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))
print(d)
# 結果:x - 1
三角化簡 trigsimp( ):
from sympy import *
x = Symbol('x')
d = trigsimp(sin(x)/cos(x))
print(d)
# 結果:tan(x)
指數化簡 powsimp( ):
from sympy import *
x = Symbol('x')
a = Symbol('a')
b = Symbol('b')
d = powsimp(x**a*x**b)
print(d)
# 結果:x**(a + b)
解方程 solve()
第一個參數為要解的方程,要求右端等于0,第二個參數為要解的未知數。
如一元一次方程:
from sympy import *
x = Symbol('x')
d = solve(x * 3 - 6, x)
print(d)
# 結果:[2]
二元一次方程:
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = solve([2 * x - y - 3, 3 * x + y - 7],[x, y])
print(d)
# 結果:{x: 2, y: 1}
求極限 limit()
dir=’+’表示求解右極限,dir=’-‘表示求解左極限:
from sympy import *
x = Symbol('x')
d = limit(1/x,x,oo,dir='+')
print(d)
# 結果:0
d = limit(1/x,x,oo,dir='-')
print(d)
# 結果:0
求積分 integrate( )
先試試求解不定積分:
from sympy import *
x = Symbol('x')
d = integrate(sin(x),x)
print(d)
# 結果:-cos(x)
再試試定積分:
from sympy import *
x = Symbol('x')
d = integrate(sin(x),(x,0,pi/2))
print(d)
# 結果:1
求導 diff()
使用 diff 函數可以對方程進行求導:
from sympy import *
x = Symbol('x')
d = diff(x**3,x)
print(d)
# 結果:3*x**2
d = diff(x**3,x,2)
print(d)
# 結果:6*x
解微分方程 dsolve( )
以 y′=2xy 為例:
from sympy import *
x = Symbol('x')
f = Function('f')
d = dsolve(diff(f(x),x) - 2*f(x)*x,f(x))
print(d)
# 結果:Eq(f(x), C1*exp(x**2))
3.實戰一下
今天群里有同學問了這個問題,“大佬們,我想問問,如果這個積分用Python應該怎么寫呢,謝謝大家”:
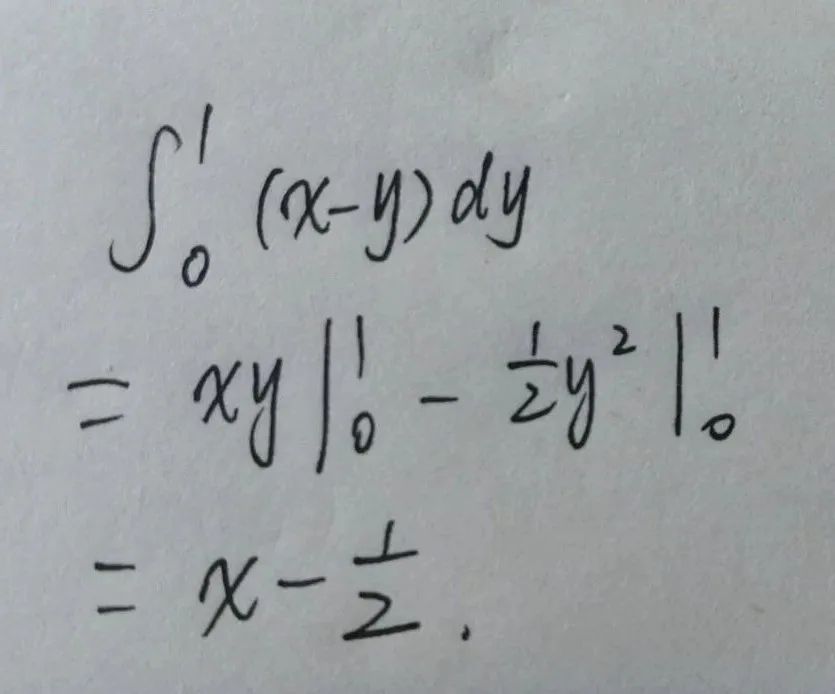
# Python 實用寶典
from sympy import *
x = Symbol('x')
y = Symbol('y')
d = integrate(x-y, (y, 0, 1))
print(d)
# 結果:x - 1/2
為了計算這個結果,integrate的第一個參數是公式,第二個參數是積分變量及積分范圍下標和上標。
運行后得到的結果便是 x - 1/2 與預期一致。
如果大家也有求解微積分、復雜方程的需要,可以試試sympy,它幾乎是完美的存在。
-
模塊
+關注
關注
7文章
2722瀏覽量
47583 -
計算機
+關注
關注
19文章
7520瀏覽量
88262
發布評論請先 登錄
相關推薦
matlab數學建模工具箱
如何用Labview解復雜的數學方程?
分享《Matlab與微積分》課件
RC微積分電路的Multisim仿真
MATLAB教程之如何使用MATLAB求解數學問題資料概述
深度解讀你也能懂的微積分
硬件設計為何還要學習微積分?
Banach空間幾類分數階微積分方程的mild解的存在性

戴維·M. 布雷蘇:對微積分的思考
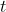
SymPy:四行代碼秒解微積分
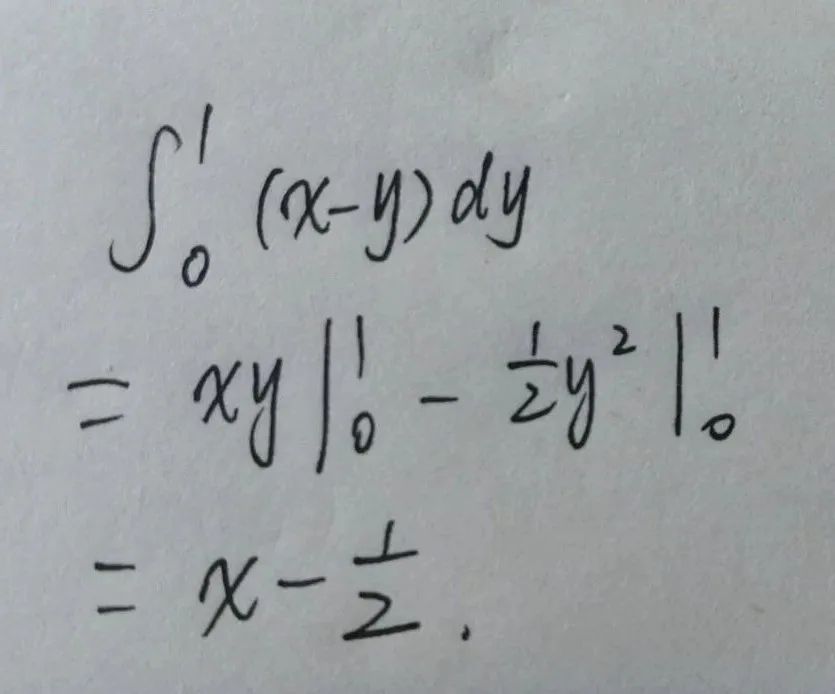




 Sympy模塊如何解數學方程解微積分
Sympy模塊如何解數學方程解微積分











評論