1.1 什么是圖(graph)?
在圖論的上下文中,圖是一種結構化數據類型,具有節點(nodes)(保存信息的實體)和邊緣(edges)(連接節點的連接,也可以保存信息)。
圖是一種數據結構的方式,但它本身可以是一個數據點。圖是一種非歐幾里得數據類型,這意味著它們存在于三維空間,不像其他數據類型,比如圖像、文本和音頻。
圖可以具有某些屬性,這些屬性限制了可以對其執行的可能操作和分析。這些屬性可以被定義。
1.2 圖的定義
首先,讓我們介紹一些定義。
在計算機科學中,我們經常談論一種稱為圖的數據結構:
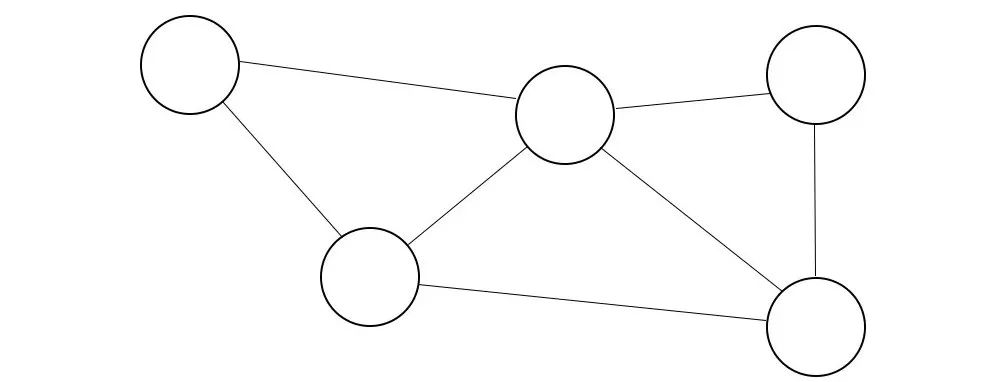
圖的邊緣和/或節點上可以有標簽,讓我們給它一些邊緣和節點的標簽。

標簽也可以被視為權重,但這取決于圖的設計者。
標簽不必是數字,它們可以是文本的。

標簽不必是唯一的;給多個節點相同的標簽是完全可能的,有時也是有用的。例如,氫分子就是一個例子:

注意混合了數值和文本數據類型
圖可以具有特征(也稱為屬性)。

要小心不要混淆特征和標簽。一個簡單的思考方式是使用名稱、角色和人的類比:
一個節點就是一個人,一個節點的標簽就是一個人的名字,而節點的特征就是這個人的特點。
圖可以是有向的或無向的:

請注意,有向圖也可以具有無向邊
圖中的一個節點甚至可以有指向自身的邊緣。這被稱為自環(self-loop)。
圖可以是:
- 異構的(Heterogeneous) — 由不同類型的節點組成
- 同構的(Homogeneous) — 由相同類型的節點組成
并且可以是:
- 靜態的(Static) — 節點和邊不變,沒有添加或刪除
- 動態的(Dynamic) — 節點和邊發生變化,添加、刪除、移動等
粗略地說,圖可以模糊地描述為:
- 密集的(Dense) — 由許多節點和邊組成
- 稀疏的(Sparse) — 由較少的節點和邊組成
通過將它們轉化為平面形式,可以使圖看起來更整潔,這基本上意味著重新排列節點,使邊不相交。

當我們探索目前在各種GNN架構中使用的許多不同方法時,這些概念和術語將會派上用場。其中一些基本方法在以下方面進行了描述:
1.3 圖分析
有各種不同的圖結構可供ML模型學習(Wheel,Cycle,Star,Grid,Lollipop,Dense,Sparse等)。
你可以遍歷一個圖:

Jon在4個時間步驟內從Bob到Bic;他最好希望不下雪!
在這種情況下,我們正在遍歷一個無向圖。顯然,如果圖是有向的,那么只需按照邊的方向前進。有幾種不同類型的遍歷,所以要注意措辭。以下是一些最常見的圖遍歷術語及其含義:
- 行走(Walk):圖的遍歷 —— 閉合行走是指目標節點與源節點相同
- 小徑(Trail):沒有重復邊的行走 —— 電路(Circuit)是閉合小徑
- 路徑(Path):沒有重復節點的行走 —— 循環(Cycle)是閉合路徑
在遍歷的概念基礎上,人們還可以在圖上發送消息。

Sam?更像是S-p-am(垃圾郵件)...
所有的Sam的鄰居都給他發送了一條消息,其中t代表時間步驟。Sam可以選擇打開他的郵箱并更新自己的信息。在具有注意機制的模型中,信息在網絡中傳播的概念非常重要。在圖中,消息傳遞是我們泛化卷積的一種方式。稍后會詳細討論。
1.4 E-圖 — 計算機上的圖
通過學習所有這些,你現在對圖理論有了基本的理解!任何對GNNs重要的其他概念將會隨著它們的出現而進行解釋,但與此同時,還有一個關于圖的最后一個主題我們需要涵蓋。我們必須學會如何在計算中表達圖。
有幾種方法可以將圖轉化為計算機可以處理的格式;它們都是不同類型的矩陣。
關聯矩陣Incidence Matrix(I):
關聯矩陣通常在研究論文中用大寫字母I表示,由1、0和-1組成,關聯矩陣可以按照以下簡單的模式制作:

從圖到關聯矩陣
(帶權重的)鄰接矩陣Adjacency Matrix(A):
圖的鄰接矩陣由1和0組成,除非它是加權或帶標簽的。在任何情況下,A都可以按照以下規則構建:

無向圖的鄰接矩陣因此在其對角線上是對稱的,從左上角對象到右下角:

有向圖的鄰接矩陣只覆蓋對角線線的一側,因為有向圖的邊只朝一個方向。
鄰接矩陣可以是“帶權重的”,這基本上意味著每條邊都有與之關聯的值,所以不是1,而是將值放在相應的矩陣坐標中。這些權重可以代表任何你想要的東西。例如,在分子的情況下,它們可以表示兩個節點(原子)之間的鍵的類型。在LinkedIn這樣的社交網絡中,它們可以表示兩個節點(人)之間的1st、2nd或3rd級連接。
邊的權重概念是使GNNs如此強大的一個屬性;它們允許我們考慮結構性(依賴性)和獨立性信息。對于實際應用,這意味著我們可以考慮外部和內部信息。
度矩陣(D):
圖的度矩陣可以通過之前介紹的度概念來找到。D本質上是一個對角矩陣,其中對角線的每個值都是其對應節點的度數。

各種類型的圖和矩陣(由歐洲生物信息學研究所提供)
不要忘記度數只是鄰接矩陣的每一行的總和。然后,這些度數被放在矩陣的對角線上(鄰接矩陣的對稱線)。這很好地引出了最后的矩陣:
拉普拉斯矩陣(L):
圖的拉普拉斯矩陣是通過從鄰接矩陣中減去度矩陣而得到的:

度矩陣中的每個值都減去了相應的鄰接矩陣中的值,如下所示:
 圖矩陣三合一(由維基百科提供)
圖矩陣三合一(由維基百科提供)
還有其他圖矩陣表示法,如關聯矩陣,但絕大多數應用于圖類型數據的GNN應用都使用這三個矩陣中的一個、兩個或全部。這是因為它們,尤其是拉普拉斯矩陣,提供了關于實體(具有屬性的元素)和關系(實體之間的連接)的重要信息。
唯一缺失的是一個規則(將實體通過關系映射到其他實體的函數)。這就是神經網絡派上用場的地方。
2. 深度學習
神經網絡模型(或簡稱NN)及其擴展家族,包括卷積神經網絡、循環神經網絡,當然還有圖神經網絡,都是深度學習算法的一種類型。
一切都始于謙卑的線性方程。
如果我們將這個方程結構化為一個感知器,我們可以看到:

其中輸出( )是偏差( )與輸入( )乘以權重( )的和( )。
神經網絡通常具有激活函數,它基本上決定了一個給定神經元的輸出( )是否應該被認為是“激活的”,并將感知器的輸出值保持在一個合理的可計算范圍內(例如,sigmoid函數用于 范圍,tanh函數用于 范圍,ReLU函數用于 或 等)。這就是為什么我們在感知器的末端附加激活函數的原因。

當我們將一堆感知器放在一起時,我們得到了一個類似于神經網絡開端的東西!這些感知器將數值值從一層傳遞到另一層,每一次傳遞都將該數值值接近網絡經過訓練的目標/標簽。

當你把一堆感知器放在一起時,你會得到:

一個普通的NN(由Digital Trends提供)
要訓練神經網絡,我們首先需要計算我們需要調整模型權重的量。我們使用損失函數來做到這一點,它計算誤差。
其中 是誤差, 是期望的輸出, 是實際輸出。在高層次上,誤差計算為實際輸出(神經網絡的預測)減去期望輸出(目標)。目標是最小化誤差。通過使用稱為反向傳播的過程來調整每一層的權重來最小化誤差。
基本上,反向傳播將調整從輸出層傳播到輸入層的整個網絡。所調整的量由接收誤差作為輸入的優化函數確定。優化函數可以被想象成一個球在山上滾動,球的位置就是誤差。因此,當球滾到山底時,誤差達到最小值。
此外,還有一些必須定義的超參數,其中最重要的之一是學習率。學習率調整了優化函數應用的速率。學習率就像重力設置;重力越大(學習率越高),球滾得越快,反之亦然。
神經網絡具有許多不同的宏觀和微觀自定義選項,使每個模型都具有獨特的特點,性能各異,但它們都是基于這個基本模型的。稍后我們將看到,這對于圖學習尤其如此。根據需要將介紹卷積和重復等操作。
3. 深度神經網絡就是一種圖
文章到此,你可能已經注意到一個微妙但顯而易見的事實:
神經網絡實際上就是圖!
神經網絡是一種特殊的圖,但它們具有相同的結構,因此具有相同的術語、概念和規則。
回想一下感知器的結構本質。我們可以將輸入值( )、偏差值( )和求和運算( )視為圖中的3個節點。我們可以將權重( )視為連接輸入值( )和求和運算( )的邊。
神經網絡最相似的具體類型是多部分圖。多部分圖是可以分成不同節點集的圖。每個節點集中的節點可以在節點集之間共享邊,但不能在每個節點集內部共享邊。

同構二分圖(由Wolfram MathWorld提供)
有些神經網絡甚至具有完全連接的節點、條件節點和其他瘋狂的架構,這些架構賦予了神經網絡其特有的多功能性和強大性能;以下是一些最流行的架構:

神經網絡動物園(由Asimov Institute提供)
每種顏色對應于不同類型的節點,可以以多種不同的方式排列。通過網絡中的數據前向或后向傳播類似于圖中的消息傳遞。圖中的邊緣或節點特征類似于神經網絡中的權重。請注意,一些節點甚至具有我們之前提到的自環(RNNs — 循環神經網絡中的特性)。
神經網絡并不是唯一具有類似圖結構的機器學習模型。
- K均值
- K最近鄰
- 決策樹
- 隨機森林
- 馬爾可夫鏈
如上模型,它們本身都具有圖形結構,或者以圖形結構輸出數據。
4. 本質上
我們涵蓋了很多內容,但回顧一下,我們深入探討了3個概念:
- 圖論
- 深度學習
- 使用圖理論的機器學習
有了這些先決條件,人們可以充分理解和欣賞圖學習。在高層次上,圖學習進一步探索并利用了深度學習和圖理論之間的關系,使用一系列設計用于處理非歐幾里德數據的神經網絡。
5. 關鍵要點
有許多關鍵要點,但要點是:
- 所有圖都具有定義其可用或可分析操作的屬性。
- 圖是使用各種矩陣來進行計算表示的。每個矩陣提供不同數量或類型的信息。
- 深度學習是機器學習的一個子集,大致模擬人類大腦中神經元工作的方式。
- 深度學習通過在網絡中前向傳遞信息并向后傳播神經元調整來進行迭代學習。
- 神經網絡(以及其他機器學習算法)與圖理論有密切聯系;
現在你具備了深入了解圖學習的所有先決條件。一個好的起點是研究迄今為止已經開發的各種圖神經網絡的種類。
-
音頻
+關注
關注
29文章
2891瀏覽量
81720 -
數據
+關注
關注
8文章
7104瀏覽量
89298 -
卷積
+關注
關注
0文章
95瀏覽量
18529 -
深度學習
+關注
關注
73文章
5510瀏覽量
121347
發布評論請先 登錄
相關推薦
AI、5G和生物識別上榜 阿里巴巴達摩院發布2019十大科技趨勢
Nanopi深度學習之路(1)深度學習框架分析
深度學習在汽車中的應用
如何在交通領域構建基于圖的深度學習架構
什么是深度學習?使用FPGA進行深度學習的好處?
深度學習是什么?了解深度學習難嗎?讓你快速了解深度學習的視頻講解
關系歸納偏差和深度學習及圖神經網絡的詳細資料說明

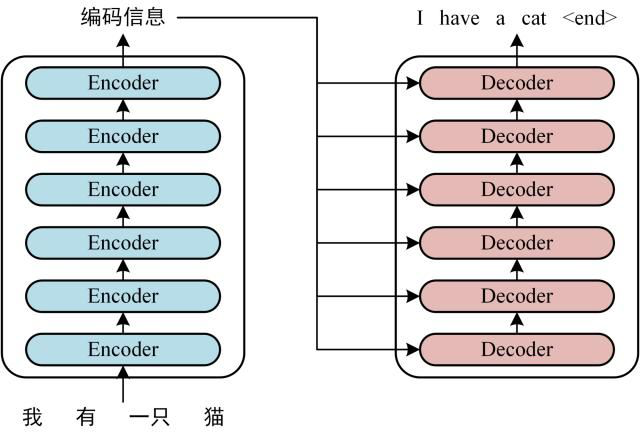
深度學習與圖神經網絡學習分享:Transformer




 深度學習的圖原理
深度學習的圖原理










評論