在控制指令下達之后,震蕩現象往往是個令人頭疼的問題,超調可能會帶來物理系統損害,從振動形式達到穩態時間需要很長時間等問題。
在有些應用之中,比如說在微機電里面,甚至會達到100%(因為其阻尼主要來自空氣阻力,而其體積又非常小,在真空中其品質因數可輕松達到1000以上,對應的阻尼系數ζ在0.001這個數量級)。如下圖所示的一個微機電執行器的階躍響應:

從控制的角度來講,這是我們不希望看到的。該怎么減小震蕩的問題?
系統零點與震蕩里面提到過反饋系統里面抵消震蕩的原理,我這次想聊一下前饋法,英文里面一般叫feedforward compensator,也有叫input shaper的,也有搞信號的就叫它是一個filter,anyway。前饋法的優點是什么?便宜,不用買傳感器;不會帶來穩定性問題。
如果對于一個線性度很好的穩定的震蕩系統,前饋法抵消應該是個很容易的事情:引入一對前饋的零點(notch filter),把震蕩的極點對給抵消了不就好了么。
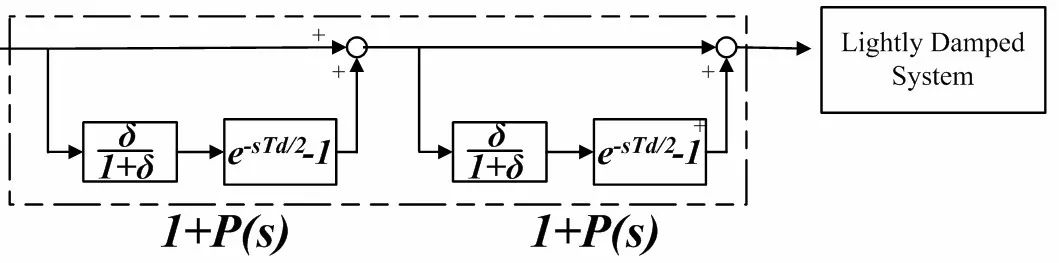
問題是,這個零點對怎么實現?純微分都不好實現,那一對共軛的零點麻煩就會更大。其實有個經典的前饋控制器叫做posicast controller:

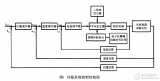
它的控制框圖也很簡單:
其中的 δ 和 Td 是非常直觀的,對于工程師們是非常容易理解和實現的,如下圖的例子,前者是超調量,后者是超調時間:

在根軌跡上來看一下發生了什么:

公式(1)其實是有個無窮零點的系統,而它的第一對零點就用來抵消掉那個不希望有的震蕩極點對。它比notch好的地方在于, 它的高頻增益是很低的,而不像notch那樣過了陷波之后就會一路走高 ,看它自己的不加log scale頻域圖的一個例子:

可見它的幅值增益是不會超過1的。即對于高頻的前饋噪聲不敏感。再看一個在頻域下抵消了震蕩極點之后的圖:

看紅線明顯可得知震蕩極點對被抵消了。
這個方法對于線性度好的穩定系統相當有效,但是如果這個極點對和零點對不匹配呢?答案是魯棒性比較差,即使有著比較小的不匹配,效果也會大打折扣:

前饋法是否就山窮水盡了?并不是。
-
傳感器
+關注
關注
2552文章
51240瀏覽量
754822 -
控制器
+關注
關注
112文章
16402瀏覽量
178608 -
前饋控制器
+關注
關注
0文章
5瀏覽量
5883
發布評論請先 登錄
相關推薦
一種新型的模糊PID控制器介紹
饋通濾波器的五種形式




 介紹一種前饋形式的振蕩控制器(上)
介紹一種前饋形式的振蕩控制器(上)











評論