希望這篇文章能夠讓你無痛理解貝葉斯優(yōu)化，記得點贊！

貝葉斯優(yōu)化什么

既然是優(yōu)化，就有優(yōu)化命題的存在，比如要在某個區(qū)間內去最大化某個函數

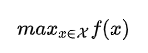
如果這個函數計算比較容易，甚至還可以知道它的梯度，那事情就好辦了，一階、二階優(yōu)化算法換著上就完事。

https://zhuanlan.zhihu.com/p/169835477

但現(xiàn)實往往沒有那么理想，這個函數的一階、二階導數信息我們可能是沒有的，甚至計算一次函數的值都很費勁（給定一個x，計算f（x） 的計算量很大。

比如神經網絡中的超參數優(yōu)化），這時候就要求助 gradient-free 的優(yōu)化算法了，這類算法也很多了，貝葉斯優(yōu)化就屬于無梯度優(yōu)化算法中的一種，它希望在盡可能少的試驗情況下去盡可能獲得優(yōu)化命題的全局最優(yōu)解。

概述

由于我們要優(yōu)化的這個函數計算量太大，一個自然的想法就是用一個簡單點的模型來近似f（x），這個替代原始函數的模型也叫做代理模型，貝葉斯優(yōu)化中的代理模型為高斯過程，假設我們對待優(yōu)化函數的先驗（prior）為高斯過程，經過一定的試驗我們有了數據（也就是evidence），然后根據貝葉斯定理就可以得到這個函數的后驗分布。

有了這個后驗分布后，我們需要考慮下一次試驗點在哪里進一步收集數據，因此就會需要構造一個acquisition函數用于指導搜索方向（選擇下一個試驗點），然后再去進行試驗，得到數據后更新代理模型的后驗分布，反復進行。

綜上所述，貝葉斯優(yōu)化的流程為：

高斯過程

高斯過程是多元高斯分布向無窮維的擴展，如果說高斯分布是隨機變量的分布，則高斯過程是函數的分布，它可以由均值函數和協(xié)方差函數組成

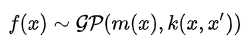
這里的均值和協(xié)方差函數的推導和具體形式先省略不管，感興趣的可以看之前的博文，需要明確的是我們已經可以根據高斯過程的后驗分布對這個未知函數在任意位置的值做出預測，均值包括方差。

關于高斯過程的更多可見：

https://zhuanlan.zhihu.com/p/158720213

acquisition函數

Typically, acquisition functions are defined such that high acquisition corresponds to potentially high values of the objective function, whether because the prediction is high, the uncertainty is great, or both.

也就是說貝葉斯優(yōu)化選擇的搜索方向為預測值大的位置或者不確定性大的位置，這樣才有可能搜到目標函數的最優(yōu)解。

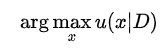
因此貝葉斯優(yōu)化中很多工作關注點在于acquisition函數的設計：

最大化提升概率

最容易想到的就是我希望下一次試驗的結果比當前所有觀測結果都要好

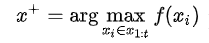
或者說這個新采樣的函數值更優(yōu)的概率要大

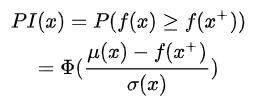
但是光這樣考慮是有點目光短淺的，它忽略了對不確定性的考慮，一味追求選擇大概率肯定大于f（x）＋的點，也就是一直在exploitation，這樣的缺點是可能就陷入了局部最優(yōu)，忽略了潛在的最優(yōu)解。改進的方法也很簡單，加個偏置就可以了

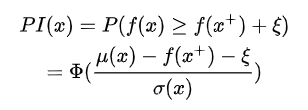
最大化提升量

提升的概率大并不意味著提升得多，一種量化的角度就是考慮提升量（可以不嚴謹地理解為梯度下降法中，不僅要下降，而且要下得更多一點）

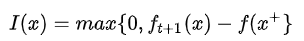
那么要求得下一次試驗點就可以最大化期望的提升量

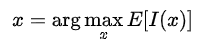
由于代替模型為高斯過程，提升量Ι的似然滿足標準正態(tài)分布，進一步可以推導（不會推導想了解推導的再留言吧）得到

最大化置信上界

由于我們的代理模型是高斯過程，預測為分布，即有均值也有方差，那么就可以構造一個置信上界

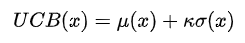
這樣的上界同時考慮了預測值的大小以及不確定性，高斯過程在觀測數據的位置不確定性（方差）小，在未探索區(qū)域的不確定大。

Talk is Cheap

讓我們來解讀一下源碼，一探究竟

首先定義個Bayesian_opt的類，其中的代理模型高斯過程從sklearn拉出來就好了

from sklearn.gaussian_process import GaussianProcessRegressor
self.GP = GaussianProcessRegressor(...)

定義acquisition function

def PI(x, gp, y_max, xi):
  mean, std = gp.predict(x, return_std=True)
  z = (mean - y_max - xi)/std
  return norm.cdf(z)
def EI(x, gp, y_max, xi):
  mean, std = gp.predict(x, return_std=True)
  a = (mean - y_max - xi)
  z = a / std
  return a * norm.cdf(z) + std * norm.pdf(z)
def UCB(x, gp, kappa):
  mean, std = gp.predict(x, return_std=True)
  return mean + kappa * std

尋找acquisition function最大的對應解，更精細化的可以去優(yōu)化一下，這里僅展示隨機采樣的方式。

def acq_max(ac, gp, y_max, bounds, random_state, n_warmup=10000):
  # 隨機采樣選擇最大值
  x_tries = np.random.RandomState(random_state).uniform(bounds[:, 0], bounds[:, 1],
                  size=(n_warmup, bounds.shape[0]))
  ys = ac(x_tries, gp=gp, y_max=y_max)
  x_max = x_tries[ys.argmax()]
  max_acq = ys.max()
  return x_max

主函數

while iteration < n_iter:
 ? ?# 更新高斯過程的后驗分布
 ? ?self.GP.fit(X, y)
 ? ?# 根據acquisition函數計算下一個試驗點
 ? ?suggestion = acq_max(
 ? ? ? ? ? ?ac=utility_function,
 ? ? ? ? ? ?gp=self.GP,
 ? ? ? ? ? ?y_max=y.max(),
 ? ? ? ? ? ?bounds=self.bounds,
 ? ? ? ? ? ?random_state=self.random_state
 ? ? ? ?)
 ? ?# 進行試驗（采樣），更新觀測點集合
 ? ?X.append(suggestion)
 ? ?y.append(target_func(suggestion))
 ? ?iteration += 1

編輯：黃飛