NTC測溫,尤其面對通過ADC轉換得到的數值時,你是否會猶豫:用什么方式更為合理地將這個ADC值轉換為溫度T?
假設我們已經對ADC的分辨率、準確度,以及所選的NTC精度范圍都有了選擇。對于絕大多數的應用而言,通過電阻分壓方式的配置就可以滿足我們所需的配置及所需的精度;個別高精度的NTC測溫會用到4線制以消除導線電阻帶來的誤差,這些暫不在我們今天討論的話題范圍。
因為提供的NTC的參數內容不一樣,本文以我們之前除霧傳感器中的測量前擋風玻璃溫度的NTC為例作為比較和說明。
查表方式的特點
查表方式的操作:二分法查找和線性插值;
通過R-T表獲取擬合NTC的R(T)特性公式;
公式計算方式的特點
對于查表和R-T公式計算方式測溫的兩種方法比較
查表方式的特點
相對的,對于測量精度要求不是太高,或者只提供了R-T表的,而且相應溫度測量范圍不是太寬情況下的應用,用查表方式一般可以解決問題。這里表內存儲的元素為int類型的ADC值,而不是其他字節數長度更多的float或者double數,否則無法達到節省代碼的目的,從而表占用的代碼空間就不會太大。當利用查表方式使用NTC測溫時,最好將制表的溫度分辨率不低于需要的測溫精度。例如,如果測溫精度要求為+/-1°C,那么表中的溫度參數間隔就至少不低于1°C;而位于表內兩個鄰近溫度值之間的數值,則采用線性插值的方式進行。
以除霧傳感器中的NTC為例。下側圖中:
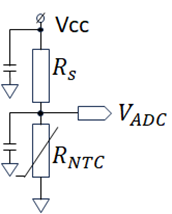
R_NTC為當前的NTC
Rs為串聯分壓電阻(9kohm)
Vcc為驅動電壓(5V)
V_ADC為12位的分壓ADC數值。
在以上這種設定情況下,我們通過使用excel可以得到像以下一樣的表格:
| TEMP(°C) | R_NTC (kohm) | Vout | ADC(12bit) |
| 0 | 27.76 | 3.757009 | 3078 |
| 1 | 26.57 | 3.716083 | 3044 |
| 2 | 25.438 | 3.674521 | 3010 |
| 3 | 24.361 | 3.632344 | 2976 |
| 4 | 23.335 | 3.589651 | 2941 |
| 5 | 22.358 | 3.546371 | 2905 |
| 6 | 21.427 | 3.502596 | 2869 |
| 7 | 20.54 | 3.458323 | 2833 |
| 8 | 19.695 | 3.41365 | 2796 |
| 9 | 18.89 | 3.368501 | 2759 |
| 10 | 18.121 | 3.323023 | 2722 |
| 11 | 17.389 | 3.277182 | 2685 |
| 12 | 16.69 | 3.230993 | 2647 |
| 13 | 16.022 | 3.184605 | 2609 |
| 14 | 15.386 | 3.13788 | 2571 |
| … | … | … | … |
這樣,通過這個表,我們就可以建立溫度和分壓電路ADC之間的映射。從表中任意兩個相鄰溫度對應的ADC值可以看到,還有許多ADC值將面對“空白”。
如果允許,一方面我們可以在兩個溫度值對應的ADC之間進行線性插值的方式進行換算;另一方面,如果允許,還可以生成更多的數值對,以實現更高的查表分辨率。
另外,如果限于所使用器件(比如MCU的代碼空間尺寸)的限制,不得不使用當前表格的分辨率,甚至需要減小表格的溫度分辨率時(比如從間隔1°C增加到2°C),如果允許,就更需要使用線性插值的方式來計算當ADC值落入中間空白值時對應的溫度,比如在上表中如果ADC=2700時,那么對應的溫度值將處于10°C和11°C之間。
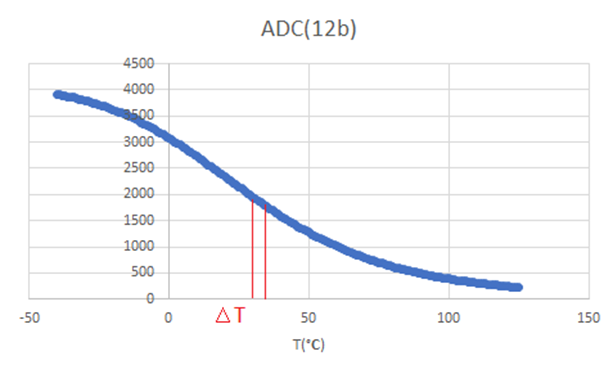
我們看一下基于分壓電路的ADC值和溫度T之間的關系圖(如下)。
再比較一下NTC的原始R-T圖(如下)。
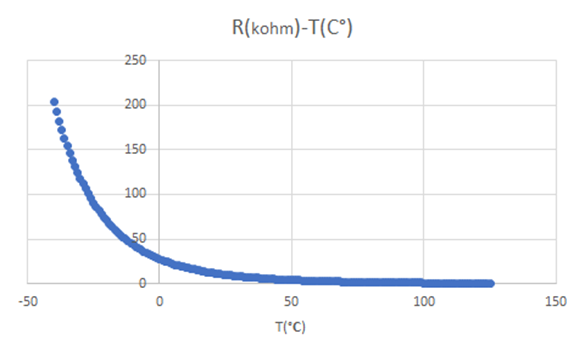
由于ADC值/T圖中的曲線更加平直,在橫軸上取溫度間隔?T很小時,對應的ADC—T曲線將非常近似于直線,這也是為什么可以在相鄰的表格溫度T與ADC值之間可以采用線性插值的理由。
查表方式的操作:二分法查找+線性插值
兩個步驟:(1)二分法找到當前ADC對應的表中索引位置;(2)線性插值計算溫度值。
相比于線性查找時間復雜度O(N),二分法查找的時間復雜度是O(LnN/Ln2),即總體上二分法所花的時間會更短。這都是在假設所查找值為一個隨機值情況下的統計。實際上由于NTC溫度探頭的響應時間的存在,或者環境溫度的平緩變化,或者ADC采集頻率的提高,那么如果程序中記錄了前一次的查找值,那么在后一次根據ADC值查找過程中,是可以將前一次的查找索引值作為參考值來處理從而縮小查找范圍的,不過在實現上會增加一些代碼。
二分法查找的python示意代碼(C和Python代碼都可以在我們網站對應文章頁面下載):
|
def binary_search(array, target): low, high = 0, len(array) - 1 while low <= high: mid = low + (high - low) // 2 mid_val = array[mid] if mid_val == target: return mid, mid elif mid_val < target: low = mid + 1 else: high = mid - 1 return high, low? |
|
if __name__ == '__main__': array = [1, 2, 4, 5, 6, 8, 11, 15, 20, 30] target = 7 low, high = binary_search(array, target) if low == high: print(f'Element {target} is at index {low}') else: print(f'Element {target} is between indexes {low} and {high}') |
上面的二分法查找代碼中有個小bug,讀者可以嘗試查找,或者在我們的網站文章頁面鏈接中下載修正之后的代碼。
以上代碼中,當low==high,即二分法查找函數返回的數組索引值相等時,此時ADC值剛好有對應表值,否則,返回值表示當前的ADC結果位于表中array [low]和array [high]兩個值之間。
當ADC的值位于表中array [low]和array [high]兩個元素值之間時,就可以考慮線性插值了。
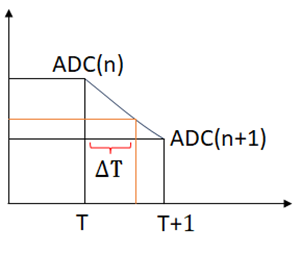
如圖,在對應的2個ADC值之間出現一個中間值ADC時(橙色線表示的坐標點為待求值,圖中溫度間隔為1℃),由于ADC(n)和ADC(n+1)之間近于直線,則根據簡單的相似原理計算出?T后就可以得出當前ADC(t)值對應的溫度值。
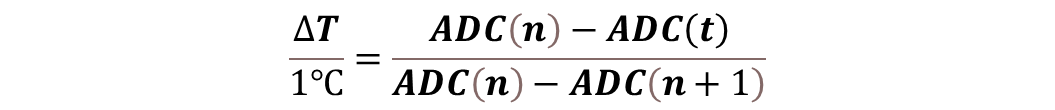
得到:
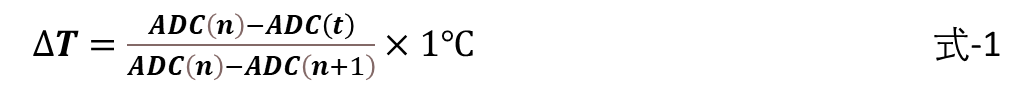
所以,ADC(t)對應的溫度值就是(T+)。這里ADC(n)和T之間存在簡單映射。讀者需要根據自己的溫度間隔設置來調整上面的公式。
在一些小型應用中,如果因為MCU的代碼空間限制問題導致無法使用更多的代碼,則可以簡單估算中間值,或者只好犧牲一些表格精度了。
可能會有人問,為什么一直在說MCU的代碼空間?如果有R-T公式,直接調用
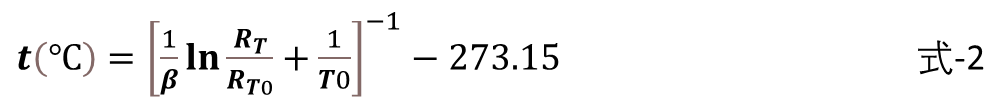
通過R-T表獲取擬合NTC的R(T)特性公式
由于手邊只有R-T表,現在考慮通過擬合的方式獲取R-T特性公式。
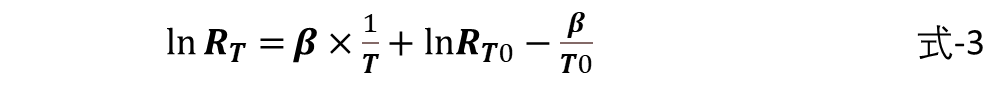
其中,T(K)=t+273.15,T0=273.15+25=298.15(K),R_To在這里也是常數,取25℃時的R值,可以從R-T表中讀取。通過處理lnR和1/T之間的線性關系,可得下圖所示的坐標圖:
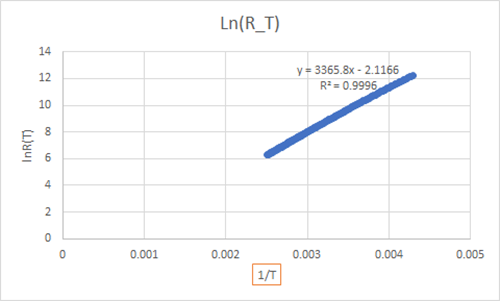
從擬合的公式中看到,可以取材料常數β=3365.8K。
余數部分經核算也基本符合,和上圖擬合公式中的2.1166相差0.04。
到這一步,[式-2]中常數項都已經得到,R-T特性公式也就定了。如果知道了NTC的當前R值,就可以根據[式-2]計算溫度值。
公式計算方式的特點
由公式計算溫度值通過以下幾步完成:
讀取分壓電路的ADC值;
通過ADC值計算NTC的R(T)值;
將R(T)值代入[式-2]計算獲取溫度值。
直接代碼如下:
|
#include floatCalWindyScreenTemp(intinputTempADC) { floatbelta = 3365.8; floatR25 = 100000.0; //float_Serial=9000.0; //floatVcc= 5.0; floatVout = 5.0 * inputTempADC/4096.0;//GetVout if(Vout>=5.0)return(-100.0);//Error indicator floatR_NTC = Vout * 90000.0/(5.0-Vout);//R_NTC floattemperature =log(R_NTC/R25)/belta + 1/(273.15+25.0); temperature = 1/temperature - 273.15; return(temperature); } |
使用公式計算似乎更為方便。不著急,我們先看一下后續的比較。
對于查表和R-T公式計算方式測溫的兩種方法比較
單從表面的代碼長度上比較的話,用公式計算的代碼要比要查表的代碼簡單得多。不過我們還是先比較一下實際編譯后的可執行代碼尺寸。
以下的數據基于STM32F103和STM32CubeIDE。
| Text | Data | Bss | Dec | 代碼內容 | 代碼變化 |
|---|---|---|---|---|---|
| 寫入到flash | 初始化后數據 | 未初始化數據 | 前三部分總和 | ||
| 3512 | 20 | 1572 | 5104 | 無NTC測溫 | |
| 5888 | 20 | 1572 | 7480 | 查表測溫 | 2376 |
| 8188 | 100 | 1884 | 10172 | 公式測溫 | 4676 |
從上面的表中可以看到,看似代碼少的公式計算法反而需要更多的代碼空間。而查表的方法(+插值運算)所需的代碼空間卻要更少些。
實際上,公式方式中單純調用log的計算所用到的函數,就會占用1~2k的字節。如果用于計算我們另外一款SC30系列高精度互換型NTC,則在額外使用指數函數(可以用連乘方式替代)的時候,代碼還會再額外增加2k字節的樣子。
所以真要比較兩種計算方法,我們可以簡單羅列如下表:
| 比較內容 | 查表插值法 | 公式法 |
|---|---|---|
| 優勢 |
一定條件下占用代碼空間小 適用已知溫度特性和測溫范圍,一個表格即可滿足應用 代碼執行速度可能會稍快,尤其在R-T表精度本身就滿足應用的情況下 在要求限制代碼尺寸的應用中可以節省成本 |
代碼編寫和調用較為方便 結果輸出直觀,計算結果基本可以直接作為最終輸出 |
| 劣勢 |
代碼編寫稍復雜 應用前需要選擇溫度范圍和精度來建表 超出表之外的溫度無法提供 |
不同溫度范圍需要不同的參數 實際代碼相比之下稍長,在限制代碼尺寸的應用中可能會增加成本 在要求運行速度的應用中可能略微慢 |
[源碼鏈接在我們網站的同名應用文檔中]
總結
應用的選擇考慮,總是成本和效能的博弈結果。窮則迂回穿插,達則全域轟炸。
關于NTC,我們在公司網站及公眾號還有其他相關的文檔可以參考。
-
傳感器
+關注
關注
2552文章
51288瀏覽量
755129 -
NTC
+關注
關注
7文章
435瀏覽量
52144 -
adc
+關注
關注
98文章
6524瀏覽量
545191 -
測溫
+關注
關注
1文章
224瀏覽量
28679
原文標題:NTC測溫—查表計算vs公式計算
文章出處:【微信號:安費諾傳感器學堂,微信公眾號:安費諾傳感器學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種基于NTC的控溫電路及軟件實現
常見的NTC類型有哪些
求助,關于NTC查表法獲得溫度的問題
計算機尋址方式解析
方法二 NTC熱敏電阻轉換溫度的計算方式

關于無線電力測溫的方式有哪些?





 NTC測溫方式之查表方式和公式計算方式
NTC測溫方式之查表方式和公式計算方式











評論