接觸檢測
步態規劃器給出的接觸序列是嚴格按照時間進行周期性計算的。而在實際運行當中,由于地形的不平整,又或者存在坡度等情況,腿部會發生提前或者延遲接觸等情況,因此只靠步態規劃器給出的接觸序列來控制機器人往往是不可靠的。
因此這里提出一個基于卡爾曼濾波的概率接觸檢測。其綜合考慮了步態規劃其給出的恒定接觸序列,足端高度,地形的不平整性,以及通過關節編碼器數據所計算出來的關節力矩,來提高接觸檢測的精度,同時減少了腿部由于電機力矩控制所引起的關節回彈現象
預測模型
卡爾曼濾波器的標準預測方程如下:

該模型有以下函數曲線:
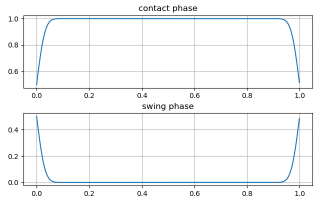
當參數(μ,σ)取不同值時,圖像如下所示,可以看出,σ取不同值時,曲線的曲率會有所變化,當曲率比較大時,其預測結果更精確,但是許用誤差范圍較小,容易造成系統的不穩定;
而當曲率變小時,預測模型的穩定性更強,其許用誤差范圍較大,但預測結果相對來說沒那么精確,實際參數的選取可根據實機結果進行調整:
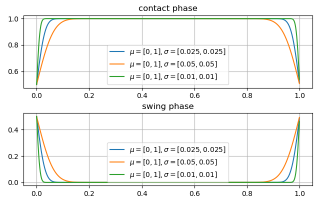
測試代碼如下:
def prediction_model(phi, state, params):
"""
Given the gait schedule and the current phase of a leg,
the gait scheduler provides an expected contact state of
each leg
:param phi: phase
:param state: contact state
:param params: [mu, mu_bar, sigma, sigma_bar]
mu = [mu1, mu2] and so on
:return: the probability of contact
"""
mu0, mu1 = params[0]
mu0_bar, mu1_bar = params[1]
sigma0, sigma1 = params[2]
sigma0_bar, sigma1_bar = params[3]
a = math.erf((phi-mu0)/(sigma0*np.sqrt(2)))
+ math.erf((mu1-phi)/(sigma1*np.sqrt(2)))
b = 2+math.erf((mu0_bar-phi)/(sigma0_bar*np.sqrt(2)))
+ math.erf((phi-mu1_bar)/(sigma1_bar*np.sqrt(2)))
if state == 1:
prob = 0.5 * (state * a)
else:
prob = 0.5 * (state * b)
return prob
因此,對于k個接觸點,該預測模型可以作為系統的瞬時輸入為:
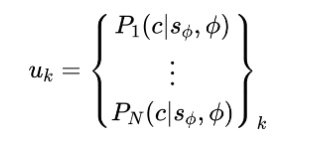
協方差矩陣如下,該矩陣表示我們對預測精度的信賴程度

由于我們只關注瞬時接觸檢測(通過融合當前可用的測量),所以狀態矩陣和輸入矩陣被定義為如下:
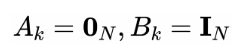
-
機器人
+關注
關注
211文章
28467瀏覽量
207353 -
檢測
+關注
關注
5文章
4492瀏覽量
91522 -
模型
+關注
關注
1文章
3254瀏覽量
48889 -
四足機器人
+關注
關注
1文章
91瀏覽量
15223
發布評論請先 登錄
相關推薦




 四足機器人接觸檢測和模型
四足機器人接觸檢測和模型










評論