總體模型
將以上兩組單獨的測量結果疊加起來,形成卡爾曼濾波器中使用的觀測向量。 同樣,每個度量的協方差矩陣形成一個整體塊 對角線協方差矩陣如下:

目前,我們使用的卡爾曼濾波用實現,這一融合過程其實可以通過貝葉斯定律的靜態似然最大化得到。
然而,上述過程是一個嵌入在標準卡爾曼更新中的過程,大概是因為在機器人學中更容易實現。
完整代碼
import math
import numpy as np
import matplotlib.pyplot as plt
# 設定周期為2
T = 2
# 根據相位計算當前接觸狀態
def get_contact_state(phi):
if phi < 0.5*T:
state = 1
else:
state = 0
return state
# 預測模型
def prediction_model(phi, state, params):
"""
Given the gait schedule and the current phase, φ, of a leg,
the gait scheduler provides an expected contact state s φ of
each leg
:param phi: phase
:param state: contact state
:param params: [mu, mu_bar, sigma, sigma_bar]
mu = [mu1, mu2] and so on
:return: the probability of contact
"""
mu0, mu1 = params[0]
mu0_bar, mu1_bar = params[1]
sigma0, sigma1 = params[2]
sigma0_bar, sigma1_bar = params[3]
a = math.erf((phi-mu0)/(sigma0*np.sqrt(2)))
+ math.erf((mu1-phi)/(sigma1*np.sqrt(2)))
b = 2+math.erf((mu0_bar-phi)/(sigma0_bar*np.sqrt(2)))
+ math.erf((phi-mu1_bar)/(sigma1_bar*np.sqrt(2)))
if state == 1:
prob = 0.5 * (state * a)
else:
prob = 0.5 * (state * b)
return prob
# 測量模型-離地高度
def ground_height(pz, params):
"""
The probability of contact given foot heigh
:param pz: ground height
:param params: [mu_z, sigma_z]
:return: The probability of contact
"""
mu_z, sigma_z = params
prob_ground_height = 0.5 * (1 + math.erf((mu_z-pz) / (sigma_z*np.sqrt(2))))
return prob_ground_height
# 測量模型-反作用力
def contact_force(f, params):
"""
the probability of contact given the estimated foot force
:param f: contact force
:param params: [mu_z, sigma_z]
:return: The probability of contact
"""
mu_f, sigma_f = params
prob_force = 0.5 * (1 + math.erf((f-mu_f) / (sigma_f*np.sqrt(2))))
return prob_force
# 概率分布繪圖
def test_predict():
Mu = [0, 1]
Mu_bar = [0, 1]
Sigma = [0.025, 0.025]
Sigma_bar = [0.025, 0.025]
t = np.linspace(0, 0.999, 1000)
prediction_prob = []
prediction_prob2 = []
prediction_prob3 = []
for time in t:
phi = time % T
state = get_contact_state(phi)
p = prediction_model(phi, state, [Mu, Mu_bar, Sigma, Sigma_bar])
p2 = prediction_model(phi, state, [Mu, Mu_bar, [0.05, 0.05], [0.05, 0.05]])
p3 = prediction_model(phi, state, [Mu, Mu_bar, [0.01, 0.01], [0.01, 0.01]])
prediction_prob.append(p)
prediction_prob2.append(p2)
prediction_prob3.append(p3)
fig = plt.figure()
plt.subplot(211)
plt.title('contact phase')
plt.grid()
plt.plot(t, prediction_prob, label='$mu=[0, 1],sigma=[0.025, 0.025]$')
plt.plot(t, prediction_prob2, label='$mu=[0, 1],sigma=[0.05, 0.05]$')
plt.plot(t, prediction_prob3, label='$mu=[0, 1],sigma=[0.01, 0.01]$')
plt.legend()
plt.subplot(212)
plt.title('swing phase')
plt.grid()
plt.plot(t, 1-np.array(prediction_prob), label='$mu=[0, 1],sigma=[0.025, 0.025]$')
plt.plot(t, 1-np.array(prediction_prob2), label='$mu=[0, 1],sigma=[0.05, 0.05]$')
plt.plot(t, 1-np.array(prediction_prob3), label='$mu=[0, 1],sigma=[0.01, 0.01]$')
plt.legend()
fig.tight_layout()
plt.show()
def test_ground_height():
height = np.linspace(-0.3, 0.3, 1000)
ground_height_prob = []
ground_height_prob2 = []
ground_height_prob3 = []
params = [0, 0.025]
params2 = [0, 0.05]
params3 = [0, 0.1]
for h in height:
ground_height_prob.append(ground_height(h, params))
ground_height_prob2.append(ground_height(h, params2))
ground_height_prob3.append(ground_height(h, params3))
fig2 = plt.figure()
plt.plot(height, ground_height_prob, label='$mu=0,sigma=0.025$')
plt.plot(height, ground_height_prob2, label='$mu=0,sigma=0.05$')
plt.plot(height, ground_height_prob3, label='$mu=0,sigma=0.1$')
fig2.tight_layout()
plt.legend()
plt.grid()
plt.show()
def test_contact_force():
force = np.linspace(-50, 200, 1000)
contact_force_prob = []
contact_force_prob2 = []
contact_force_prob3 = []
params = [35, 10]
params2 = [35, 25]
params3 = [35, 50]
for f in force:
contact_force_prob.append(contact_force(f, params))
contact_force_prob2.append(contact_force(f, params2))
contact_force_prob3.append(contact_force(f, params3))
fig3 = plt.figure()
plt.plot(force, contact_force_prob, label='$mu=25,sigma=10$')
plt.plot(force, contact_force_prob2, label='$mu=25,sigma=25$')
plt.plot(force, contact_force_prob3, label='$mu=25,sigma=50$')
fig3.tight_layout()
plt.grid()
plt.legend()
plt.show()
# test_predict()
# test_ground_height()
test_contact_force()
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
機器人
+關注
關注
211文章
28578瀏覽量
207796 -
測量
+關注
關注
10文章
4925瀏覽量
111612 -
模型
+關注
關注
1文章
3280瀏覽量
48992 -
四足機器人
+關注
關注
1文章
91瀏覽量
15231
發布評論請先 登錄
相關推薦
stm32紅外六足機器人
六足爬行機器人畢業時的作品,當時還處于入門狀態,c程序寫的比較菜(程序寫的比較亂,僅作參考),一直想把這個六足機器人作品優化一下,可惜,一直在忙,現借助電路城這個平臺開源給大家,希望大
發表于 03-27 18:51
【OK210申請】四足輪式機器人
申請理由:我正在做這樣一個機器人,遇到了很多問題,非常想學習一下這款板子!我相信利用它能幫我解決難題!項目描述:可利用四足機械結構仿生行進,也可利用車輪進行行進,集四
發表于 06-25 19:38
【Embedded Pi申請】六足機器人的創新研發
申請理由:關于六足機器人,基本上是用18個舵機一起使用來驅動六足完成相應的動作組,而一般的89C52以及STC12系列的單片機只能讓六足機器人
發表于 11-25 15:35
四足機器人的機構設計
四足機器人屬于復雜機電系統,需要綜合生物、機械、電子、控制等學科內容,具體涉及仿生機構設計、靈巧運動機構設計、高性能驅動器制造,行走穩定性控制、強化學習等在內的多個研究方向。其中,機構設計是保障
發表于 09-15 06:54
四足機器人遍地開花,四足機器人的市場有多大
幽靈公主的坐騎在現實中被造出來了? 日本川崎重工3月9日首次公開了旗下開發的全新四足機器人,外形類似宮崎駿《幽靈公主》中主角的坐騎——酷似山羊的雅酷兒。這款四




 四足機器人足端接觸檢測完整代碼
四足機器人足端接觸檢測完整代碼
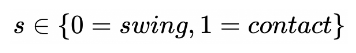










評論