導讀:文章從8個小節(jié)詳講,分為,1.關于Smith圓圖;2.等反射系數(shù)圓;3.等反射系數(shù)圓的分析;4.歸一化阻抗圓;5.電阻圓;6.電抗圓;7.完整的Smith阻抗圓圖總結;8.導納圓圖。
1.關于Smith圓圖
Smith圓圖是1939年由P.Smith在貝爾電話實驗室工作時開發(fā)的。
史密斯圓圖由兩族圓組成:等反射系數(shù)圓、歸一化阻抗圓圖。歸一化阻抗圓又包含了電阻圓、電抗圓兩種。
2.等反射系數(shù)圓
首先線上任意一點的反射系數(shù)等于下式:
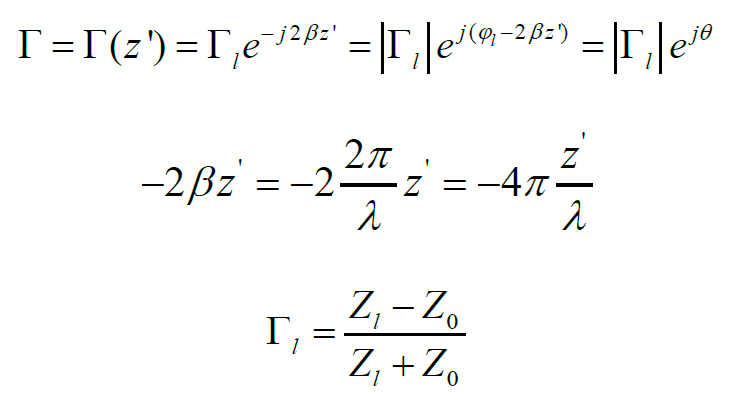
注意:典型的傳輸線系統(tǒng)如下,只要寫的是z’,表示的是從負載端為坐標起點。另外z’/λ也就是電長度。
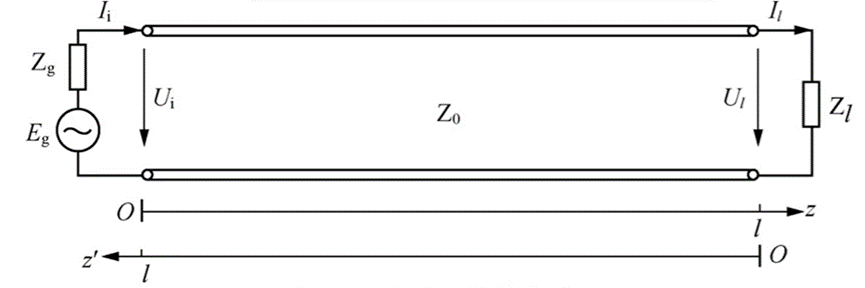
上面的反射系數(shù)式子,用實部和虛部的形式表示為:
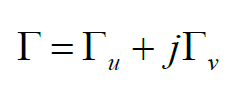
用模的形式表示,有:
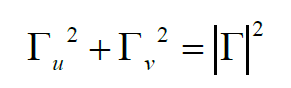
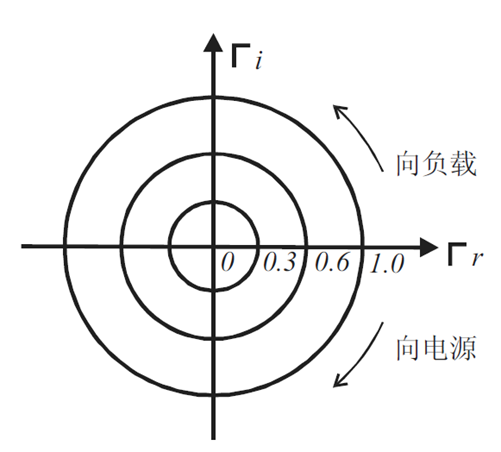
如果以Гu為橫軸(可以理解為x軸),Гv為縱軸(可以理解為y軸),畫圖,那么上式就就是以原點為圓心,反射系數(shù)的幅值|Г|為半徑的圓。這個圓就是等反射系數(shù)圓。如下圖:
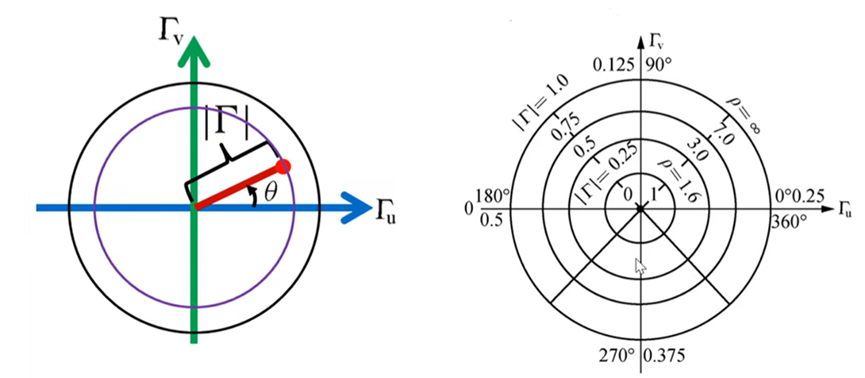
3.等反射系數(shù)圓的分析
根據(jù)反射系數(shù)的計算公式:
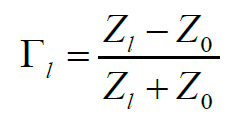
當終端短路時,即Zl=0。此時反射系數(shù)Гl就為-1。-1也就是1ejπ。所以,短路點在坐標軸中的位置為(-1,0),即實部為-1,虛部為0,在圓圖中的最左邊的一點。
當終端開路時,即Zl為無窮大,根據(jù)上式兩個相等的無窮大比值就為1。此時反射系數(shù)Гl就為1。1也就是1ej0。所以,開路點在坐標軸中的位置為(1,0),即實部為1,虛部為0,在圓圖中的最右邊的一點。
當終端接負載等于傳輸線特性阻抗(Z0=Zl),此時反射系數(shù)就為0。所匹配點在圓心(0,0)的位置。
因為反射系數(shù)的模值范圍是:0≤|Г|≤1,所以等反射系數(shù)圓是一族以原點為圓心的同心圓,最小圓的半徑為0,此處為匹配點。最大圓的半徑為1,這個圓代表著全反射。
再根據(jù)下式來分析幅角θ。θ是從坐標原點出發(fā),終止于單位圓的射線,并規(guī)定單位圓與正實軸的交點為θ=0°,從該點逆時針方向旋轉(zhuǎn)一周,θ從0°增加到360°。
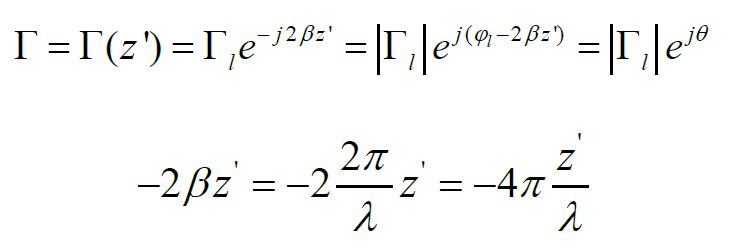
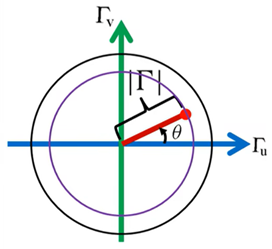
反射系數(shù)的幅角的變化與傳輸線上兩點間的電長度△z’/λ有關,因此通常可以用電長度來表示幅角。當z’=λ/4時,幅角-2βz’就等于-π。因此,半個圓周就相當于0.25λ,整個圓周相當于0.5λ。
另外,z’為正的時候,幅角θ為負數(shù),也就是順時針。注意前面說過,只要寫的是z’,表示的是從負載端為坐標起點。所以,在圓圖中順時針轉(zhuǎn)的時候,就是從負載向電源端轉(zhuǎn),逆時針就是向負載轉(zhuǎn)。
4.歸一化阻抗圓
實際的阻抗等于下式,注意Zc是特性阻抗,有時也用Z0表示,一般無耗傳輸線用Zc。
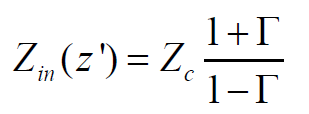
歸一化的阻抗寫成下式:
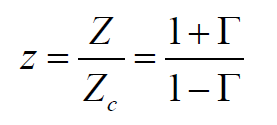
反射系數(shù)Г在前面已經(jīng)用下式表示:
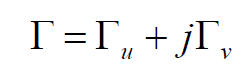
所以把上式代入到z,就可以得到z關于Гu和Гv的等式。將z也寫成實部和虛部的形式:
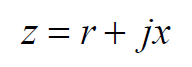
其中,把代入后得到的r和x值求出來,得到:
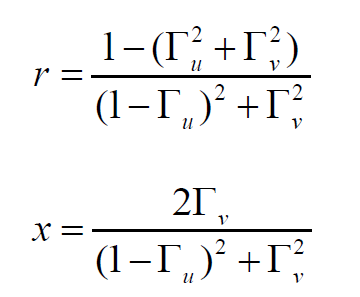
把上面兩個式子,再整理一下,就有了以下的式子:
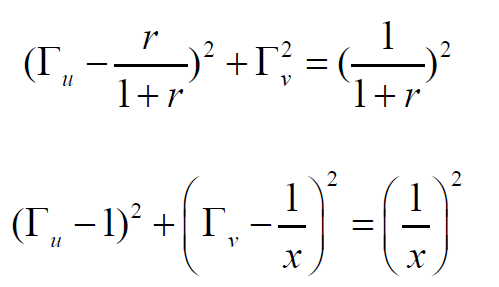
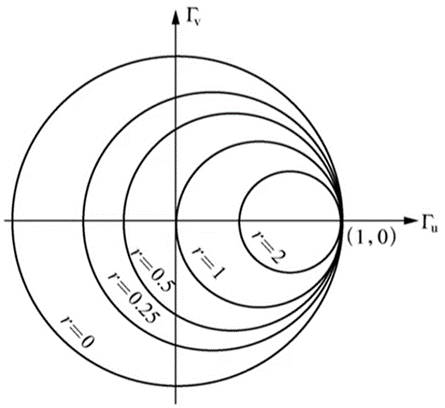
還是以Гu為橫軸,Гv為縱軸,這兩個方程都是圓的方程。畫圓,當歸一化的電阻r取不同常數(shù)時,第一個式中畫出來的一族圓,就稱為歸一化電阻圓,第二個式子畫出的圓為電抗圓。
5.電阻圓
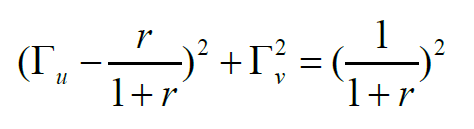
當Гu =1,Гv=0時,上式恒成立。所以不管r等于多少,這些圓都恒過(1,0)坐標點。
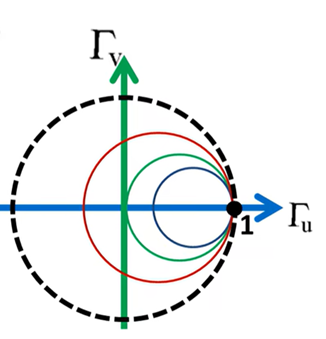
分析電阻圓的公式,圓心為(r/(1+r),0),半徑為1/(1+r)。r越大,對應的等電阻圓的半徑就越小。電阻r的范圍是0≤r<∞。
6.電抗圓
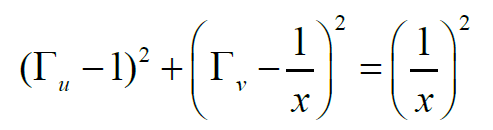
圓心為(1,1/x),半徑為1/|x|,注意電阻r不可能有負的電阻,但x可正可負。x為正,代表感性,x為負,代表容性。所以可以畫出來兩組,而且恒過(1,0)點,如下所示:
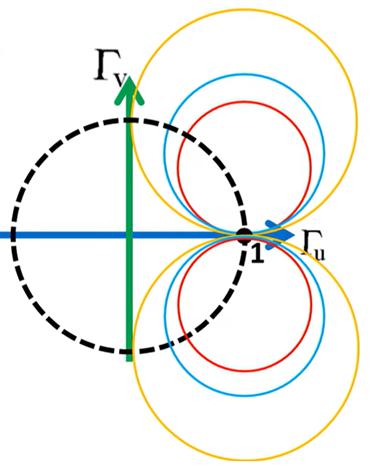
由于反射系數(shù)的限制,所以上圖彩色圓的部分只有虛線內(nèi)的才是可以用的。所以得到的電抗圓圖如下所示:
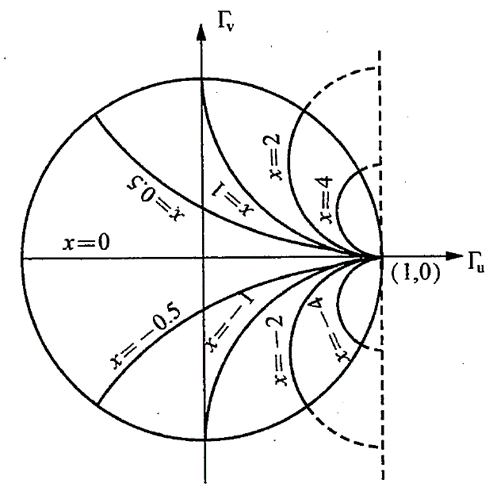
7.完整的Smith阻抗圓圖總結
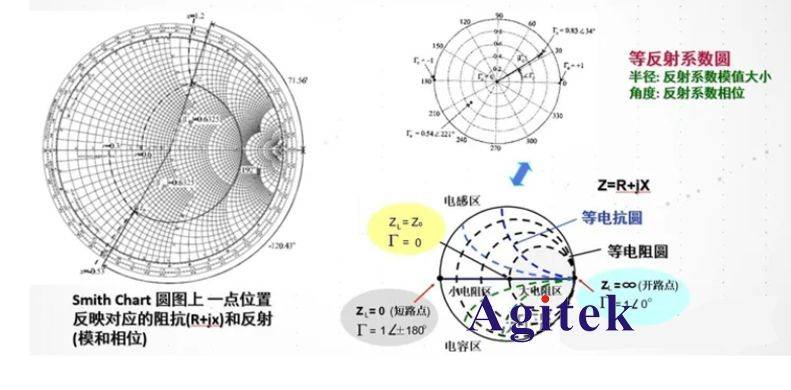
將上述的等反射系數(shù)圓、等歸一化的電阻圓、等歸一化的電抗圓重疊在一起,就構成了完成是阻抗圓圖,又稱史密斯圓圖。
根據(jù)以上對圓圖構成的分析,可以得到以下的結論:
(1)圓圖的中心點對應于Г=0,r=1(即Zl=Zc),x=0,ρ=1,是匹配點。
(2)實軸上的所有點(兩端點除外)表示為純歸一化電阻。這是因為當x等于0時,電抗圓的半徑為∞,等電抗圓退化為實軸。
(3)實軸左端點對應的Г= -1,z=0,故該點是短路點。
(4)實軸右端點對應的Г= 1,z=∞,故該點是開路點。
(5)圓圖的單位圓對應于Г= 1,r=0,z = jx,所以該圓為純歸一化電抗圓。
(6)實軸以上x>0,所以上半圓各點代表各種不同數(shù)值的感性阻抗。
(7)實軸以下x<0,所以下半圓各點代表各種不同數(shù)值的容性阻抗。
(8)圓圖的右半實軸(幅角θ=0°)上的點對應于傳輸線上電壓的同相位點,所以的電壓波腹點(電流波節(jié)點),r的值即為電壓駐波系數(shù)ρ的值。左半實軸對應電流波腹點(電壓波節(jié)點),即電流的同相位點。
(9)圓圖最外圈標有電長度的刻度,阻抗圓圖上的電尺寸刻度的起算點在實軸的左端點。圈外刻度順時針轉(zhuǎn),即“向波源方向”。逆時針轉(zhuǎn),是“向負載方向”。
(10)串聯(lián)電感:順時針沿電阻圓移動。
因為電感和電容都只影響復阻抗,所以實部電阻是不變的,仍然在恒阻圓上。同時,電感的感抗jωL為正,串聯(lián)電感,電感增大,感抗增大。由于電抗圓中,順時針的感抗是增大的(可看上面電抗圓圖中x=0.5,x=1,x=2,x=4的位置,順時針時候感抗是增大的),所以串聯(lián)電感是沿著電阻圓、順時針轉(zhuǎn)。
(11)串聯(lián)電容:逆時針沿電阻圓移動。
串聯(lián)電容,電容是減小的,容抗減小(負的更多了),所以逆時針轉(zhuǎn)。
(12)并聯(lián),一般在導納圓圖中轉(zhuǎn),具體見下文的導納圓圖。此時:
并聯(lián)電感:沿著電導圓、逆時針移動。
并聯(lián)電容:沿著電導圓、順時針移動。
8.導納圓圖
傳輸線上并聯(lián)元件或并聯(lián)分支線,用導納計算要比阻抗計算方便,用于導納計算的圓圖稱為導納圓圖。
因為導納Y是阻抗Z的倒數(shù),所以傳輸線上歸一化的導納為:
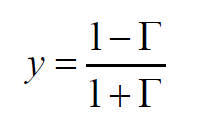
上式也可寫做:
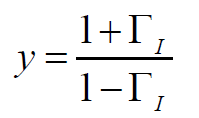
這個式子和阻抗圓圖的表達形式完全一樣,只是將原來電壓反射系數(shù)Г換成了電流反射系數(shù)ГI。因此,導納圓圖和阻抗圓圖的圖形完全相同,只是將阻抗圓圖作為導納圓圖使用時,應將阻抗圓圖中的r、x和Г相應地換位g,b和ГI。
在將阻抗圓圖作為導納圓圖使用時,因為ГI= -Г,所以原來阻抗圓圖實軸上的電壓波腹點和電壓波節(jié)點的位置,在導納圓圖實軸上分別是電壓波節(jié)點和電壓波腹點的位置。原來阻抗圓圖上的開路點和短路點的位置,在導納圓圖上對應短路點和開路點的位置。原來阻抗圓圖上的電尺寸刻度的起算點在實軸的左端點,在導納圓圖上在實軸的右端點。兩圓圖的匹配點都是左邊原點。
另外可在圓圖上由歸一化的阻抗求歸一化的導納。當位置z’=l時,阻抗和導納有下列的等式:
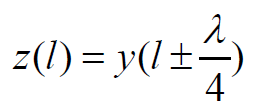
所以傳輸線上任意點z’=l處的歸一化輸入阻抗與間隔λ/4位置處的歸一化導納是相等的。所以可在阻抗圓圖上找到阻抗對應的點,沿著等反射系數(shù)圓將此點旋轉(zhuǎn)180°,相當于z’變化了λ/4,就得到了導納對應的點值。
編輯:黃飛
-
阻抗
+關注
關注
17文章
958瀏覽量
45959 -
傳輸線
+關注
關注
0文章
376瀏覽量
24034 -
串聯(lián)電感
+關注
關注
0文章
29瀏覽量
8062 -
Smith
+關注
關注
0文章
20瀏覽量
9014
原文標題:一文徹底讀懂Smith圓圖
文章出處:【微信號:射頻美學,微信公眾號:射頻美學】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
Smith圓圖是什么?Smith圓以及阻抗匹配介紹
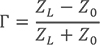




 完整的Smith阻抗圓圖總結
完整的Smith阻抗圓圖總結










評論