前文講了電子在不同能量下的分布概率,顯然概率隨能量是遵守費米分布規律連續性變化的。
至于電子在某個能量狀態下是否能夠存在,得看 是否存在對應于這個能量值的能級,并不是有出現概率就一定存在 。
回憶之前所舉的棋盤格子的例子,一個格子代表一個能級,一個能級對應一個能量。對于電子來說,一個能量可以存在兩個狀態,即兩個不同旋轉方向,也就是說,若將一個電子比喻成一個棋子,那么一個格子中能放兩個不同旋轉方向的電子。

那么要想知道電荷的濃度,相當于想要知道單位面積內的格子里有多少個電子。接下來我們將分別通過公式推導和定性的方式來解釋自發產生的電荷濃度。
電荷濃度的公式推導
01
在已知電子存在于每個格子的概率的情況下,只需要知道棋盤單位面積內總共有多少個格子即可,即用單位面積內的格子數乘以每個格子中電子的分布概率就得到總的電子數量。
上述單位面積的棋盤和格子的關系,對應到En-kn關系中,就是單位能量中的波矢數量,即dE中對應的kn數量,物理上稱為(能)態密度,即單位能量范圍內可存在的狀態密度。
顯然,對于導帶,態密度可表達為N c (E)=dX/dE,其中,dX表示在能量dE范圍內的能態數量。
導帶中電子的能量表達式為
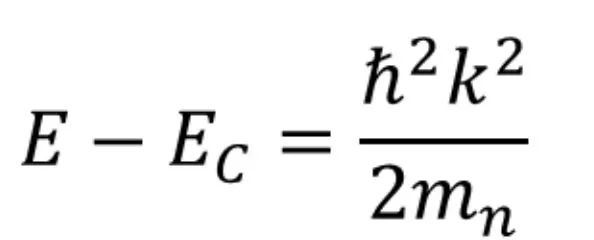

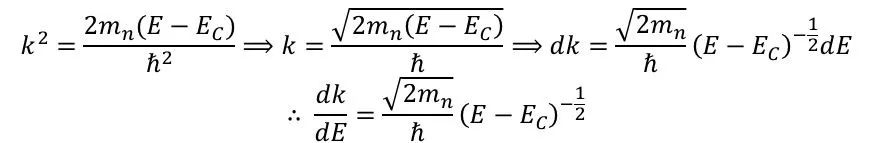
欲求得態密度dX/dE,在知道dk/dE的情況下,將其做一個變形
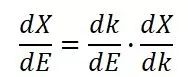

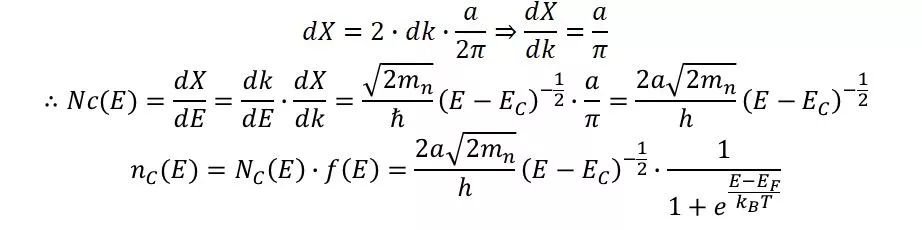
因為
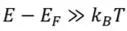 ,所以上式可以近似得到導帶中電子濃度為
,所以上式可以近似得到導帶中電子濃度為
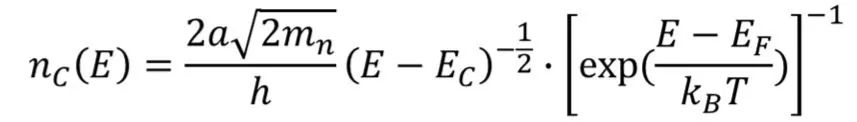
同理,可以推導出價帶中的空穴濃度,但要注意的是
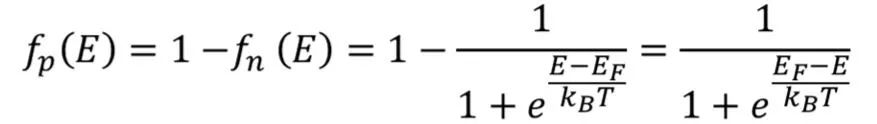
這兩個表達式即描述了在溫度T,導帶和價帶中對應某個能量本征激發的電荷濃度。
電荷濃度的定性解釋
02
電荷濃度的推導涉及到固體物理的基礎知識,盡管前文以棋盤為例進行類比,但要理解還是不大直觀,其原因主要在于E-k(能量-波矢)空間比較抽象,即倒格子空間,這是分析微觀粒子量子化特性的一個基本空間,完全是一個想象出來的數學抽象空間。
為什么需要這么一個抽象空間呢?因為微觀粒子的描述方式有一個基本方程式叫做薛定諤方程,描述了 微觀粒子的波函數和能量之間的關系,波函數表征的則是粒子出現的概率 。
如前文提到空間自由電子的波函數表達式為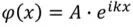
 ,k是描述波函數的重要物理量,所以在E-k所描繪的空間中,可以比較方便地推導各種微觀粒子的狀態。
,k是描述波函數的重要物理量,所以在E-k所描繪的空間中,可以比較方便地推導各種微觀粒子的狀態。
至于薛定諤方程的由來,以及如何通過薛定諤方程推導某種具體粒子的狀態,在此不做贅述。
還是結合棋盤的例子,這里再進一步做解釋,大致邏輯可以梳理如下:若將一個電子比作一枚棋子,能級比作一個棋盤上的格子,能帶比作一層又一層的棋盤。棋子有一個特性就是一直處于旋轉狀態,可以順時針旋轉,也可以逆時針旋轉,猶如圍棋中有白棋和黑棋。
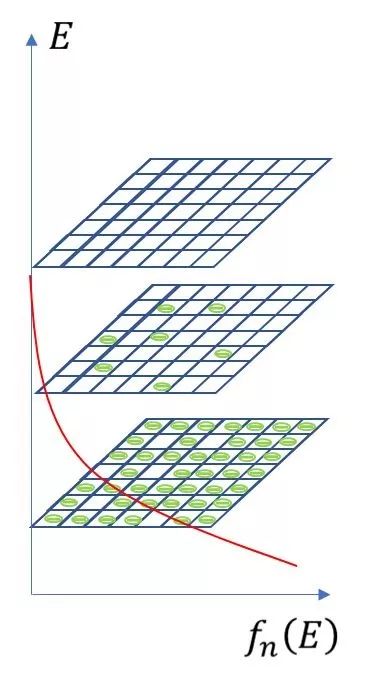
一個格子只能放一顆白棋或者一顆黑棋或者一顆白棋加上一顆黑棋,也就是說 一個能級最多只能存在兩個不同旋轉方向的電子 ,原則上棋子可以在空間中任何位置出現,包括棋盤之上以及棋盤之間的空間,其出現的規律符合費米分布。
但是只有將棋子放到棋盤之上的格子之中,才符合下棋的規則,所以并不是有出現概率就一定會出現,放入哪一層的棋盤以及棋盤中哪一個格子的概率同樣遵從費米分布,顯然某一層棋盤中能放入多少棋子(電子濃度),就看 這個棋盤中有多少格子,以及棋子放入這些格子的概率 。格子的數量和周期則與材料本身的特性相關,如原子之間的間距、質量等。
文末總結
1、通過公式推導,得出導帶中電子濃度:
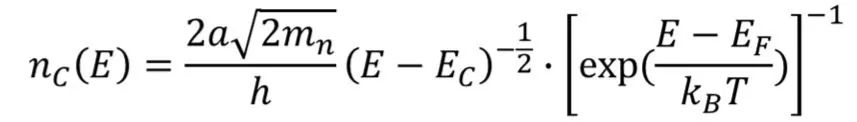
2、同理得到價帶中的空穴濃度:
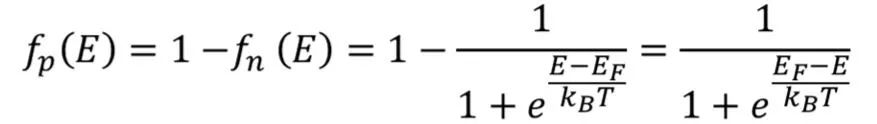
3、定性解釋:
以棋盤實驗為例,原則上棋子可以在空間中任何位置出現,但是只有將棋子放到棋盤之上的格子之中,才符合下棋的規則,所以并不是有出現概率就一定會出現,某一層棋盤中能放入多少棋子(電子濃度),就看這個棋盤中有多少格子,以及棋子放入這些格子的概率。
-
電荷
+關注
關注
1文章
642瀏覽量
36186
發布評論請先 登錄
相關推薦
電荷泵供應多少電流?
[專]電荷為何自發產生——第一彈
[專]電荷為何自發產生——第二彈
你真的懂Word嗎
壓電陶瓷傳感器的特性及工作原理解析
移動的電荷如何產生磁場
雙視圖幾何:你真的理解嗎?
自發輻射的機制是什么?為什么會自發輻射?




 你真的理解自發產生的電荷濃度嗎?
你真的理解自發產生的電荷濃度嗎?










評論