圖像處理領域中涉及很多特征，角點特征，邊緣特征，形狀特征，紋理特征，顏色特征，直方圖統計特征等等（還有很多^_^）。這些特征有些是比較底層的特征，如角點特征，邊緣特征，顏色特征等，有些則是較為高層的特征，如形狀特征，紋理特征，直方圖統計特征。

這里我們主要談論底層特征中的邊緣特征，提取這些特征的手段叫作邊緣特征提取或叫作邊緣檢測。邊緣檢測常用的算子中分為一階檢測算子和二階檢測算子，這里提及的算子有些類似數學中的微分的概念（要有一定的數學基礎哦）。邊緣檢測的另外一種形式也被成為相位一致性，這個概念我到后面再談及，有了這個概念之后幫助我們從圖像頻域分析邊緣提取這一過程。

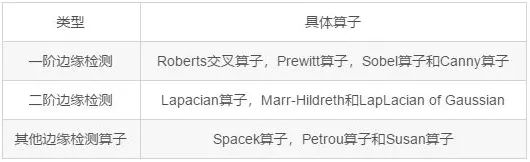
表1 圖像處理邊緣檢測算子分類表格

基于邊緣檢測的分析不易受整體光照強度變化的影響，同時利用邊緣信息容易凸顯目標信息和達到簡化處理的目的，因此很多圖像理解方法都以邊緣為基礎。邊緣檢測強調的是圖像對比度。對比度從直觀上的理解就是差異的大小，若對于灰度圖像來說就是灰度值（亮度值）的差別，若對于彩色圖像則是顏色的差異了。這些差異可以增強圖像中的邊界特征，因為這些邊界就是圖像對比度較大的體現。

這就是我們感知目標邊界的大體機制，因為目標的表現就是與它周圍的亮度差別。

一、水平差分算子、垂直差分算子

亮度變化可以通過對相鄰點進行差分處理來增強。對水平方向的相鄰點進行差分處理可以檢測垂直方向上的亮度變化，根據其作用通常被稱為水平邊緣檢測算子（horizontal edge detector），這樣就可以檢測出垂直邊緣Ex；對垂直方向的相鄰點進行差分處理可以檢測水平方向上的亮度變化，根據其作用通常被稱為垂直邊緣檢測算子（vertical edge detector），這樣就可以檢測出水平邊緣Ey。

Ex = |Px,y - Px+1,y|
Ey = |Px,y - Px,y+1|

將水平邊緣檢測算子和垂直邊緣檢測算子結合，就可以同時檢測出垂直邊緣和水平邊緣，即：

Ex,y =|Px,y - Px+1,y + Px,y - Px,y+1|

由此可以得到

Ex,y =|2 x Px,y - Px+1,y - Px,y+1|

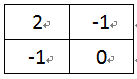
圖1 一階差分模板

利用泰勒級數分析可以知道相鄰兩點的差值是一階導數的估算值，誤差。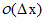
如果在相鄰兩個差分點之間插入一個像素來實現，相當于，相當于用兩個相鄰點的一階差分作為新的水平差值Exx，其中

Exxx,y = Ex x+1,y + Ex x,y = |Px+1,y - Px,y + Px,y - Px-1,y| = |Px+1,y - Px-1,y |

利用泰勒級數分析可以知道一階微分的估算值是由一個像素隔開的兩個點的差值，誤差。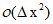

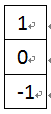
圖2-1 改進的一階差分模板My

圖2-2 改進的一階差分模板Mx

二、一階邊緣檢測

(a) Roberts交叉算子

Roberts交叉算子實現的基礎是一階邊緣檢測，利用兩個模板，計算對角線上而不是坐標軸上的兩個像素的微分。這里命名這兩個模板分別為M+,M-

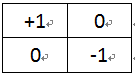
圖3-1 Roberts交叉算子模板M+

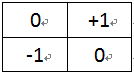
圖3-2Roberts交叉算子模板 M-

(b) Prewitt邊緣檢測算子

邊緣檢測類似微分處理，它檢測的變化的部分，必然對噪聲和圖像的亮度變化都有相應處理。因此，把均值處理加入到邊緣檢測過程中一定要非常謹慎。我們可以把垂直模板Mx擴展成三行，而水平模板My擴展成三列。這樣就得到Prewitt邊緣檢測算子。

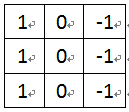
圖4-1 Prewitt算子模板Mx

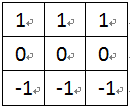
圖4-2 Prewitt算子模板My

(c) Sobel邊緣檢測算子

如果把使兩個Prewitt模板算子中心像素的權值去兩倍的數值，便得到有名的Sobel邊緣檢測算子，它是由矢量方式確定邊緣的兩個掩碼組成的。Sobel很受歡迎是因為它比Prewitt算子等同時期的其他邊緣檢測算子性能更好。

圖5-1 Sobel算子模板Mx

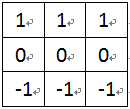
圖5-2 Sobel算子模板My

Sobel算子的通用形式綜合了一條坐標軸上的最優平滑和另一條坐標軸上的最優差分。值得注意的是，大的邊緣檢測模板的好處是它減少噪聲的平滑效果更好，然而邊緣模糊卻成為一個大難題。

(d) Canny邊緣檢測算子

Canny邊緣檢測算子可以說是當前最受歡迎的邊緣檢測方法。它由三個主要目標形成：

無附加響應的最優檢測

檢測邊緣位置和實際邊緣位置之間距離最小的正確定位

減少單邊緣的多重響應而得到單響應

Canny指出高斯算子對圖像平滑處理是最優的。Canny邊緣檢測一般處理的步驟可以粗略的分為以下四個步驟：

應用高斯平滑處理

應用Sobel算子

應用非極大值抑制（非極大值抑制實質上是找到邊緣強度數據中的最高點）

滯后閾值處理來連接邊緣點（閾值處理需要兩個閾值，即上限閾值和下限閾值 ）

三、二階邊緣檢測

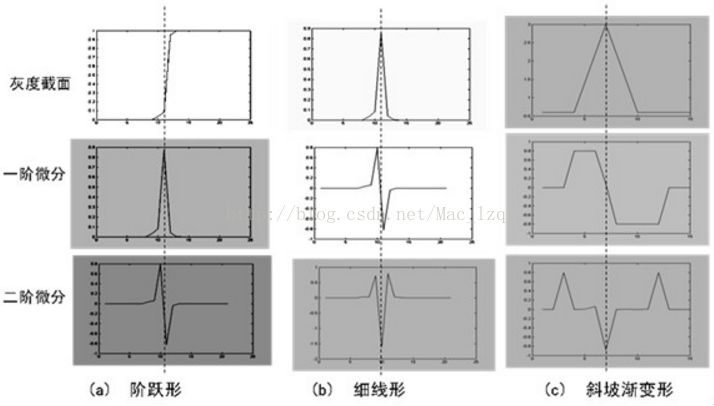
一階邊緣檢測的前提是微分處理可以使變化增強。找圖像變化率最大的地方不僅可以通過一階變化率的極值尋找，同時也可以通過二階變化的過零點來尋找。

(a) Laplacian算子

二階微分可以利用兩個相鄰一階微分的差值來近似。這也和數學中的概念相一致。

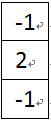
圖6-1 垂直二階模板

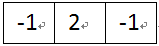
圖6-2水平二階模板

如果把水平二階算子和處置二階微分算子結合起來，可以得到一個全Laplacian模板算子。

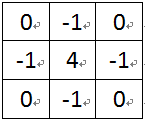
圖7 Laplacian邊緣檢測算子

(b) Marr-Hidreth算子

Marr-Hidreth也是利用高斯濾波。該算子的曲面圖是墨西哥帽子的形狀，所以有時也被成為“墨西哥帽子”算子，如下圖所示。

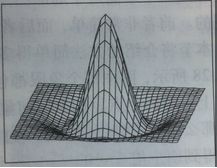
圖 8 LoG算子的形狀

實際上，如果把高斯平滑和Laplacian算子結合起來，可以得到一個LoG（Laplacian of Gaussian）算子，它就是Marr-Hidreth的基。

各算子的效果比較：

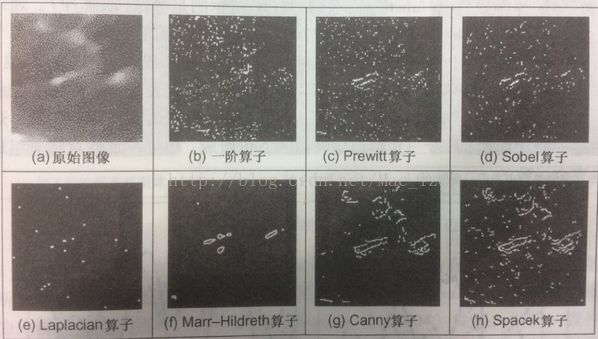
圖 8 LoG算子的形狀

四、其他邊緣檢測

邊緣檢測作為視覺處理的初級階段，方法有很多種，這里我們再提及兩個設計最優的邊緣檢測方法，Spacelk方法和Petrou方法。有興趣的朋友可以進一步了解。這里需要提及的是Spacek算子使定位信噪比和峰值分離比的乘積最大化。Spacek算子比Canny算子具有很高的性能。Petrou算子使用的模板比較大，以便保存最優性，因此Petrou算子可以處理比較大的計算復雜度，但在使用的時候，應當具體問題具體分析。

五、相位一致性

邊緣檢測算子的比較突出了它們的一些內在問題：不完整輪廓問題、閾值選擇問題和噪聲響應問題。因為光照強度在圖像的不同區域是不一樣的，選擇單個閾值通常不能適用于圖像中的所有區域。這些問題單靠簡單初級的處理難以解決。需要優化方法或者使用較為高級的手段才能達到一定的效果。

相位一致性（Phase congruency）方法是一個特征檢測算子，它由如下兩個優點：

可以檢測大范圍的特征

對局部（和平滑）光照變化具有不變性

這兩個優點其實就是一致性檢測具有局部對比度不變性：即使階梯邊緣強度變小，其變化位置并不改變。