現在我們把時間變量 加入,進行電荷總量
加入,進行電荷總量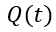 的瞬態分析。
的瞬態分析。
當柵極電壓低于閾值電壓,IGBT內部存儲的電荷開始衰減,衰減過程是因為載流子壽命有限而自然復合,表達式如下:
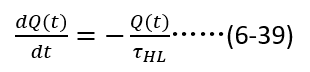
需要注意的是,在求解(6-39)的過程中,不能直接將(6-38)作為初始值,因為在關斷的一瞬間,溝道電流的突然消失,即上一節中 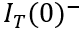 到
到 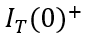 的變化,會導致IGBT體內電荷的突然減小,將電荷初始值記為
的變化,會導致IGBT體內電荷的突然減小,將電荷初始值記為 ,顯然
,顯然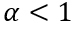 。
。 的具體數值取決于關斷之前
的具體數值取決于關斷之前 的大小,感興趣的讀者可以自行推導,這里不再贅述。(6-39)很容易積分求解,
的大小,感興趣的讀者可以自行推導,這里不再贅述。(6-39)很容易積分求解, 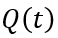 隨時間
隨時間 成e指數關系衰減,即
成e指數關系衰減,即

例如,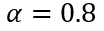 ,假設在
,假設在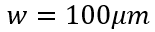 且保持不變的情況(關斷過程顯然不是這樣,下面會再討論
且保持不變的情況(關斷過程顯然不是這樣,下面會再討論 隨時間變化)存儲電荷衰減隨載流子壽命變化的衰減趨勢如圖所示。
隨時間變化)存儲電荷衰減隨載流子壽命變化的衰減趨勢如圖所示。

顯然,隨著載流子壽命的減少,電荷衰減速度加快。因為電流表征了電荷隨時間的變化率(電荷的時間微分),利用(6-39)和(6-40),乘以系數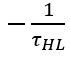 ,也就得到瞬態中電流隨時間的變化關系。
,也就得到瞬態中電流隨時間的變化關系。
在上一節中,我們定性地說明了在關斷瞬間 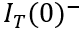 和
和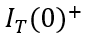 的突變,這里我們推導一下理論上這個變化究竟是多大。
的突變,這里我們推導一下理論上這個變化究竟是多大。
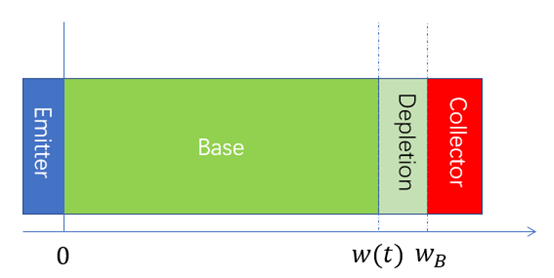
在關斷瞬間,溝道夾斷,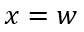 處的電子電流
處的電子電流 ,根據上一章的穩態分析中對電子電流和空穴電流與總電流的關系,參考(6-6)式,
,根據上一章的穩態分析中對電子電流和空穴電流與總電流的關系,參考(6-6)式,

此時多余載流子空穴的分布不變,參考(6-10),

可以計算得到(6-41)第二項的微分表達式,即
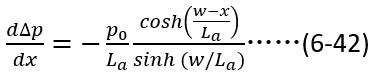
同時,很容易推導雙極性擴散長度與空穴擴散長度之間的關系如下(過程省去,讀者可以自行推導),
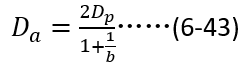
將(6-42)和(6-43)帶入(6-41),就可以得到關斷瞬間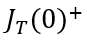 與
與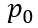 之間的關系為(令
之間的關系為(令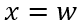 ),
),
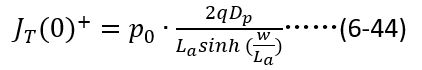
接下來,只需將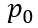 和
和 的關系帶入(6-44),即可得出
的關系帶入(6-44),即可得出 和
和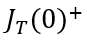 的關系。
的關系。
引用穩態分析中(6-11),即為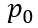 和
和 的關系,因為在這一瞬間,內多余載流子濃度分布并不會發生變化,即,
的關系,因為在這一瞬間,內多余載流子濃度分布并不會發生變化,即,
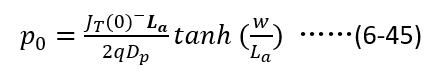
將(6-45)帶入(6-44),即得到,

根據(6-46),關斷瞬間電流突變的幅度取決于芯片厚度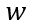 和擴散長度
和擴散長度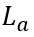 ,后者又取決于遷移率和載流子壽命。
,后者又取決于遷移率和載流子壽命。
令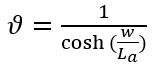 ,電流突變率,
,電流突變率,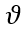 隨芯片厚度
隨芯片厚度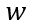 、遷移率
、遷移率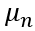 和載流子壽命
和載流子壽命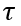 的變化趨勢如下圖所示:
的變化趨勢如下圖所示:

-
IGBT
+關注
關注
1267文章
3799瀏覽量
249194 -
電流突變
+關注
關注
0文章
3瀏覽量
6051 -
載流子
+關注
關注
0文章
134瀏覽量
7664 -
閾值電壓
+關注
關注
0文章
73瀏覽量
51445
發布評論請先 登錄
相關推薦
IGBT失效的原因與IGBT保護方法分析
大功率IGBT驅動的技術特點及發展趨勢分析
討論一下IGBT的關斷過程
IGBT增大門極電阻,關斷尖峰會增加是怎么回事呢?
關于對IGBT關斷過程的分析

IGBT關斷時的電流和電壓

米勒電容對IGBT關斷時間的影響
igbt怎樣導通和關斷?igbt的導通和關斷條件
IGBT關斷過程分析
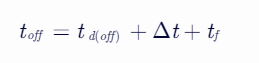




 IGBT的關斷瞬態分析—電荷存儲變化趨勢(1)
IGBT的關斷瞬態分析—電荷存儲變化趨勢(1)
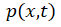
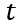
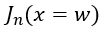
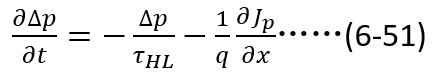










評論